 Water Dynamics Following Treatment by One Hour 0.16 Tesla Static Magnetic Fields Depend on Exposure Volume
Water Dynamics Following Treatment by One Hour 0.16 Tesla Static Magnetic Fields Depend on Exposure Volume
Gang N1,2, St-Pierre LS2 and Persinger MA1,2,3*
1Department of Biology, Laurentian University, Sudbury, Ontario, Canada, P3E 2C6
2Behavioural Neuroscience Program, Laurentian University, Sudbury, Ontario, Canada
3Biomolecular Sciences Program, Laurentian University, Sudbury, Ontario, Canada
* Correspondence: E-mail: [email protected]
Key Words: Water; static magnetic fields; diffusion, viscosity; biological systems; energy in a magnetic field
Received August 5th, 2011; Accepted October 7th, 2011; Published March 10th 2012; Available online March 18th 2012
Summary
Different volumes (25, 50, 100 cc) of spring water were exposed to either (160 mT, 1600 G) static magnetic fields, time-varying 7 Hz, 140 nT or 400 nT magnetic fields, or sham conditions for one hour. During the subsequent hours diffusion velocities for 6 µL aliquots of a solute (India ink) in 80 µL of water were then measured every 15 minutes. A sudden and protracted increase by a factor of two in diffusion velocity as a function of the exposed volume was conspicuous only for water treated by the static 1600 G magnetic field. The results are congruent with the quantified estimates of energy stored within water, the increased viscosity at the boundary of interfacial and bulk water as described by Del Giudice et al. (2010) and the dissipation of organization between hydronium atoms. This effect may lead to a simple, reliable experimental model to study “water memory.”
Article Outline
Introduction
Water is a unique molecule that has been recognized as the matrices for the chemical reactions associated with life (Del Giudice et al., 2010, Pollack et al, 2009) and is resonant with a multitude of external factors (DeMeo, 2011). Rather than being a static homogeneous medium, a volume of water molecules displays temporal and spatial variations that range from the picosecond durations of the hydronium (H3O+) atom (DeCoursey, 2003) to ephemeral compartments of molecules that oscillate synchronously (Preparta, 1995). Coherence domains span within biological space (100 nanometers) involve millions of molecules. These domains in addition to the special properties of interfacial water near surfaces (the exclusion zone) where solutes were less probable to penetrate may be more responsible for the conditions of life than expected (Del Giudice et al., 2010). The physical properties of water (within this zone) include: 1) a ten-fold increase in viscosity relative to normal water, 2) negative electric potentials up to 150 mV, and, 3) concentrations of protons (H+) at the boundary between the zone and bulk water (Zheng et al., 2006). Such physical boundaries that display capacitor-like properties might generate conditions that allow the “representation” or “storage” of information, that is “memory”.
Recently we (Gang and Persinger, 2011) observed a strong (0.95) correlation between the swimming velocity of planarian that had been exposed for one hour per day to static magnetic fields over a range of intensities between 16 G and 1600 G with the diffusion velocities of quantized ink droplets within water that had been exposed for a comparable time to matched field strengths. However, the change in solute dispersion times as a function of volume of water exposed to the magnetic field was an unexpected observation. This finding suggested that the direct effects of magnetic fields on water were quantifiable, and that traditional concepts of “clustered water” (Pan et al., 2004) and its “memory-holding” properties might be studied systematically.
One potential parameter that could affect solute diffusion rates might involve the viscosity (8.9 x 10-4 Pa∙s) of water (Bett and Cappi, 1965). According to Fahidy (2002) diminished viscosity of 3.5% was associated with current density of 370 A/m, equivalent to magnetic field strengths of 5.9 x 10-4 T or 59 G, which was within the range of the strengths employed in our study (Gang and Persinger, 2011). For a 1.6 x 10-1 T (1600 G) magnetic field, selected in our studies for convenience, the proportional linear change would be about 95%. Another related possibility might involve the dissipation of any magnetic energy within the major mobile component of water: the hydronium atom (DeCoursey, 2003) that might be sequestered in the putative exclusion zones (Del Giudice et al, 2010).
Energy from a static magnetic field can be expressed as J=[(B2)/2∙µo]∙volume, where B is the strength of the applied field and µo is magnetic permeability (4ω x 10-7 N/A2) of free space (Walker, 2004). In a volume of 1000 cc (1.0 L, 1.0 x 10-3 m3), the stored energy from a 1600 G (0.16 T) magnetic field would be approximately 10 J. Avogadro’s number states that there are 6.023 x 1023 molecules within 1 Mole. With 110 Moles of H+ per litre of water (DeCoursey, 2003), this would equate to ~ 6.63 x 1025 hydrogen ion molecules in 1 L of water. With 4 x 10-8 M of free protons carried by hydronium (H3O+) atoms in a physiological-like condition (DeCoursey, 2003), we estimated that ~2.65 x 1018 hydronium molecules possess an average energy of about 3.8 x 10-18 J/mol. However if the excited state involved with coherent oscillation in a domain is 12.06 eV, just below the ionization threshold of 12.60 eV of the molecule, as indicated by Del Giudice et al (2010), the energy acting on a charged particle (1.6 x 10-19 A∙s) across 1 V would be in the order of 2 x 10-18 J. These estimates suggest that exposure to a magnetic field could allow for energy accumulation additional to that already present within a given quantity of water (Smith, 2004).
In the presented study we pursued the potential “storing” of energy from one hour exposures to a 1600 G static magnetic field upon different volumes of water. We assumed that changes in solvent diffusion reflected altered viscosity, although this was not the only possible explanation. Our assumption was that the sudden and protracted increased diffusion velocity would reflect the dissipation of stored energy or information. Correspondingly, if we assume the dissipation of total stored energy to be involved with altered viscosity, then larger volumes of water should show longer intervals of storage duration. The simplest prediction of the time required for this change was estimated to be the product of the moles (M) of water, molecules per mole (6.023 x 1023), free protons carried by hydronium atoms (4 x 10-8 M), and the life time of a hydronium atom (~10-12 s), with values referenced from DeCoursey (2003). For volumes of 25 cc to 100 cc these values would between 1 x 104 and 3 x 104 seconds (about 4 to 9 hours). If we assume approximately “one-third” of the water as compartmentalized (Preparta, 1995) at any given time then the “relaxation time” would be about three times these values. Here we present experimental evidence for potential support of this concept.
Materials and Methods
Static Magnetic Field Water Treatments
Static magnetic field treatment to water was delivered via a Raytheon horseshoe magnet with the strength of 1600 Gauss (1.6 x 10-1 Tesla). Each magnetic pole surface area was 13.0 cm2 and the poles were separated by a distance of 5.2 cm. Magnetic intensity was measured by a model GM1A gaussmeter from Applied Magnetics Laboratory Inc. The 1600 Gauss field intensity corresponded to a distance of approximately 0.3 cm from the magnet to the leading edge of the water container.
Spring water was obtained from Feversham, Grey County, Ontario. Ion content of the water in ppm was: HCO3 270, Ca 71, Mg 25, SO4 5.9, Cl 2.7, NO3 2.6, and Na 1. Water had received treatment by ozonation. In three separate blocks of experiments (9 separate days), three water volumes (25 mL, 50 mL and 100 mL) were treated with the North pole of the magnet for 60 minutes. Treatment occurred while the water was housed in cylindrical glass containers, sold for use as food storage, with a diameter of 3.7 cm. Water samples of 100 mL were housed in larger food-grade glass jars of a 6.0 cm diameter. Magnetic pole height was 5 cm and width 2.5 cm. There was a 1 cm discontinuity between the table surface and the bottom edge of the magnetic pole. Water volumes were of the heights 2.3 cm, 4.7 cm and 3.5 cm for the volumes 25 mL, 50 mL, and 100 mL, respectively. Consequently, approximately 25.5%, 36% and 12.3% of the water samples within the 25 mL, 50 mL, and 100 mL containers, respectively, received direct magnetic field exposure within the cross-sectional area of the pole (Figure 1).
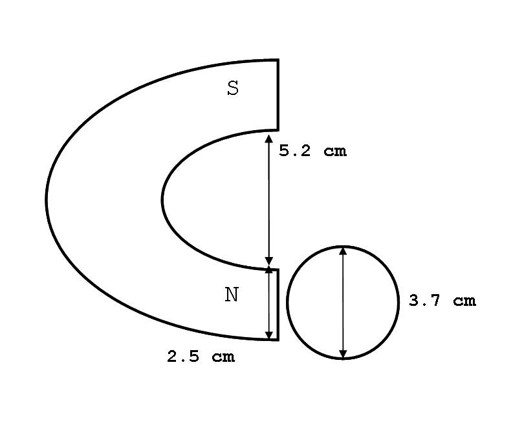
Figure 1: Diagram of the comparable lengths between the static magnetic field delivery and water container.
Following 60 minutes of magnetic field exposure, water samples were removed from the treatment position. Manual measurements of diffusion were made at 15 minute intervals for up to 10 hours. Diffusion measurements were made in serial .08 cc (80 µL) aliquots of water removed from the treated water sample. A plastic pipette removed the water to be tested to a transparent polyethylene terephthalate (PETE) trough laid over a 1 mm by 1 mm grid. The treated water aliquot was applied to the fold of the trough to cover an area of 10 mm by 3 mm (30 mm2) which required a volume of roughly 80 µL (height of 3 mm) in order to maintain shape with surface tension.
A 6 μL droplet of Artist’s Choice India ink, diluted 1:15 in untreated spring water, was then added to the edge of the treated water sample using a 100 μL Hamilton needle which was used first to break surface tension of the treated water before the ink dilution was added to that edge of the treated water (Figure 2). Diffusion velocity (mm/s) was calculated for the ink to diffuse a linear distance of 10 mm. This linear diffusion time which was conspicuous to independent observers was determined visually with a stopwatch. Five measures were made every 15 minutes for up to ten hours for each of the 9 runs that were completed on separate days from December 2010 to April 2011. Ambient temperature within the room was about 25˚C.
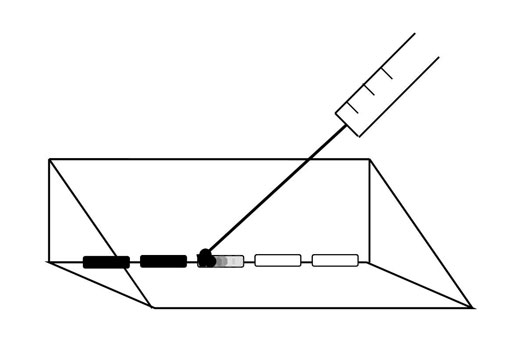
Figure 2: Schematic of ink droplets (6 µL) introduced to water aliquots removed from treated water sample. Ink was introduced via a Hamilton 100 µL syringe.
Time-varying Magnetic Field Water Treatment
In this experiment all volumes were 50 mL of Spring water. The water, contained in uncovered food-grade glass jars of the same dimensions as mentioned above, was placed in a Helmholtz coil (30 ohms, 20 AWG wire) with dimensions 41.2 cm (length) 32.5 cm (width) 32.4 cm (height). The electromagnetic pattern was produced through a custom made digital-to-analogue converter (DAC). The patterned values were controlled via a Zenith ZF 148-42 (Intel 8008 16 bit CPU with 4.7 or 8 MHz operation) computer operating with custom made software (Complex-2). 5,072 points, each with duration of 69 ms (5.8 minutes), composed the patterned field. The amplitude of this 7 Hz (Schumann resonance modeled) square wave magnetic field ranged from 0 nT to either 140 nT (weak intensity condition) or 400 nT (high intensity condition). The magnetic field was presented for 5 minutes and 50 seconds in order to simulate conditions associated with regeneration in planarian (Gang and Persinger, 2011). A figure of the wave form and coil description has been previously published (Cook et al., 2000).
The wave form was modeled after sudden-commencement geomagnetic storms and was shaped by sequential steps seven times during the first 3 minutes and 20 seconds and again during the remaining 1 minute and 42 seconds. Each plateau lasted for 14 seconds during the first cluster and for 7 seconds during the last cluster. Amplitude modulation frequency was therefore between 36 mHz and 71 mHz. The presence of field was verified by a RadioShack miniamplifier (input sensitivity: 1 mV, input impedance: 5 K Ohms) coupled to a standardized magnetic sensor.
Statistical Analyses
Means and standard errors of the mean (SEM) for each of the 15 minute measurement periods over the total time (up to 10 hours) for the three runs of each condition (volume modulated static magnetic field treatments and intensity modulated alternating magnetic field treatments), were calculated by SPSS 16 (PC) software. A protracted increase in diffusion for more than two successive 15 minute periods was considered statistically significant if there were no overlaps in the SEMs.
To discern if the treatments affected the observed periodicity of the changes in diffusion velocity of the water, spectral analyses (SPECT) were completed as well (SPSS 16). The average and standard deviations of the spectral values for each of three runs per treatment were calculated. The relative amplitudes for each frequency were then compared by discerning which spectral intervals involved no overlap in the standard deviations for the means of any two groups. The criterion for standard deviation rather than SEMs was to insure the rigor of the effect.
Results
The results were very conspicuous. The means and standard errors of the mean for diffusion velocities as a function of the static magnetic field treatment in the 25 cc, 50 cc, or 100 cc water volumes are shown in Figure 3. There was a clear increase in latency, as a function of volume of exposure, before the sudden and protracted doubling in diffusion velocities occurred. According to our criteria of two successive non-overlapping intervals, the time elapsed before diffusion speed change for the 25, 50, and 100 cc volumes were 21,150 s (5.9 hr), 26,550 s (7.4 hr) and 31,050 s (8.6 hr), respectively. There was no change in the diffusion velocities for the control (sham field) water.
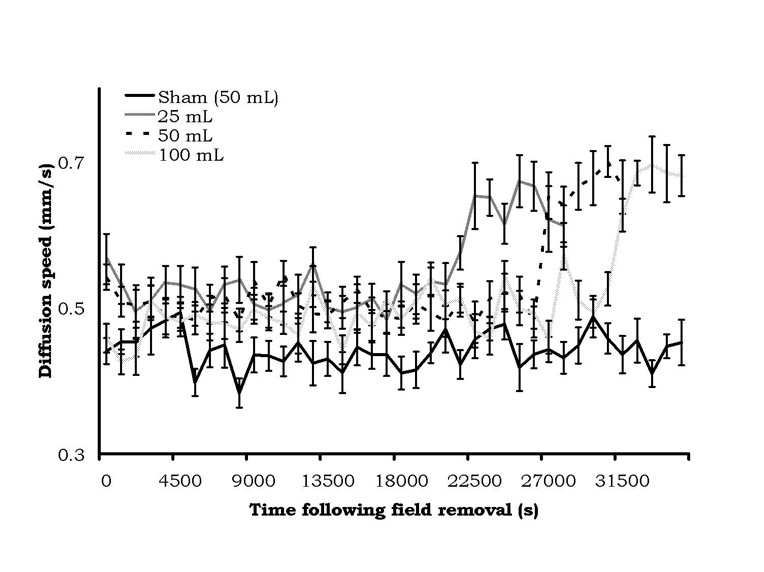
Figure 3: Diffusion velocity (mean ± SEM) from samples of water from different volumes after being treated by a static magnetic field (1600 G). Change in diffusion velocity was volume-dependent.
The results of the 6 minute alternating field exposure are shown in Figure 4. There were no criterion differences between the sham exposures within the coil and exposures to either the 140 nT or 400 nT fields. In fact, the absolute values of the diffusion velocities were within the same range as the sham conditions for the static magnetic field experiment.
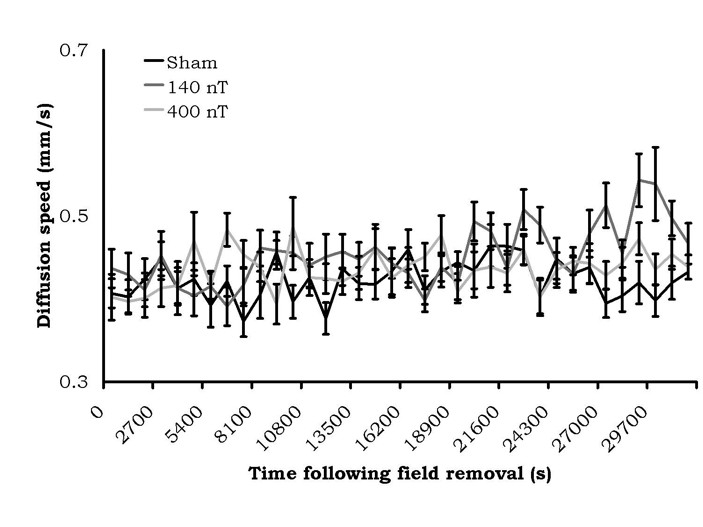
Figure 4: Diffusion velocities (mean ± SEM) of water (from a 50 mL volume) after treatment by a 7 Hz amplitude-modulated magnetic field of variable intensity. No sustained diffusion speed changes were present.
The most consistent differences in the relative amplitudes of the spectral analyses for diffusion velocities for the different volumes of water after exposures to the static magnetic field strengths or the 7 Hz, amplitude-modulated fields occurred over successive 15 minute intervals equivalent to a period between 73 and 76 minutes. The means and standard deviations for the relative power within this range are shown in Figure 5. Only the water within the 50 and 100 cc volumes showed the criterion (no overlap of standard deviations) dampening of the oscillation whereas the others did not.
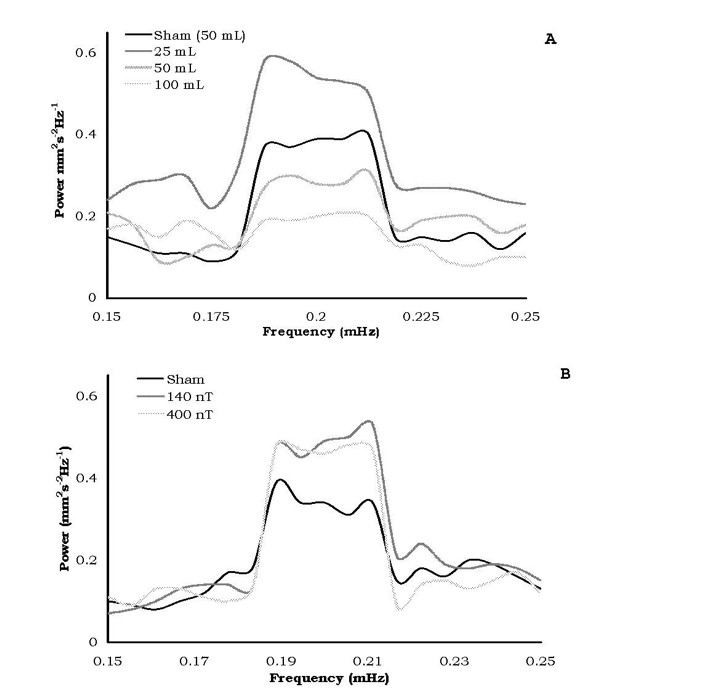
Figure 5: Spectral power amplitudes following exposures to either the static (A) or time-varying (B) magnetic field treated waters. Only the 50c and 100 cc of static field treated waters displayed criterion damping of oscillation.
Discussion
The results of this study support the quantitative model that exposure of spring water with physiological characteristics to a static magnetic field for a brief period (1 hour) results in physical changes that are maintained for several hours before they dissipate. The time of the dissipation was related systematically with the volume of the water initially exposed to the magnetic field. In three separate trials (over separate days) for each volume of water removed from a 1600 G magnetic field after one hour of exposure, the time required for the doubling of diffusion velocities to occur for aliquots removed from 25 cc, 50 cc, and 100 cc of spring water increased systematically. Approximately 5.9, 7.4 and 8.6 hours after the field removal the samples from the 25, 50, and 100 cc volumes, respectively, displayed comparable magnitudes of increased diffusion of the solute. We are assuming that the comparable amplitude of delayed change in diffusion velocities was related to the magnetic field intensity (1600 G) to which all volumes was exposed. The doubling is consistent with the predicted values extrapolated from Fahidy (1992) that a 1.6 x 10-1 T magnetic field should decrease the viscosity by 95%, and this would be reflected by increased diffusion of solute.
The 50 cc volumes that were exposed to earth intensity magnetic fields did not show this change in diffusion. In addition, the water that had been exposed to two intensities of 7 Hz complex magnetic fields that have affected planarian activity (Gang and Persinger, 2011) also did not show any significant alterations in diffusion rates. In fact, the means for the three conditions exposed to the coil did not differ significantly from the earth-field reference measures for the 1600 G study.
The protracted nature of the increased diffusion velocity, relative to baseline and control samples, would be expected if energy had been stored in the water within a boundary condition, and then released. The effect was not transient, but was sustained for hours for each volume. We would not expect that any physicochemical change associated with the increased diffusion velocity to be indefinite. There should be a return to control levels after the energy had been dissipated. Measurements were not continued until dissipation completion time; this is of interest for continuing studies. However, Oshitani et al (1999) showed that the “memory effect” from the exposure of 10 cc of water to 0.4 T (4,000 G), which required about 20 min for a maximum effect, began to decay after 3 days and had disappeared by 5 days.
Based upon simple predictions from the product of the numbers of water molecules per mole (6.023 x 1023), free protons in solution (4 x 10-8 M), and the life time of a hydronium atom (~10-12 s) according to DeCoursey (2003), a first order homogeneous release of the “memory effect” from the exposure to the magnetic field would require at least 6,000 seconds to manifest. The value in our study was about 4 times longer, although this could be accommodated by variability in duration of hydronium ions and the actual concentration (rather than an estimate). The quantitative differences in change in the diffusion velocity did not double in time with volumes from 25 cc to 50 cc to 100 cc. Instead, there was a constant interval of about 8,000 sec (about 2.2 hr).
The alternating 7 Hz magnetic field treated water showed very different results than its static field treated counterparts. The stability in solute diffusion speed over the time measured suggests that either the magnitude of the intensity, the static property of the 1600 G field, or perhaps the duration (6 min vs 60 min) created the conditions for this effect. After a sufficient duration of exposure, which was longer than Oshitani et al’s (1999) 20 min, the stored energy was maintained until it was dissipated. We have suggested that a process involved with the life time (10-12 s) of the hydronium atom is involved.
There are three considerations based upon recommendations from a referee of the manuscript that should be addressed. First, although there were no conspicuous sudden maintained “relaxations” in the diffusion velocities for the samples exposed to the weaker (0.14 µT; 0.4 µT) 7 Hz time-varying fields compared to the exposures to the stronger (0.16 T) static field, there may have been an enhancement of the intrinsic power of the oscillation of the ~75 min period from only 6 min (vs 60 min for the static field) of exposure. When much weaker intensities of the appropriate time-varying fields affect the temporal distributions of power in an oscillating system rather than the total absorption or release of energy the insertion of information within the system by the pattern of the field becomes an important variable to consider.
Second, the possibility that the effects we observed are restricted to the narrow band of ambient temperatures requires careful assessment. There are phenomena, such as the biogenic liquid crystal state of the plasma membrane, that display specific structural properties (selective permeability) only within a narrow range of temperature (~37˚ C), pH and relative proportion of free water. The ambient temperature in our study was within a narrow band of ~ 25˚ C. Third, electrolytes within the spring water employed as the “general solvent” were selected for their relevance to physiological systems. The contribution of these ions to the specific latencies for the shifts in diffusion velocity of the solute should also be considered.
Bioinformation in temporally patterned fields has been shown to be imprintable and maintained in water samples (Pan et al., 2003). For very strong pulsed and alternating magnetic fields Oshitani et al (1999) found that the “memory” effect remained for at least 5 days and was present long after the “memory” from the static magnetic field had dissipated. If “intrinsic oscillations” (Rycroft, 2000) are significant contributors to the “memory” of water, we suggest that the microHz interval revealed by our spectral analyses (Figure 5) may be avenues for future investigation. That the larger (50 and 100 cc) water volumes treated by the static magnetic field showed significant diminish ment of power of the 75 minute oscillation indicates that a non-linear relationship may exist for the optimal volume of water treated by the applied magnetic field.
Acknowledgements
Thanks to Dr. Rob Lafrenie for his comments and inspiration.
References
Bett KE, Cappi JB (1965). Effect of pressure on the viscosity of water. Nature 207: 620-621.
Cook LL, Persinger MA, Koren SA (2000). Differential effects of low frequency, low intensity (<6 mG) nocturnal magnetic fields upon infiltration of mononuclear cells and numbers of mast cells in Lewis rat brains. Tox. Lett. 118(1-2): 9-19.
DeCoursey TE (2003). Voltage-gated proton channels and other proton transfer pathways. Physiol. Rev. 83(2): 475-579.
DeMeo J (2011). Water as a resonant mechanism for unusual external environmental factors. WATER 3: 1-47.
Del Giudice E, Spinetti PR, Tedeschi A (2010). Water dynamics at the root of metamorphosis in living organisms. WATER 2: 566-586.
Fahidy TZ (1999). The Effect of Magnetic Fields on Electrochemical Processes, In: 5, Modern Aspects of Electrochemistry, No. 32, B.E. Conway, J.O.M. Bockris and R.E. White Eds., Kluwer/Plenum, New York.
Gang N, Persinger MA (2011). Planarian activity differences when maintained in water pre-treated with magnetic fields: a nonlinear effect. Electromag. Biol. Med. 30: 198-204.
Oshitani J, Uehara R, Higashitani K (1999). Magnetic effects on electrolyte solutions in pulse and alternating fields. J. Col. Interface Sci. 209: 374-379.
Pan J, Lorenzen LH, Carrillo F, Wu H, Zhou M, Wang ZY (2004). Clustered water and bio-signal networks. Cybernetics and Intelligent Systems, 2004 IEEE Conference on, 2: 902-907.
Pan J, Zhu KN, Zhou M, Wang ZY (2003). Low resonant frequency storage and transfer in structured water cluster. Systems, Man and Cybernetics 5: 5034-5039.
Pollack GH, Figueora X, Zhao Q (2009). Molecules, water, and radiant energy: new clues for the origin of life. Int. J. Mol. Sci. 10: 1419-1429.
Preparata G (1995) QED Coherence in Matter. World Scientific, New York.
Rycroft MJ, Israelsson S, Price C (2000). The global atmospheric electric circuit, solar activity and climate change. J. Atmosph. Solar-Terres. Phys. 62: 1563-1576.
Smith CW (2004). Quanta and coherence effects in water and living systems. J. Alter. Complem. Med. 10(1): 69-78.
Walker JS (2004). Physics 2nd Ed. Person Education Inc., New Jersey. pp. 732.
Zheng JM, Chin WC, Khijniak E, Khijniak E, Pollack GH (2006). Surfaces and interfacial water: evidence that hydrophilic surfaces have long-range impact. Advances in Colloid and Interface Science 127: 19-27.
Discussion with Reviewers
Anonymous Reviewer: The submitted article is quite interesting. It provides a convincing evidence that the application of an external static magnetic field modifies the internal space of the liquid water in such a way that externally supplied molecules (ink) move clearly in a nondiffusive way. This evidence of a nondiffusive motion of molecules suggests that long-range fields are filling the intermolecular space and moreover these fields are able to assume the energy of the applied magnetic field and spread it in the intermolecular volume. The observed difference between the effects of the static and time dependent magnetic fields is intriguing, indeed. It looks like if the time dependent field would transfer its energy to the inner structures of the coherence domains, giving rise to long lived excited states of them, whereas the energy supplied by the static fields could be dissipated outwards in a faster way. Could be this a possible explanation?
Gang, St-Pierre & Persinger: It does appear as if water treated by the static magnetic field releases absorbed energy faster than what is observed in water treated by the time-dependent field. It is likely that this difference is not due to a changed capacity of the water to absorb applied energies, but rather due to the differences in application. This explanation would imply coherence between Schumann resonance and the naturally present resonance within spring water.
Reviewer: My second question is on the possible dependence of the observed effects on temperature. Do you expect a monotonous dependence of the change of diffusion velocities on T or it is more likely a dependence peaked in a particular range of T?
Gang, St-Pierre & Persinger: If the magnetic fields are influencing the special compartments of water then we would expect a narrow band of effect, much like the optimal temperature, pH, and relative water composition that generates the smectic meosphase which is characteristic of the selectively-permeable plasma cell membrane. However this is an experimental question.
Reviewer: My third question is whether the presence of solutes, electrolytes in particular, affects the outcome of the experiments in a significant way?
Gang, St-Pierre & Persinger: Whether the diffusion rate was influenced by the presence of solutes was not thoroughly explored. Spring water was employed for this study to allow for an investigation with a biologically relevant solution. A systematic examination of the effects biologically typical solutes may have upon the diffusion behavior of magnetically treated water, either individually or in concert, and in what concentrations, would have widespread implications in the fields of biophysics and electrophysiology.
