Energizing Water through Dynamic Flow
Johansson Ba,*, Trousdell Ib, Capjon Jc
a Akloma Bioscience AB, Medeon Science Park, 212 05 Malmö, Sweden
b Foundation for Water, Sussex, UK
c University of South-Eastern Norway, 31184 Borre, Norway
* Corresponding author: Email: benny@akloma.com
Keywords: Flowform, water ordering, reduction in IR emission, fractal scaling, long-range correlation, self-regulation, quantum dynamics
Published: January 28, 2021
Abstract
This study investigates the energy state in dynamic active flow obtained from four different flow-surface designs (i.e., Flowforms or FFs). The study was performed on two ceramic single-vessel units (i.e., the Manawa vase and Matatiki bowl), the three-vessel Glonn vertical stack, and the twelve-vessel Greenhouse vertical stack. The original water was a spring water obtained from Maglehem, Sweden. The results show that the Manawa vase and Greenhouse stack transform less organized low-grade thermal energy obtained from the environment into high-grade energy by means of the induced formation of energizing double-vortex figure-eight streaming flow in water through running water over a specific flow surface technology. The high and low-density liquid fluctuations of water from the Matatiki bowl and Glonn vertical stack vessels are proposed to shift toward a dominance of the high-density liquid, less than the 80% of ordinary water at room temperature and aligned with the tentative formation of a previously unidentified density state of liquid water. The thermal infrared (IR) emissions from the water surface as well as reduced redox potential and increased pH identified physically distinct concentric and condensed temperature gradient zones with long-term consistency, aligned as a low-entropy state of ordered coherence that implies a considerably decreased intrinsic mobile water state in water from all four FFs. A strong fractal power-law relationship revealed that fractal scaling geometry is part of coherent water ordering and that thermal IR flickering relates to a long-range correlation between water molecules, considered a manifestation of the underlying quantum dynamics in two of the four tested FFs, the Manawa vase and Greenhouse stack.
Background
Flowform (FF) water treatment technology is based on fixed, rigid flow surfaces designed to generate a rhythmic figure-eight oscillating flow of water with complex internal dynamic movements. FF technology was invented by John Wilkes in 1970 as a result of his mathematical and phenomenological research into form and flow in nature, and in particular into the phenomena of rhythmically oscillating streaming vortices, discovered by the physicist Theodore von Kármán in 1911 and subsequently named Von Kármán Vortex Streets (Virbelstrasse). This phenomenon, occurring when forces of inflow and resistance are balanced, was developed by John Wilkes A.R.C.A (1930-2011) into a flow surface Flowform® technology which generates a rhythmically steady, streaming figure-eight, complex dynamic flow powered only by the pull of gradient gravity. His purpose was to regenerate stagnant water by applying dynamic flow using a gravity-driven natural technology. Wilkes has previously described the invention and development of this dynamic biomimicry flow technology (Wilkes, 2003).
The Foundation for Water (FFW) (Web ref. 1) has continued Wilkes’ research and development achievements. Extensive experimental research projects have been summarized (Schwuchow et al., 2010) as part of this ongoing effort. FFW claims that flow-surface design technology can energize water in such a way that it can revitalize growth and improve health in organic nature. Other research has shown that low density coherent mineral water has such health-giving effects with impact on human health (Johansson, 2008, 2017; Johansson and Sukhotskya, 2016). FFW’s claim based on earlier mostly qualitative research is supported by cited research comparing FF-treated water with untreated water in terms of: (i) crystallization patterns of copper chloride dissolutions, (ii) capillary dynamolysis (“rising picture” method), (iii) round-filter chromatography (chroma method), (iv) drop-picture patterns, and (v) plant growth experiments (Loyter, 2010; Schwuchow et al., 2010). The first four methods convincingly reveal structured patterns in the treated water and the fifth method, growth experiments, demonstrates significant root length increase and plant morphology changes.
Since these methods are not generally accepted by mainstream natural science without support from quantified methodology, FFW has organized the present project. Its overall objectives are: (a) to find a method whereby the hypothesized energy increase in figure-eight rhythmic dynamic water treatment can be measured and interpreted in a consistent way and, if this can be achieved, (b) to correlate quantified scientific measurements with growth experiments. The present study was conducted to achieve objective (a). Objective (b) will be addressed in a follow-up study.
One important benefit of the capacity to measure different energy changes quantitatively is that this could lead to the more accurately targeted design of specific water rhythms and flow patterns in flow design technologies, and to the use of different design geometries and materials for effective energy increase and its potentially positive targeted effects in the future. Earlier research has explored figure-eight rhythms and sound frequencies (Thomas, 1983; Kristiansen et al., 1993; Wilkes, 2003; Schwuchow et al., 2010) and future work may be able to align specific frequencies and rhythms with measurable quantum coherence effects in treated water.

Figure 1. Left to right: Manawa, Matatiki, Greenhouse, Glonn design and sketch showing generic double-vortex oscillating figure-eight streaming flow path of water through all designs.
Material and Methods
Spring Water
Fresh spring water was obtained daily for each test and recirculated through FFs for two hours before taking 100-mL samples of water for temperature, chemical, and thermal infrared imaging (TIRI) analyses. Control water (fresh spring water) was equally conditioned at room temperature disconnected from FFs for two hours. Separately, a control test on fresh spring water was circulated through pumps only.
According to the Swedish food regulation, LIVSFS 2003:45 spring water is denoted as groundwater, able to be used as a drinking water in its natural state. It is bottled and packed at the water source (Maglehem) which is located in the east center of the district of Skane, Sweden. The quality of ground and drinking water in the area is very good and needs no purification or chlorination when used as a drinking water. Water quality is analyzed regularly and therefore we are assured that the source water quality remains the same across time.
Since the origin of natural spring water is deprived of dissolved air gases and constitutes a low redox-potential (~ 200 mV) (Web ref. 3), it denotes an accurate study water with high long-term chemical stability towards the impact of air gases (Web ref. 3).
Flowform Technology
The four Flowform (FF) designs are described in detail elsewhere (Schwuchow, 2010), and their appearance is as shown in Figure 1. The water outflow flow rate was as follows: Manawa vase, 5 liters per minute (lpm); Matatiki bowl, 5.5 lpm; Greenhouse vertical stack 2.5 lpm; and Glonn vertical stack, 14 lpm.
Submersible Pumps
Electrically powered submersible impeller pumps were used. The two ceramic units were each supplied with a SUNSUN HJ 731 pump with a magnetic rotational rod axle driving wing impellers. The Greenhouse stack was supplied with a Kockney KKYFP2400 pump and the Glonn stack with an Elpump CT 3274 pump. All pumps were placed in the water reservoir with approximately 15 cm of water covering the upper part of the pump to allow a stable recirculation of water through the pump, up through a flexible plastic pipe secured over each pump’s water flow exit to transport water to the higher point of entry in each FF vessel. From there, gravity carried it over the surfaces designed to enable a figure-eight flow path after which the water fell into the reservoir to be recirculated repeatedly.
Redox Potential, pH, and Conductivity
The control water samples from each pump were taken in sequence, two hours be-tween sampling, and conditioned for 30 min at room temperature before starting the analyses. The redox potential (ORP), pH, and conductivity were measured using an Inolab 740 multifunctional meter (WTW International, Stockholm, Sweden) as in our previous study of distilled water (Johansson, 2012). The ORP was measured using a SenTix® ORP electrode (WTW International, Stockholm, Sweden). The pH was measured using a high-stability Schott A77803K pH electrode (Schott AG, Mainz, Germany). The conductivity was measured using a TetraCon® 325 standard cell (Fisher Scientific, Gothenburg, Sweden). All three electrodes were located 2 cm below the surface of the bulk water sample. The ORP, pH, and conductivity electrodes were calibrated every day. The variation in the electrochemical stability of the ORP electrode was ± 5 mV. The ORP of the control or FF water (25 ml) stored in a 30-ml plastic or glass beaker (Fisher Scientific) was measured every 60 s for 120 min. The pH was followed in 25 ml of water for 90 min. until stability was reached. The conductivity was also followed in 25 mL of water for 60 min. Data were collected using Multilab® pilot software. The ORP, pH, and conductivity were measured as the mean ± SD of triplicates of each of three water samples.
Thermal Infrared Imaging (TIRI)
Thermal infrared image (TIRI) frames (1 cm2) were acquired using a RAZ-IR Thermal camera system 8–14 µm LWIR (collecting emitted light (photons) from the surface of water samples), thermal sensitivity ≤100 mK at 30°C, thermal resolution 160 × 120 pixels/frame, 25 µm; Sierra Pacific Innovations Corporation, Las Vegas, NV, USA) (Johansson, 2012). The equipment was set up in a very clean closed room used for analytical measurements. A sheet of aluminum foil was placed on a table beneath the camera to standardize the background emissivity. The camera was mounted and secured on a plastic stand and oriented vertically with the lens focused 7 cm (fixed position) from the top of two 45 × 10 × 10 mm vertical polystyrene optical cells (D-51588; Sarstedt, Aktien Gesellschaft & Company, Nümbrecht, Germany) containing 5.0 ml of control or experimental water. The cells were positioned and secured in an upright position 1.0 mm apart and conditioned at room temperature for 60 min. before measurement. Following “power on,” the camera automatically performed three non-uniformity calibrations (NUCs) after 5, 25, and 45 s. While turned on, the camera automatically performs NUCs at regular intervals. NUC allows automatic clean-up of the image noise, ensuring the normalization and sharpness of the live image. Six repeated image frames were acquired in sequence on a total of 20 water samples collected from each FF (measured at random intervals for two months) and saved for image analysis (i.e., temperature profiles of the pixel area and graphical representation of temperature data) using IR Analyzer software (Sierra Pacific Innovations Corporation). The temperature data were obtained from a defined pixel area of the water surface in each of the two cells; the image frames were transformed into numerical data by the IR Analyzer software and exported to an Excel spreadsheet for statistical evaluation.
Detrended Fluctuation Analysis
Detrended fluctuation analysis (DFA) (Peng, 1994; Goldberger, Web ref. 4) determines the fractal scaling of numerical temperature series data in the presence of possible trends without knowledge of their origin. The DFA algorithm permits the detection of intrinsic self-similarity embedded in non-stationary temperature series. The change in DFA exponent was calculated on mean temperature data from TIRI pixels obtained from a 1.0 cm2 area of the water surface.
The root mean square fluctuation of the integrated and detrended time series F(n) behaves as a power-law function of n:
(F(n) α nd) (1)
The integrated time series is divided into boxes of equal length, n. For each box of length n, a least square line is fitted to the data. The calculation is repeated over all time scales (box sizes). The DFA exponent, d, is defined as the slope of the regression line log n vs. log F(n). A DFA exponent of 0.5 ≤ d ≤ 1 indicates long-range power-law correlations, growing stronger toward 1. The change in the DFA exponent was calculated on mean temperature data from thermal IR emission pixels obtained from water.
Water Temperature
The temperature of control water and water obtained from the FFs (100 ml in 150 ml beakers of each water) directly at the end of the equilibration time was measured in duplicate (all together 30 sec.) using a Traceable® Ultraelectronic digital thermometer (VWR International AB, Stockholm, Sweden).
Time of the Study
Water samples from each of the four FFs were subjected to a total of 20 measurements, at random intervals from 13 June to 8 August 2018.
Statistics
Descriptive statistics were evaluated using SPSS statistical software. Data is presented as means ± standard deviations and a probability level of p < 0.05 is considered significant.
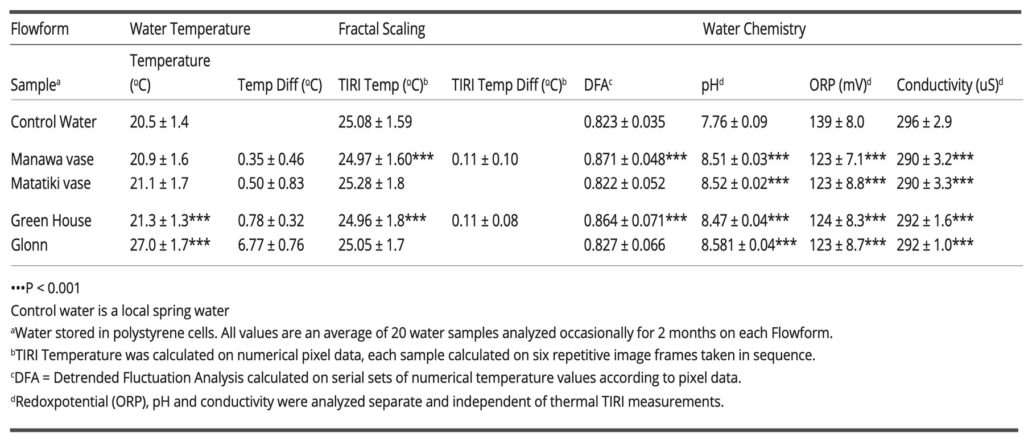
Table 1: Thermal infrared (IR) emossion imaging, fractal scaling and water chemistry in spring water circulating in flowforms for two hours.
Results
The mean results for the water temperature, fractal scaling properties (DFA exponent), and water chemistry (i.e., pH, redox potential, and conductivity) are shown in Table 1.
Water Temperature
The mean ± SD water temperature of control water was 20.5 ± 1.4°C. The temperature of the water from the two ceramic FFs had non-significantly increased to 20.9 ± 1.6°C (Manawa vase) and 21.1 ± 1.7°C (Matatiki vase). The serial multi-vessel FFs (i.e., the Greenhouse and Glonn stacks) made the water flow more complex, resulting in a significant increase in water temperature. The Greenhouse stack produced a minor increase in water temperature to 21.3 ± 1.3°C (p < 0.001), whereas the thermal influence of the Glonn stack produced a major increase of 6.8°C to 27.0 ± 1.7°C (p < 0.001). The possible mechanical heat influence from the interior of each of the running pumps as such and disconnected from the FFs showed no impact on water temperature (not shown). The high flow rate and turbulent flow of water with the steady formation of a high concentration of air bubbles within the flowing water may have contributed to the immediate and elevated water temperature obtained by the Glonn device. (Qiu et al., 2017). The minor increase in water temperature from the Greenhouse stack may be caused by the slowly flowing water, being distributed with the environmental heat energy dissipated across a large FF surface area.
Fractal Scaling and TIRI Temperature
The thermal IR emissions and water surface temperature in the FF water sample (from the Manawa vase) lower than the control water are illustrated in Figure 2. From the thermal IR control image (A), the structural ordering of the control water is illustrated by the red color zone (the temperature decreases according to the following color gradient: blue, blue/red, and red) along and close to the wall of the polystyrene cells, following a subsiding circular low-density temperature gradient. The IR emissions from the more distant regions in the center radiate normally. The IR radiation from the FF water (B) close to the interfacial zone expands toward the center and covers the entire water surface, following a lower color-density gradient toward the center. The structurally ordered and symmetrical layer is large and covers the entire water surface.
The results of DFA analysis (Table 1) reveal a clear power-law relationship in the thermal IR emissions from water obtained from the Manawa vase and Greenhouse stack. The DFA exponent increased significantly (p < 0.001) from 0.823 ± 0.035 (control) to 0.871 ± 0.048 in water from the Manawa vase; a similar irregular trend was observed in water from the Greenhouse stack, in which the DFA exponent increased to 0.864 ± 0.071 (p < 0.001). No change in DFA exponent was observed in water from the Matatiki and Glonn vessels. The change in DFA exponent indicates that the flickering of thermal IR emissions is characterized by highly persistent long-distance attraction due to non-thermal interaction between the molecules of water. The interaction of water molecules with the radiative IR electromagnetic field makes all molecules oscillate in unison, in tune with many self-trapped photons and a sizeable electromagnetic field, giving rise to a common phase within extended mesoscopic space regions, which is named coherent domains (CDs) (Del Giudice et al., 2009; Marchettini et al., 2010). In water CDs, the thermal fluctuation is aligned with and unifies the magnetic field oscillations of freely moving electrons, leading to long-range oscillation and structural stabilization among the coherent water clusters (Johansson, 2012). Thus, the existence of CDs implies the presence of ordering magnetic fields in ordered water.
The characteristics of the structural ordering of water molecules illustrated by the change in DFA exponent are correlated with the simultaneous decrease in water surface temperature. The IR emissions decrease and shift toward greater wavelengths (i.e., red shift). The water cools, with the ordered molecular structure of water from the Manawa vase generating a decrease in mean surface temperature of 0.11 ± 0.10°C (p < 0.001), comparable to that of the Greenhouse stack, i.e., 0.11 ± 0.08°C (p < 0.001). Since the difference in the IR emissions of the two FFs relative to those of the control experiment equals the adjusted decrease in surface temperature, the lower emissions substantiate the intrinsic ordering of water molecules that occurs due to the nonlocal characteristics of the FF surface flow path with impact on the flowing water molecules of these two FFs. Since it has been postulated that water´s hydrogen-bonding network can exist in two liquid forms of different density, namely high and low-density liquid water (Poole et al., 1992), it has been hypothesized that the observed high- and low-density amorphous ice forms are the glassy counterparts of the two liquid forms (Palmer et al., 2014). The existing understanding of molecular properties, structure and dynamics of liquid water is transferrable to the diffusive dynamics of high- and low- density transition in amorphous ice (Mishma and Stanley, 1998). Thus, with the decline in temperature the interfacial FF water is adjusted to form an amorphous non-crystalline-like state having local and distant configurative physical properties (Dubochet, 2016; Perakis et al., 2017). To the contrary, there was no change in the thermal IR temperature or DFA in water from the Matatiki vase and the Glonn vessel.
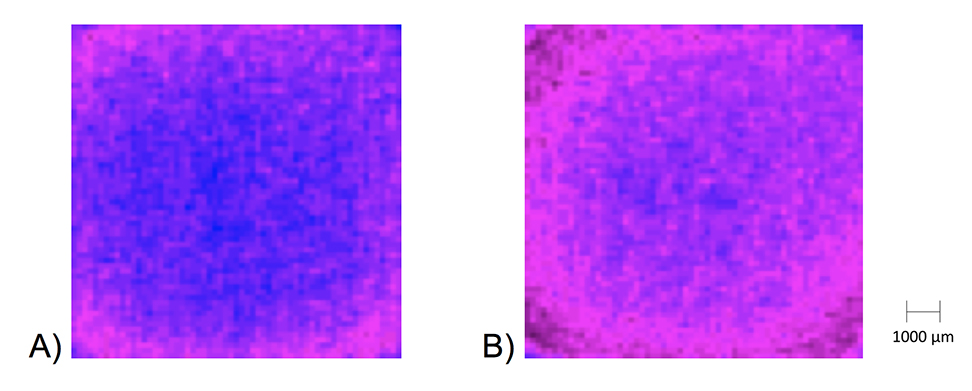
Figure 2. Thermal IR emissions at room temperature in control water (A) and FF water from the Manawa vase (B) stored in 5-mL polystyrene cells. The image of the FF water shows a higher state of structural organization of the liquid water. The mean temperature was on average 0.3°C lower in the experimental water. The temperature is decreasing according to the color gradient: blue, blue/red, and red.
Water Chemistry (pH, ORP and Conductivity)
The significant changes (p < 0.001) in pH, ORP, and conductivity in water from all four FFs (Table 1) are aligned with the state of water CDs, where the importance of long-range ordering with exceptional stability and feedback dynamics reflects the self-organizing ability with extended coherence of the inherent oscillations produced by the system itself (Froehlish, 1969; Del Giudice et al., 1985). The pH of the control water was 7.76 ± 0.09. A significant rise in the pH of the water was observed in all FFs (p < 0.001), resulting in a pH of 8.51 ± 0.03 (Manawa vase), 8.52 ± 0.02 (Matatiki vase), 8.47 ± 0.04 (Greenhouse stack), and 8.58 ± 0.04 (Glonn stack). In addition, the pH was significantly higher (p < 0.001) in the Glonn stack water than in water from the other three FFs.
Since tap water has an ORP between 220-380 mV, ordinary ground water around 250 mV, degassed pure water 200 mV and deep well water 0 mV (Web ref 3), the ORP of control water (Table 1), was found to be low (139 mV), which denotes a highly reductive spring water absent of dissolved gases. According to the theory of Nernst equation, the simultaneous increase in pH should be accompanied by a further decrease in ORP, which favors a more anaerobic condition (Web ref 3).
The shift toward a decrease in ORP accompanied by the rise in the pH of the ordered FF water indicates the self-regulative dynamics of circulating water aligned with long-range oscillations and lowered intrinsic entropy. This gives rise to structural ordering and allometric scaling behavior, all of which are characteristic of dissipative structures (Turning, 1952; Del Giudice and Tedeschi, 2009).
Accordingly, the significant change (p < 0.001) and decrease in ORP substantiates the existence of stabilized reductive water CDs that enable a reservoir of quasi-free electrons (Voeikov and Del Giudice, 2009), with the ORP being 139 ± 8.0 mV in the control water, with lower values in water from all the FFs: 123 ± 7.1 mV (Manawa vase), 123 ± 8.8 mV (Matatiki bowl), 124 ± 8.3 mV (Greenhouse stack), and 123 ± 5.7 mV (Glonn stack).
As the coherent ordering of water increases, the descending temperature will result in the dissolution of less mineral salts and a tendency to exclude minor particles, so the electric conductivity (EC) will subside (Israelachivli, 1992). Besides, since hydrogen ions concentrate at the boundary between the negative surface of CDs and the bulk volume of water, a small decrease in EC follows. The EC decreased equally and significantly (p < 0.001) from baseline (296 ± 2.9 µS) in water from all four FFs, varying at most from 290 ± 3.2 µS (Manawa vase) to 292 ± 1.6 µS (Greenhouse stack).
Discussion
In this study, the impervious designed flow-path surfaces of FFs were found to contribute to the natural low-entropy vortical flow dynamics of water. Vortical flow refers to the negative electrical charge of the high-grade energy of water from CDs moving in a loop enabled by the flow-path surface shape of FFs and producing circulating magnetic fields (Del Giudice et al., 2009; Marchettini et al., 2010). The theory of dissipative systems’ ability to self-regulate (Prigogine and Nicolis, 1977) implies that the exchange of energy and entropy with the environment relies on the fact that the absorption of external high-entropy thermal energy (i.e., rise in water temperature) by the water’s vortical path gave rise to low-entropy high-grade energy, displacing the equilibrium toward a dominance of water CDs. Likewise, the CDs of FF water were characterized by a distinctive configurative coherent aqueous state with a fractal scaling low-entropy relationship to radiative TIRI temperature fluctuations that maintained a self-organized structural adaptation irrespective of the water temperature (Johansson, 2012).
Consequently, the impact of an imposed disordering of water structure, according to classical theory due to the rise in temperature of flowing water, is anticipated to have local effects that extend no more than nanometers between molecular structures (Israelachivli, 1992). The existence of water CDs implies the presence of the non-local ordering of magnetic fields in ordered water. Since the ordered water is in a state of quantum coherence, it cannot decay thermally; instead, its lifespan extends for up to days or weeks and longer (Elia and Napoli, 2004). The intensity of thermal IR emissions from water is a function of temperature and structure (Zeng et al., 2006). Because of the structural stability of water CDs, the difference in emissivity is correlated with the considerably lower thermal IR emissions than those of the control water. The sustained and condensed temperature gradients with consistently lower temperatures that last for days are proof of the remarkable stability of excited states in ordered water. This agrees with the consistently increased pH of succussed water (Elia and Napoli, 2004). Similarly, the extreme stability of the water CDs confirms the presence of a coherent low-density water state that omits air gases dissolved in the highly ordered FF water.
When high-grade energy from the quantum field was captured by incident thermal photons, these photons were self-trapped and became coherent photons in an excited state, oscillating in phase with the quantum electromagnetic field (Del Giudice et al., 2005). At this point, i.e., a Lamb-like shift, a critical number of coherent water molecules were adjusted together and became enclosed within the CDs, where a phase transition occurred (Del Giudice, 2005). The coherent oscillations of the molecules in the water CDs no longer required any external supply of energy. These molecules had become stabilized and self-organized on all scale levels, which, in the coherent state of FF water from the Manawa vase and Greenhouse stack, were identical to a strong power-law relationship in the fractal scaling boundary of thermal IR emission flickering, characterized by high persistence and the existence of water CDs that enable a reservoir of quasi-free electrons (Del Giudice et al., 2009; Johansson, 2012). This observation is in accordance with the fact that liquid water can alternate between the two density states (Perakis et al., 2017). At room temperature there are adjustable fluctuations between a dominant 80% of the local high-density molecular clusters of water and the low-density liquid.
The water CDs from the two high-grade energy-producing FFs were activated to collect low-grade energy of high entropy from their environment and transform it by exciting coherent vortices of almost free electrons into high-grade energy of low entropy that can release this energy into useful work without thermal losses (Brizhik et al., 2009). In contrast, the activation of water by the Matatiki bowl and Glonn stack flow-path surfaces lacks a nonlocal coherent water state due to the finding of unaffected fractal scaling properties. On the other hand, the specific impact of high-grade energy on water chemistry illustrates a differentiation in the high-grade energy state between the investigated FFs. The impact on the water from each FF is tentatively and specifically affected by its novel flow-path surface. The non-activating FFs adjust the fluctuations between local structures of high and low-density liquid towards a high-density balance, proposed less than 80 % (compared to a dominance of the high-density liquid around 80 % in ordinary water at room temperature), aligned with a plausible formation of an unknown density state of liquid water. The existence of several water density states was explicitly demonstrated as fluctuating water density gradients in the so-called floating water bridge (Fuchs, Web ref. 5). The intriguing observation of an unknown density state in FF water will be further explored in future studies.
The accumulation of quasi-free electrons accompanied by negative reductive charges may be attributed to single CDs or multiple nonlocal CD clusters. There may even be groups of rotating CDs moving in a loop, producing local circulating interacting magnetic fields. Such circulating charges could appear over a wide range of scales, from nanometers or less to several meters. The rotational speed of the reductive change depends on the resistance of the environment in which the charge moves. In special cases, this resistance approaches zero, which equals a superconducting system largely resulting from a quantum state (Czerlinsky, 2013). Our findings may indicate that the lower TIRI temperature of water from the Manawa vase and Greenhouse stack, as opposed to the non-activating FFs, tunes a transition water CD state toward a greater dominance of local temperature density fluctuations characteristic of low-density liquid water (Perakis, et al., 2017).
These CDs are receptors of weak nonlocal EMF signals (Del Giudice et al., 2005). Water molecules become structurally clustered and attract not only adjacent water molecules but also other guest molecules able to resonate at the same frequency (Brizhik et al., 2009). With a further increase in density, the water CDs become net exporters of energy because the self-stabilized coherent state has lower energy than the ionization threshold of water in an ordinary state (Del Giudice et al., 2005). Such coherent water CDs contain millions of nonlocal clustered water molecules in a low-entropy state and have a non-vanishing probability of containing an infinite number of quasi-free electrons that can be readily donated to electron-acceptor systems. The quasi-free electrons, considered the most significant property of quantum coherent systems, form frictionless vortices with an extremely long lifespan (Del Giudice and Tedeschi, 2009) lasting from days to weeks depending on a self-regulated magnetic moment that aligns coherent intrinsic and external vortices that cannot degrade thermally.
In view of the novel observation of a self-stabilized coherent FF state of water from the Manawa vase and Greenhouse stack, the water CDs could act as donors of excited electrons or catalyze the excitation of electrons to a fairly low activation energy. Thus, sufficient electrons are disentangled to account for a sustained reduction in the ORP in water CDs, where the numerous leaking electrons expand the low-density water state and may be released through either modest excitation or the quantum tunnel effect (Del Giudice and Tedeschi, 2009). The release of electrons from the water CDs leaves behind hydroxyl ions, which reach the high-density fraction of water, supporting a rise in pH. A concomitant array of water CDs, whose extended coherence depends on the presence of non-aqueous guest molecules, causes the production of a magnetic vector potential from EMFs trapped in the water CDs (Del Giudice et al., 2005; Brizhik et al., 2009). Accompanied by a strong power-law relationship, the fractal scaling boundary of the thermal IR emission flickering in ordered water reflects an indicative high degree of self-similarity over multiple scales (Mandelbrot, 1983; West et al., 1997). Intriguingly, the surrounding nonlocal space gives rise to a magnetic vector potential whose rotor and hence magnetic field extends far into the environment (Del Giudice et al., 2010). Therefore, there exists a coupling between the vector potential produced by water CDs of activating FFs and the vector potential originating in the electrodynamics occurring in the adjacent or distant environment, like the electromagnetic radiation produced by sunspots, cosmic events, and atmospheric events (Del Giudice et al., 2010), i.e., corresponding to the Aharonov-Bohm effect (Peshkin and Tonomura, 1989).
The state of the underlying trend has a degree of autocorrelation characterized by high persistence or long-term memory. The strong persistence of the DFA exponent indicates that the water temperature fluctuations from small to larger temperature intervals are positively correlated in a power-law fashion. Thus, a tendency for a decrease in water thermal IR emissions is followed by another decrease in water IR emissions at a different location related to fractal scaling behavior. This implies that the long-range correlation should be considered an important factor in the trend prediction of water thermal IR emissions. Additionally, the DFA exponent of water is strongly related to the structural adaptation capability of the water body. Water with a high DFA exponent (i.e., approaching 1.0) can maintain the fluctuation tendency of thermal radiation even when the external temperature changes, decreasing the entropy of the system and giving rise to potential self-organization (Del Giudice and Tedeschi, 2009).
Conclusion
A highly organized and coherent low-density liquid water state forms in the dynamic water flow of the designed flow-path surfaces of the Manawa and Greenhouse stack FF vessels which is an observation aligning with the main study objective. The difference between low-density activating and non-activating FF designs causing different vortical paths of flowing water is aligned with the fact that liquid water can alternate between two density states. Despite variation in FF water temperature fluctuations during the study period, the repeated formation of nonlocal low-density liquid dominated the dynamics of the coherently flowing water. The results are conjectured to support the quantum electrodynamic nature of the vortical flow-path surfaces of the Manawa vase and Greenhouse stack. In addition, it is proposed that the formation of an unknown density state by non-activating flowing FF water (Matatiki bowl and Glonn vertical stack) shifts the high and low-density fluctuations toward a restricted dominance of high-density liquid.
Discussion with Reviewers
Reviewer: Why do the authors say that “magnetic field oscillations of freely moving electrons lead to long-range oscillation and structural stabilization among the coherent water clusters”? Where does the magnetic field exist?
Authors: According to the existence and formation of coherent domains (CDs) in water, (Del Giudice, et al., 2009 and Marchettini, et al., 2010), a collection of free electrons can produce cold vortices that have a quantifiable magnetic moment aligning them to ambient magnetic fields. Thus, the existence of CDs implies magnetic fields in ordered water.
Reviewer: TIRI temperature – if water temperature increases, why does the surface temperature decrease?
Authors: Directly after the pumps were turned off the “physical temperature” of water was measured on collected water with an electronic temperature meter which shows the temperature in real time. The TIRI temperature is taken off photons emitted from the water surface, measured from the top of two polystyrene optical cells, containing 5.0 ml of control or experimental water. The cells were conditioned for 60 min before measurement. The difference in TIRI temperature and/or DFA is a measurement of the fractal coherency of water, which has a long-term stability for many days or even extending to months. It represents a quantum coherent state of water.
Reviewer: Why are there a difference in these results between the 4 devices?
Authors: The main difference between the two low-density activating and non-activating FFs depends on the impact of an imposed disordering of water structure. According to the classical theory, the rise in temperature of flowing water is anticipated to have local effects that extend no more than nanometers between molecular structures (Matatiki bowl and Glonn stack). The existence of water CDs (Manawa vase and Greenhouse stack) implies the presence of the nonlocal ordering of magnetic fields in ordered water. Since the ordered water is in a state of quantum coherence, it cannot decay thermally; instead, its lifespan extends for up to days or weeks and longer. The result suggests that the two FFs, which gave high water fractal coherency, appeared to have much smoother double-vortex figure-eight streaming flow pattern with a harmonious rhythm. Thus, the dynamic water flow of different FF design geometries and materials could be a question for further research, not addressed in this research paper.
Reviewer: With the decline in temperature, the interfacial water is adjusted to form an amorphous non-crystalline-like state, having local and distant configurative physical properties – is it really so and is it related to the current experiment?
Authors: The existing understanding of molecular properties, structure and dynamics of liquid water is transferrable to the diffusive dynamics of high- and low-density transition in amorphous ice. Thus, the water´s hydrogen-bonding network that exist in two liquid density states (high and low-density liquid water) have been suggested to be the glassy counterparts of high- and low -density amorphous ice forms (Poole et al, 1992; Palmer et al, 2014 and Mishma and Stanley, 1998).
Reviewer: The significant difference between temperature of water after it was treated in the Glonn device and other devices and of control water is surprising. The authors suggest that elevated temperature may be due to “the high flow rate and turbulent flow of water with the steady formation of a high concentration of air bubbles.” However, a small but as it is claimed significant increase of temperature over the control was observed in water treated in the Greenhouse device with the lowest flow rate of water, while temperature of water treated by the two other devices where flow rate was twice as high as in the Greenhouse device but lower than in Glonn device did not differ from control water temperature. So, the authors’ explanation of this effect does not seem convincing.
Authors: The temperature in the Glonn device was much higher than the control and it was expected from previous studies, due to the extremely turbulent water through the FF creating kinetic energy. When it comes to the Greenhouse stack the height of the stacks is more than 2 m, which allows the slowly flowing water to be exposed and distributed over a large FF surface area, explaining the higher temperature.
Reviewer: It is unclear why there exists such a discrepancy between temperatures of water measured using the digital thermometer and TIRI both in absolute values and between different water “brands” why does control water temperature, measured using the digital thermometer, show 5 ºC lower than if it is measured using TIRI? One may expect that that TIRI measures surface temperature of water and as water is evaporating its surface temperature should be lower than bulk water temperature, but the measurements give opposite picture. Why is it so? Besides, temperature of water using the Glonn device measured by a digital thermometer is nearly 7 degrees higher than control water temperature, while TIRI does not show any big difference between temperatures of different specimens of water. On the other hand, there is no difference in temperature measured using digital thermometer in control and Manawa vase treated waters, while it is claimed that TIRI reveals though small but significance difference between these two specimens of water. It is also unclear why water treatment with two not evidently different devices (Manawa vase and Matatiki vase) produces waters with different properties according to TIRI and DFA measurements.
Authors: The questioned discrepancy between temperatures of water measured using a digital temperature meter “physical temperature” or TIRI (measuring temperature and fractal behavior of emitted water surface IR photons) was expected, because we are measuring two different states; the physical temperature is a 4D high density state, while TIRI illustrates the fractal ordering of the low-density state, i. e. the quantum state of water. This discrepancy depends on the fact that the digital measurement was made on a sampled volume of collected FF-water promptly after the two hours recirculation/equilibration time of water through the FFs. On the other hand, the TIRI temperature was measured from emitted surface IR photons of FF-water stored in two 5 ml polystyrene optical cells (5 ml of control or FF-water) after one-hour conditioning at room temperature. The TIRI temperature difference between control and experimental water is also illustrated in Fig 2. Due to formation of a low energy and low-density state of coherent water in the experimental water, follows a lower temperature and more organized (increase in DFA) water state. Moreover, the “physical temperature” is a 4D measurement, while the TIRI (temperature and DFA) reveals an extremely stable quantum state i.e., the thermometer and TIRI measures two different states of water.
Reviewer: As it can be seen from Table 1 after FF water treatment irrespective of the devices pH, ORP and conductivity of all specimens change significantly in comparison with control water. The authors interpret these changes in the frame of concepts basing on the existence of CDs in water. It may be so, but the purpose of the paper was to understand the specific effect of different flow-surface designs or FF water treatment on water properties. All the changes in “chemical” properties of water after its treatment may be related to the loss of CO2 from water that was agitated during its flow through FF devices and not due to a specific FF treatment that is based on “on fixed, rigid flow surfaces designed to generate a rhythmic figure-eight oscillating flow of water with complex internal dynamic movements” as it is written in the Introduction. To check this one may compare properties of FF-treated water with those of water after simple stirring or by other agitation procedure. I suspect that such trivial treatment of spring water should result in an increase of its pH, decrease of its ORP due to pH increase (Nernst equation) and small decrease in conductivity because of decrease in concentration of free ions in water. Indeed, all these changes may be related to changes in water dynamic structure, but do they prove that there is any specific effect of “a rhythmic figure-eight oscillating flow of water with complex internal dynamic movements” on these water properties in comparison to simple water agitation?
Authors: Since it is known that degassed pure water has an ORP of 200 mV (Web ref. 3) and that the ORP of control water in the present study was 139 mV (Table 1) and even lower in experimental samples (123-124 mV), the results clearly denote a highly reductive spring water absent of dissolved gases. A further recirculation of water through the FFs could tentatively add some dissolved oxygen in water, where increased oxidation and thereby ORP would follow. Similarly, environmental carbon dioxide could be dissolved and added in water, giving a decrease in pH. In fact, the results were opposed with a further decrease in ORP and increase in pH, indicating the absence of oxygen and other dissolved air gases. This observation may depend on the extreme stability of the coherent low-density state of water, that would omit air gases to be dissolved in the water. Further, according to the theory of Nernst equation, the simultaneous increase in pH would be accompanied by a further decrease in ORP, which favors more anaerobic conditions. Consequently, the impact of a clarifying experiment composed of simple water agitation would be of no value. Furthermore, highly organized water is extremely stable towards temperature changes (Johansson, 2012). Since the ordered water is colder, dependent on coherence, it cannot decay thermally. Instead, its lifespan can be extended even for months. (Del Giudice and Tedeschi, 2009; Elia and Napoli, 2004).
Acknowledgement
The authors are grateful to Software AG – Stiftung (SAGST), Darmstadt, Germany for funding the study. The funding had no role in any part of the study.
References
Brizhik L, Del Giudice E, Jörgensen SE, Marchettini N, Tiezzi E. The role of electromagnetic potentials in the evolutionary dynamics of ecosystems. Eco Model. 220, 1865-1869, 2009.
Czerlinsky G. On the new physical biology. Vortex Sci Technol. 1, 1, 2013.
Del Giudice E, De Ninno A, Fleischmann M, Mengoli G, Miliani M, Talpo G, Vitiello G. Coherent quantum electrodynamics in living matter. Electromagn Biol Med. 24, 199-219, 2005.
Del Giudice E, Doglia S, Milani M, Vitiello G. Electromagnetic field and spontaneous symmetry breaking in biological matter. Nucl Phys B251 (FS13), 375-400, 1985.
Del Giudice E, Spinetti PR, Tedeschi A. Water dynamics at the root of metamorphosis in living organisms. Water 2, 566-586, 2010.
Del Giudice E, Tedeschi A: Water and autocatalysis in living matter. Electromag Biol Med. 28, 46-52, 2009.
Del Giudice, Pulselli RM, Tiezzi E. Thermodynamics of irreversible processes and quantum field theory: an interplay for the understanding of ecosystem dynamics. Ecol Model. 220, 1874-1879, 2009.
Dubochet, J. A Reminiscence about Early Times of Vitreous Water in Electron Cryomicroscopy. Biophys J. 110, 756-757, 2016. Rewarded the Noble prize in chemistry 2017.
Elia V, Napoli E. New physio-chemical properties of extremely diluted aqueous solutions. J therm Anal Calorim 75, 815-836, 2004.
Froehlish H. Theoretical physics and biology. In: Proceedings of the first international conference on theoretical physics and biology. Marios M, ed. Versailes, Amsterdam, Holland, 1969.
Israelachivli J. Intermolecular and surface forces. San Diego, Academic Press, 1992.
Johansson B. Heart rate and heart rate variability response to the transpiration of vortex-water by Begonia Eliator plants to the air in an office during visual display terminal work. J Alter Compl Med. 14(8), 993-1003, 2008.
Johansson B, Sukhotskya S. Allometric scaling behavior – A quantum dissipative state implies a reduction in thermal infrared emission and fractal ordering in distilled coherent water. Water 3, 100-121, 2012.
Johansson B, Sukhotskya S. Drinking functional coherent mineral water accompanies a strengthening of the very low frequency impact on heart rate variability, and mono and multifractal heart rhythm dynamics in healthy humans. Function Food Health Dis. 6(6), 388-413, 2016.
Johansson B. Functional water – in promotion of health beneficial effects and prevention of disease. Int Med Rev. 2(12), 1-24, 2017.
Loyter O. The effect of Flowform treatment on cress germination and growth. In: Energizing Water, Flowform Technology and the Power of Nature. Schwuchow J, Wilkes J, Trousdell I, eds. Sophia Books, Forest Row, UK, 71-77, 2010.
Mandelbrot BB. The fractal geometry of nature. New York. W.H. Freeman and Company, 1982.
Marchettini N, Del Giudice E, Voeikov V, Tiezzi E: Water: A medium where dissipative structures are produced by coherent dynamics. J Theor Biol. 2010, 265: 511-516.
Mishima O, Stanley HE. The relationship between liquid, supercooled and glassy water. Nature 396, 329-335, 1998.
Palmer JC, Martelli F, Debenetti PG. Metastable liquid-liquid transition in a molecular model of water. Nature 510, 385-388, 2014.
Peng CK, Buldyrev SV, Havlin S, Simons M, Stanley HE, Goldberger AL. Mosaic organization of DNA nucleotides. Phys Rev E 49, 1685-1689, 1994.
Perakis F, Amann-Winkel K, Lehmkühler F, Sprung M, Mariedahl D, Sellberg JA, Pathak H, Späh A, Cavalca F, Schlesinger D, Ricci A, Jain A, Massani B, Aubree F, Benmire CJ, Loerting T, Grübel G, Pettersson LGM, Nilsson A. Diffusive dynamics during the high-to-low density transition in amorphous ice. PNAS, 114(31), 8193-8198, 2017.
Peshkin M, Tonomura A. The Aharonov-Bohm Effect. Springer-Verlag, Berlin, Germany, 1989.
Poole PH, Sciortino F, Essman U. Phase behaviour of metastabile water. Nature 360, 324-328, 1992.
Prigogine I, Nicolis G. Selforganisation in non-equilibrium systems, from dissipative structures to order through fluctuations. Wiley, New York, 90-160, 1977.
Qiu J, Zou Z, Wang S, Wang X, Wang L, Dong Y, Zhao H, Zang L, Hu J. Formation and stability of bulk nanobubbles generated by ethanol-water exchange. Chem Phys Chem 18(19), 1345-1350, 2017.
Schwuchow J, Wilkes J, Trousdell I. Energizing Water, Flowform Technology and the Power of Nature, Sophia Books, Forest Row, UK, 2010.
Turning M. The chemical basis of morphogenesis. 237, 37-72, 1952.
Voeikov VL, Del Giudice E. Water respiration-the basis of the living state. Water 1, 52-75, 2009.
Wilkes J. Flowforms: The Rhythmic Power of Water. Floris Books Edinburgh UK, 2003.
West GB, Brown JH, Enquist BJ. A general model for the origin of allometric scaling laws in biology. Science 276, 122-126, 1997.
Zheng J-M, Chin W-C, Khijniak E, Khijniak Jr E, Pollack GH. Surfaces and interfacial water. Evidence that hydrophilic surfaces have long-range impact. Adv Coll Interf Sci 127, 19-27, 2006.
Web References
1. Foundation for Water (FFW) www.foundationforwater.org
2. Von Kármán, T. Vortex shedding, the unsteady separation of fluidic flow. https://en.wikipedia.org/wiki/K%C3%A1rm%C3%A1n_vortex_street, June 2020
3. Chaplin M. Water redox processes. www.1.lsbu.ac.uk/water/water_structure_science.html, 2019.
4. Goldberger AL. Fractal dynamics in physiology. Alterations with disease and aging. PNAS 99, 2466-2472, 2002. Software for calculation of DFA was downloaded from www.physionet.org/physiotools/dfa
5. Fuchs E. www.ecfuchs.com
