SPECIAL EDITION
High Dilutions
Non-Monotonous Impedance Patterns of Diclofenac Centesimal Potentiated Solutions and Their Evolution
Lobyshev VI
Faculty of Physics, Lomonosov Moscow State University. 119991 Moscow, Russia
lobyshev@yandex.ru
Keywords: ultrahigh dilutions; water; diclofenac; permittivity; resistivity; active oxygen forms
• Received: November 8, 2021
• Revised: January 22, 2022
• Accepted: February 16, 2022
• Published: April 25, 2022
Abstract
The impedance of heavily diluted diclofenac centesimal potentiated solutions in the range of 20 Hz – 10 MHz was studied. Each dilution was accompanied by vigorous shaking. The whole set of samples consisted of 33 iteration steps. Two parallel sets were prepared. There was no permittivity increment in the samples, which indicates the absence of mesoparticles with high dipole moment. At the same time, the resistance of the samples presented a non-monotonic character, including ultra-high dilution samples, in which the concept of diclofenac concentration does not make sense. The pattern of both sets of samples turned out to be well correlated. The evolution of the resistivity patterns consisted of a decrease of the average value with a significant preservation of the shape of the pattern up to 30 days. This means that the result does not depend on the concentration of the solute, but on the sample preparation procedure. A hypothetical explanation of the observed effects consists in the appearance of reactive oxygen and nitrogen forms during mechanical perturbation of solution and the products of subsequent complex chemical reactions.
Introduction
Water is a polar liquid of high permittivity that makes it a good solvent for polar and ionic substances. These substances at not very high concentrations produce ideal aqueous solutions where solutes do not interact with each other, and solutions are homogeneous. The main concept for physico-chemical properties of diluted ideal solutions consists of a monotonic tendency to the properties of a solvent at high dilutions. In practice, solutions of 10-4 M concentration and lower are named as infinitely diluted solutions. Amphiphilic substances at certain concentrations in water, called the critical concentration of micelle formation (CMC), self-organize into colloidal structures – various types of micelles. These CMC points are registered as kinks on the plots of various physical characteristics (viscosity, conductivity, sound speed, light scattering, etc.) upon concentration of amphiphilic substances. The values of the CMC are in the range of 10-4-10-2 M. Structural inhomogeneities in binary systems, including water-alcohols or other non-electrolytes, have also been known for a long time. They are characterized by two maxima of the scattered light intensity caused by the appearance of inhomogeneities in the solution. In the case of water-alcohol, the main one is wide on the scale of concentration of the added component at the molar fraction of alcohol X= 0.2-0.5 and the other, narrower, at X= 0.01-0.05. The main maximum is caused by concentration fluctuations but the nature of the sharp maximum at a lower concentration is still not completely clear (Bulavin et al. 2016). It was found that the equilibrium in these solutions is established for a long time, up to several days after mixing the liquids. Mesoscale inhomogeneities can exist also in surfactant-free microemulsions (SFME) in ternary systems consisting of relatively short amphiphilic components (hydrotrope) and two nearly immiscible liquids. The unique mesoscope structuring in SFME offers various opportunities. For example: SFME are powerful solubilization media, providing anomalies in enzymatic activity and chemical reactivity when used as reaction media (Hahn et al. 2019; Krickl et al. 2018). All described inhomogeneities registered by various physical methods appear at concentrations higher than 10-5M.
From the second half of the 1970s on, a wide range of concentrations of biologically active substances on various functions of biological model systems were studied that demonstrated polymodal non-monotonous dependence of biological (biochemical) response on the scale of concentration (Perchikhin et al. 1977; Yamskova et al. 1977a, b; Burlakova et al. 1986; Burlakova, 1999; Molochkina et al. 1999). A typical example is a two-optimum curve of protein kinase C inhibition upon concentration of the antioxidant α-tocopherol (Palmina et al. 1999). The singularity of this dependence consists in the presence of a maximum at low (they are also called ultra-low) concentrations of the active substance in the region of 10-14 M and the “dead zone,” which usually lies in the region of 10-7–10-11 M. When antioxidant concentration increases to 10-4 M, the usually observed maximum of activity appears. Another possible feature of highly diluted solutions is that their significant effect can be manifested against the background of a greater endogenous concentration of the same substance in the studied models. For example, opioids modulate the immune activity of various cells at concentrations of
1018–10-14 M, although the same opioid peptides are present in cells at a much higher natural concentration of 10-10–10-12 M (Brown and Van Epps, 1985; Zaitsev et al.1991). Similar effects were found also with the combined action of pharmacological agents and homeopathic preparations in high dilution (Epstein, 2008, 2013).
The uniform non-monotonic polymodal response of various model systems on the concentration of an active reagent in the region of low and ultra-low concentrations makes us think about the common cause of these effects. A common component of all these experiments is water. It is often possible to find a statement that the observed complex effects are related to the structure of water, but without giving sufficient arguments. Earlier we showed that highly diluted solutions of amino acids without chromophore groups possess a sharp increase in luminescence and explained it by self-organizing of the excited state regions with a size of about 100 nm (Lobyshev et al. 1994, 1999; Lobyshev, 1999). Later the clustering-triggered emission of solutes without traditional chromophores were reviewed (Wang et al. 2020).
Technically, it is more convenient to obtain solutions of low concentrations of biologically active substances by diluting a more concentrated solution. In many cases, low concentrations are achieved by the same type of sequential dilution (by 10 or 100 times, or in another proportion) followed by active mechanical shaking after each dilution, leading to rapid turbulent mixing of the solution. This method of sample preparation corresponds to the technology of preparation of drugs adopted in homeopathy. The so-called potentiated samples with an ultra-high degree of “dilution” can reach and even exceed the Avogadro limit where the concept of concentration loses its meaning. In this case, it is appropriate to talk about the number of these iterations (dilutions) only and to call the dependence on the number N of iterations a pattern.
Using this technology, we studied the fluorescence intensity of decimal sodium chloride dilutions including N=23 iterations. The pattern for fluorescence intensity occurred to be non-monotonic with a sharp maximum at N=13 where water should be considered as a fresh one. It is obvious that the salt solution will play the role of a stress factor for freshwater unicellular organisms. For the first time, we have shown that the intensity of fluorescence in the region of its maximum has a high negative correlation with the spontaneous mobility of freshwater unicellular infusoria Spirostoma ambiguum (Lobyshev et al. 2005). The presence of non-monotonic dependences of various physico-chemical characteristics in the concentration range of 10-2–10-18 M, their connection with the appearance of nanoparticles, and the corresponding change in biological activity has been repeatedly confirmed (Ryzhkina et al. 2009, 2013, 2019, 2021). In our previous paper, we studied electric properties of centesimal diclofenac solutions prepared by 14 iterations (Lobyshev, 2019). In the present paper, we demonstrate the resistivity patterns of centesimal dilutions of diclofenac with the number of iterations up to N = 33.
Materials and Methods
Testing solutions were prepared using ultrapure MQ water with the specific resistance of 18.2 MΩ cm obtained by purifying distilled water in the Merck Millipore Simplicity System and diclofenac sodium salt (Sigma-Aldrich D6899). The structure of diclofenac is shown in Figure 1. Preparation of the samples was as follows. At first, a diclofenac solution with the concentration of 1 mg/ml or 3.14 *10−3 M was prepared. To avoid large particle contamination and unsolved aggregates, the solution was filtered through the 0.2 μm sterile Sartorius Minisart membrane. This solution was labeled C1 and used to produce samples of centesimal serial dilutions. An amount of 0.1 mL was taken from this sample and poured into a bottle containing 9.9 mL of MQ water. These samples were labeled C2, C3,…C33. Each dilution was accompanied by 20 seconds’ potentiation, meaning vigorous shaking by manually tapping half-filled capped vials on the table surface similar to the stop flow method. All the samples were prepared in 20 mL glass vials with polypropylene screw caps and chemically inert teflon septa (Infochroma AG). Two parallel sets of dilutions M(C2, C3,…C33) and #M(#C2, #C3,…#C33) were prepared and were stored in a closed cardboard box under room conditions.
Figure 1. The chemical structure of diclofenac.
Impedance characteristics of aqueous diclofenac solutions were measured in a cell with coaxial cylindrical titanium electrodes using Wayne Kerr 65120 BD1 precision impedance analyzer. The volume of the cell is 0.6 ml. The cell has a jacket to maintain the temperature accuracy no worse than 0.1°С using a water thermostat. Measurements were carried out at the temperature of 28°С. The measuring cell was filled three times by the sample under investigation to establish the stationary value. The ultimate error of the measured quantities was below 0.5%. A parallel equivalent scheme for the cell was used that allows the analysis of resistance and capacitance of the cell in the frequency range 20 Hz-10 MHz. To eliminate the effects related to polarization of the metallic electrodes, the main part of the experiments was conducted at the frequency 100 kHz. All other technical details can be seen at Lobyshev (2019). The first set of measurements was performed on the next day after preparation of the samples. Next, measurements were carried out at 7, 14 and 30 days after preparation of the samples.
Results and Discussion
Dispersion effects in a wide 20 Hz-10 MHz frequency range were not observed, except for the polarization of titanium electrodes at frequencies below 30 kHz. The dielectric constant with an accuracy of 0.2% at frequency 100 kHz remains constant, which indicates that there is no appearance of particles with a large dipole moment in the sets of dilution. Figure 2 illustrates the patterns for the resistance of two parallel sets of potentiated dilutions M and #M.
The plot does not contain sample C1 because its corresponding resistance naturally sharply differs from the subsequently diluted samples, and requires a change in the scale that does not allow analyzing data from high dilutions.
The experiment carried out 7 days after the preparation of samples is not given to simplify Figure 2. One can see that the procedure of vigorous shaking during each step of dilution results in non-monotonic changing of the sample resistance significantly exceeding the experimental error. This feature persists from N=11 up to N=33, where the concept of diclofenac concentration in solution has lost its meaning. The evolution of patterns occurs during the storage of the samples. Over time, the average resistance of the samples decreases, i.e. their conductivity increases, but the shape of the pattern remains. The patterns of two parallel sets are similar also. The results of linear correlation analysis are given in Table 1.
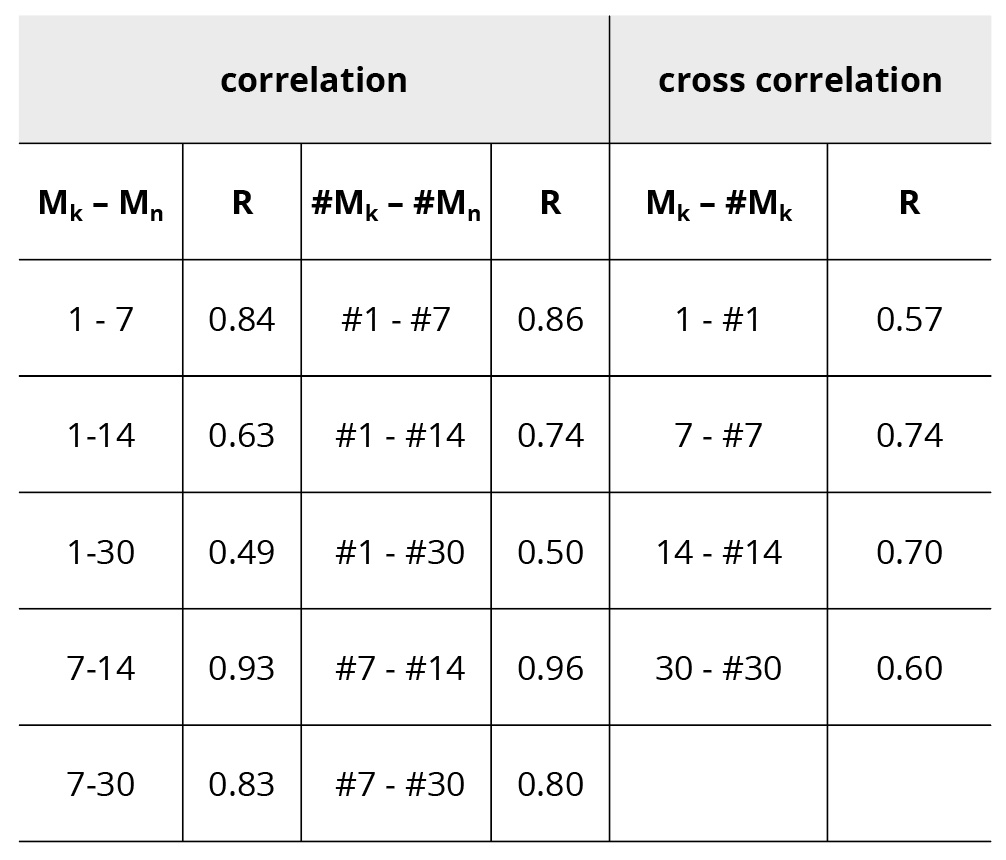
Table 1. Correlation coefficients R between patterns M of various days (k,n =1-7-14-30) after preparation and cross correlation coefficients R between patterns M and #M . Critical values for correlation coefficient are: Р0.05(30) = 0.35; Р0.01(30) = 0.45; Р0.001(30) = 0.55
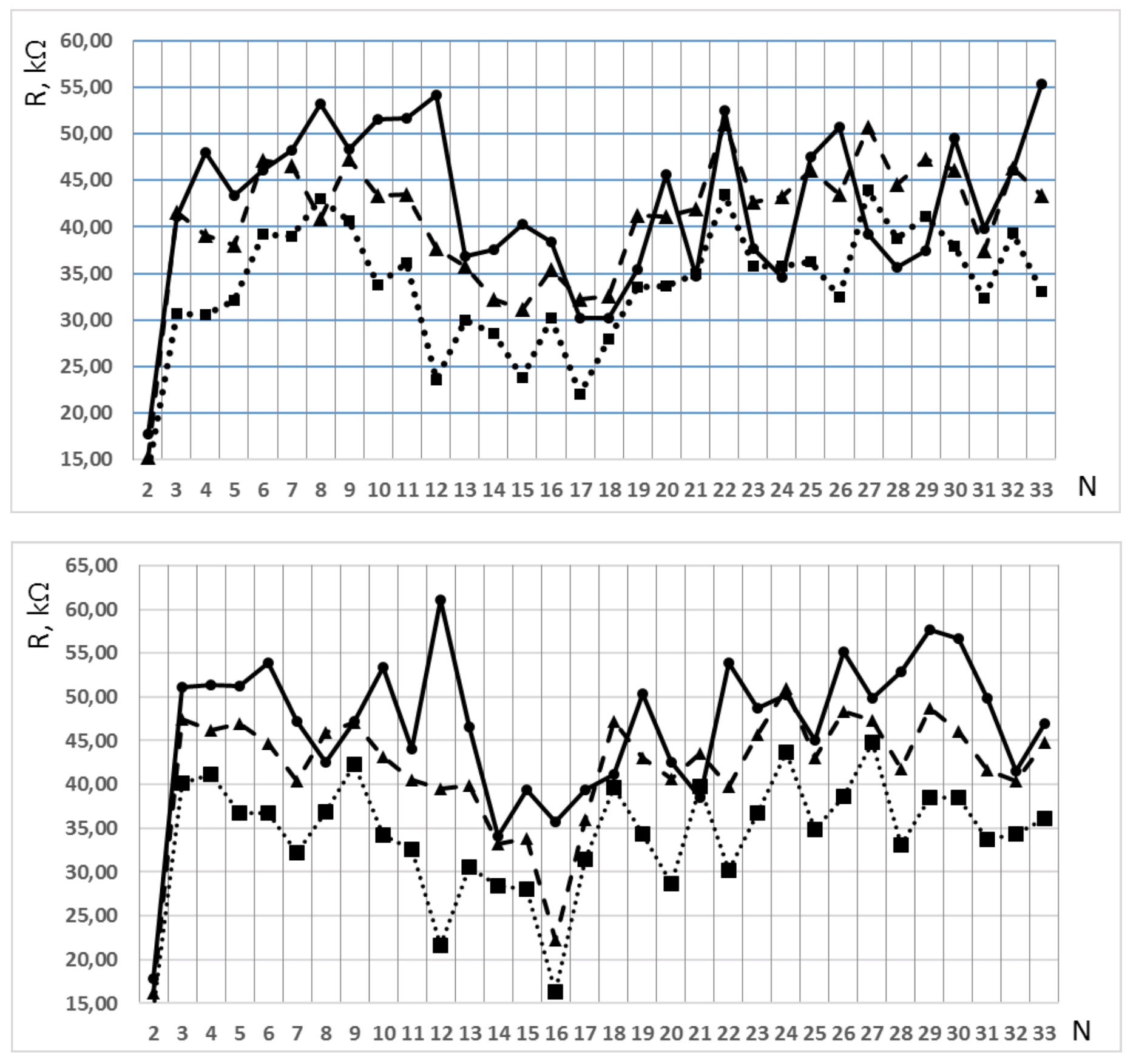
Figure 2. (upper) – The pattern for resistance of centesimal potentiated dilutions of diclofenac, set M; (bottom) – The pattern for parallel preparation, set #M. N-is the number of dilutions. The accuracy does not exceed the size of the points. Lines for clarity connect the experimental points. The curves are measurements a day after the preparation of the samples (solid), 14 days later (dashed), 30 days later (dotted).
One can see from Table 1 the strong correlation between patterns measured up to 30 days after preparation of the samples. Correlation coefficients decrease in time; however, they remain high. Statistical significance for correlation between patterns 1-30 and #1- #30 is equal to p<0.01, and all others have p<0.001. Statistical significance for cross correlation between patterns M and #M for 30 days is equal to p<0.001. Table 2 shows correlation coefficients between partial patterns divided into two parts with N=2-15 and N=16-33. Correlation coefficients decrease in time in both partial patterns. The first partial pattern (N=2-15) has high correlation coefficients that remain significant up to 30 days, but the second partial pattern (N=16-33) has smaller correlation coefficients that become insignificant on the 30th day after the preparation of samples.
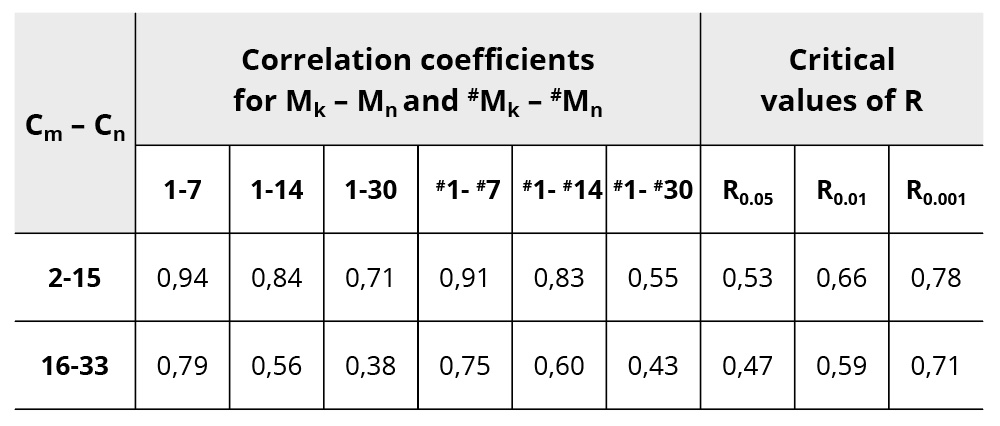
Table 2. Correlation coefficients R between partial patterns M (2-15 and 16-33 steps of dilution). Critical coefficients for correlation coefficients with corresponding degrees of freedom are given.
What is the reason for such a strange non-classical behavior of highly diluted solutions? There is no exact explanation for the phenomenon, but there are certain hypotheses. Nanobubbles called bastons are spontaneously formed and always present in water (Bunkin et al. 2015). Vigorous shaking of the solution leads to the formation of many micro- and nanobubbles, which, when collapsing, release a lot of energy, which leads to the appearance of reactive oxygen and nitrogen forms in the solution. Several papers confirm this assumption. Stable bubbles with an average size of 600 nm appear in vessels with water subjected to vibrations with an amplitude of 5 mm and a frequency of 30 Hz. At the same time, there is a “blue” luminescence that is typical for sonoluminescence. The amount of hydrogen peroxide and hydroxyl radically increases with the time of mechanical action (Gudkov et al. 2020; Bruskov et al. 2020). The formation of reactive oxygen species under the influence of weak external forces and fields leads to the appearance of long-term chemical transformations, including cyclic ones (Gudkov, 2012).
There is no complete clarity in the mechanisms of the described observations. About 40 chemical reactions involving reagents and products of oxygen-hydrogen molecules are known (Ignatiev et al., 2008). Among them there are both very fast and very slow reactions, which leads to a long evolution of the system (Bingi and Sarimov, 2014; Belovolova et al. 2014). In water saturated with atmospheric carbon dioxide, hydrogen carbonate anions can act as electron donors and affect the course of conjugated chain electron-radical reactions (Voeikov, 2012). The initiator of these processes can also serve as natural sources of ionizing radiation, leading to the appearance of hydrated electrons. The changes of conductivity caused by the changes of the charge carriers in solution. The analogous non-monotonic conductivity of diluted solutions was observed earlier and explained by formation of stable water nanostructures (Elia and Niccoli, 2004; Elia et al. 2014). This point of view is more a hypothesis than a proven fact since the structure of inhomogeneities in solutions has not been established and their characteristics are not known. Most likely, the heterogeneity of aqueous solutions should be explained by the presence of clusters of nanobubbles and the changes in conductivity by the appearance of reactive oxygen species and their evolution.
Conclusions
The complex non-monotonic pattern of conductivity in a wide range of dilutions accompanied by intensive mixing indicates that the result is determined not by the concentration of the solution, but by the procedure of its preparation. Intensive bubble formation is observed in such solutions. The collapse of these bubbles leads to the appearance of chemically active forms of oxygen, nitrogen and decomposition products of water, which together with the dissolved substance form a complex chain of chemical reactions. Each subsequent dilution with potentiation changes the concentrations of reacting components, which leads to significant variations in conductivity, which results in a complex pattern over the entire dilution range, including the region of non-existent concentrations of diclofenac. The task for the future is to determine the real participants of charge transfer in such systems.
Discussion with Reviewers (DWR)
Reviewer: What is the rationale for using diclofenac rather than another molecule? Could you maybe add a sentence to clarify this?
Author: Diclofenac is a very popular medicine that reduces inflammation and pain. It is used to treat aches and pains, as well as problems with joints, muscles, and bones. Diclofenac is presented in tablet, capsule, suppository, gel, plaster, injection and eye drop form. However, it is toxic in large doses and with prolonged use. Earlier on, for the first time, we found a high correlation between physical properties and the physiological response of highly diluted solutions (Lobyshev et al. 2005). Now we want to find a high dilution of diclofenac, which will have the same activity as at high concentration based on the results of a physical experiment. The biological experiment will be carried out at the next stage.
Reviewer: Both M and #M are dilutions series of diclofenac and therefore you cannot discard the possibility that the effects observed are due to the starting substance. This seems to contradict your sentence in the abstract: ”This means that the result does not depend on the concentration of the solute, but on the sample preparation procedure.”
Author: I agree that any substance including diclofenac will influence the pattern of resistivity. I want to emphasize that the patterns of probes prepared in parallel (M and #M) are very similar, but the patterns of probes prepared on different days may have much less correlation coefficient due to unspecified reasons. This is not surprising, since the processes of self-organization in complex systems strongly depend on small variations in the initial parameters, i.e., the procedures of sample preparation, including the state of always non-equilibrium water.
Reviewer: You mention measurements over the 20-10 MHz but, as far as I understand, you only present results obtained at 100 kHz. This needs to be made clearer.
Author: We did not observe dispersion effects in a wide frequency range except for the polarization of electrodes at frequencies below 30 kHz. Due to technical reasons, we can say that dielectric constant of solutions is very stable within 0.2% at 100 kHz and it does not depend on variable conductivity. At lower frequencies, the measured capacity greatly increases, and this is the result of polarization but not dielectric constant of the liquid probe. Unfortunately, I found this mistake in several authors. At 100 kHz frequency, the role of polarization is absent with great accuracy and does not have an influence on complex impedance measurements of the solution. Technical details including the whole spectra and electrical equivalent schemes are published in Lobyshev (2019).
Reviewer: Did you think of the chance to probe the hypotheses according to which reactive oxygen and nitrogen species play a role (in the trend of resistance with the number of succussion and dilution), by the measurement of the Oxy-Reductive potential of the sample..? Could it give some insight about what is happening inside there…?
Author: Yes. We thought about it but prefer to use more specific methods in future works.
Reviwer: How would you qualitatively, heuristically, update your hypotheses by taking into account the proven bi-phasic nature of liquid water, were a coherent fraction – organized in dynamic aggregates about 50-70 nm large – to co-exist with a gas-like fraction, and where solutes give rise to a complex interplay with the two phases of water? (Keeping the role of nanobubbles valid, of course.)
Author: Unfortunately, the general QED theory cannot presently predict anything for specific systems. This was clearly explained in the answers to questions by Giuseppe Vitiello at WATER CONFERENCE 2018. In addition, the composition of these coherent regions is still unknown (pure water does not exist at all), so it is difficult to talk about their interaction with active oxygen and nitrogen forms.
References
Belovolova LV, Glushkov MV, Vinogradov EA (2014). Influence of dissolved gases on highly diluted aqueous media. Biophysics 59: 524-530.
Binhi VN, Sarimov RM (2014). Relaxation of liquid water states with altered stoichiometry. Biophysics 59: 515-519.
Brown SL, Van Epps DE (1985). Suppression of T lymphocyte chemotactic factor production by the opioid peptides beta-endorphin and met-enkephalin. J Immunol 134: 3384-3390.
Bruskov VI, Chernikov AV, Ivanov VE, Karmanovaa EE, Gudkov SV (2020). Formation of the Reactive Species of Oxygen, Nitrogen, and Carbon Dioxide in Aqueous Solutions under Physical Impacts. Phys Wave Phenom (2020) 28: 103–106.
Bulavin LA, Gotsul´skii VY, Malomuzh NP, Chechko VE (2016). Relaxation and Equilibrium Properties of Dilute Aqueous Solutions of Alcohols. Russ Chem Bull. 65: 851-876.
Bunkin NF, Shkirin AV, Babenko VA, Sychev AA, Lomkova AK, and Kulikov ES (2015). Laser Diagnostics of the Bubston Phase in the Bulk of Aqueous Salt Solutions. Phys Wave Phenom 23: 161–175.
Burlakova EB, Grechenko TN, Sokolov EN, Terekhova SF (1986). The effect of inhibitors of radical lipid oxidation reactions on the electrical activity of an isolated neuron of a grape snail. Biophysics 31: 921-924.
Burlakova EB (1999). Features of the action of ultra-low doses of biologically active substances and low-intensity physical factors. Russ. Chem. J XLIII: 3-11.
Elia V, Niccoli M (2004). New Physico-Chemical Properties of Extremely Diluted Aqueous Solutions. J Therm Anal Calorim 75: 815-836.
Elia V, Ausanio G, Gentile F, Germano R, Napoli E, Niccoli M (2014). Experimental Evidence of Stable water Nanostructures in Extremely Dilute Solutions at Standard Pressure and Temperature. Homeopathy 103: 44-50.
Epstein OI (2008). Ultra-small doses (the history of one study). Moscow, RAMS Publishing House, 2008, 336 p (in Russian).
Epstein OI (2013). The phenomenon of release activity and the hypothesis of “spatial” homeostasis. Uspekhi of Physiological Sciences 44: 54-76 (in Russian).
Gudkov SV, Penkov NV, Baimler IV, Lyakhov GA, Pustovoy VI, Simakin AV, Sarimov RM, Scherbakov IA (2020). Effect of Mechanical Shaking on the Physicochemical Properties of Aqueous Solutions. Int J Mol Sci 21, 8033.
Gudkov SV, Karp OE, Garmash SA, Ivanov VE, Chernikov AV, Bruskov VI, Monokhin AA, Astashev ME, Yaguzhinsky LS (2012). Generation of reactive oxygen species in water under exposure to visible or infrared irradiation at absorption bands of molecular oxygen. Biophysics 57: 1-8.
Hahn M, Krickl S, Buchecker T, Jost G, Touraud D, Bauduin P, Pfitzner A, Klamt A, Kunz W (2019). Ab initio prediction of structuring/mesoscale inhomogeneities in surfactant-free microemulsions and hydrogen-binding-free microemulsions. Phys Chem Chem Phys 21: 8054 -8066. DOI: 10.1039/c8cp07544a
Ignatiev AN, Pryakhin AN, Lunin VV (2008). Numerical simulation of the kinetics of ozone decomposition in an aqueous solution. Russ Chem Bull 57: 1172-1178.
Krickl S, Touraud D, Bauduin P, Zinn T, Kunz W (2018). Enzyme activity of horseradish peroxidase in surfactant-free microemulsions. J Coll Int Sci 516: 466-475. https://doi.org/10.1016/j.jcis.2018.01.077
Lobyshev VI, Ryzhikov BD, Shikhlinskaya RE, Mazurova TN (1994). Intrinsic Luminescence of Water and Heavily Diluted Solutions of Dipeptides, Biophysics 39: 557-563.
Lobyshev VI, Shikhlinskaya RE, Ryzhikov BD (1999). Experimental evidence for intrinsic luminescence of water, J Mol Liquids 82: 73-81.
Lobyshev VI, (1999). Long scale evolution of luminescent properties of water and glycyltryptophan solutions, influence of UV irradiation, In: Optical Diagnostics of Biological Fluids IV, Ed.: Priezzev AV, Toshimitsu Asakura, Proc SPIE 3599: 52-57.
Lobyshev VI, Tomkevich MS, Petrushanko IYu (2005). Experimental Study of Potentiated Aqueous Solutions. Biophysics 50: 416-420.
Lobyshev VI (2019). Dielectric Characteristics of Highly Diluted Aqueous Diclofenac Solutions in the Frequency Range of 20 Hz to 10 MHz. Phys Wave Phenom 27: 119–127. https://doi.org/10.3103/S1541308X19020067
Lobyshev VI (2021). Evolution of high-frequency conductivity of pure water samples subjected to mechanical action: effect of a hypomagnetic field. Phys Wave Phenom 29: 98-101. https://doi.org/10.3103/S1541308X21020084
Molochkina EM, Ozerova IB, Burlakova EB (1999). The effect of phenosan and exogenous acetylcholine on acetylcholinesterase and the lipid peroxidation system in the membranes of brain cells. Russ Chem J XLIII: 63-71.
Palmina NP, Maltseva EL, Pynzar EI, Burlakova EB (1999). Modification of protein kinase activity with ligands in ultra-low concentrations. The role of proteinase C and its effectors in the process of peroxidation. Russ. Chem. J XLIII: 55-63.
Perchikhin YuA, Shangin-Berezovsky GN, Rappoport IA (1977). Changes in the activity of aminotransferases under the influence of N-nitroso N-diethyl urea on blood serum. Chemical mutagenesis and the creation of intensive-type varieties. Moscow, Nauka 1977, p. 263 (in Russian)
Ryzhkina IS, Murtazina LI, Kiseleva YuV, Konovalov AI (2009). Properties of supramolecular nanoassociates formed in aqueous solutions of biologically active compounds in low or ultra-low concentrations. Doklady Phys Chem 428: 196–200.
Ryzhkina IS, Kiseleva YuV, Mishina OA, Timosheva AP, Sergeeva SYu, Kravchenko AN, Konovalov AI (2013). Correlations between the self-organisation, physicochemical properties and biological activity of Mebicar in dilute aqueous solutions. Mendeleev Commun. no.23: 262-264.
Ryzhkina IS, Sergeeva SYu, Murtazina LI, Akhmetzyanova LR, Kuznetsova TV, Knyazev IV, Petrov AM, Dokuchaeva IS, Konovalov AI (2019). Features of self-organization and biological properties of solutions of citric and succinic acids in low concentrations. Russ Chem Bull Intern. Ed. 68: 334—340.
Ryzhkina I, Murtazina L, Gainutdinov K, Konovalov A (2021). Diluted Aqueous Dispersed Systems of 4-Aminopyridine: The Relationship of Self-Organization, Physicochemical Properties, and Influence on the Electrical Characteristics of Neurons. Frontiers in Chemistry 9 article 623860 https://doi.org: 10.3389/fchem.2021.623860
Yamskova VP, Modyanova EA, Reznikova MM, Malenkov AG (1977). Highly active tissue-specific adhesive factors of the liver and lung. Mol Biol 11: 1147-1154.
Yamskova VP, Modyanova EA, Levental VI, Lankovskaya TP, Bocharova OK, Malenkov AG (1977). Tissue-specific macromolecular factors from the liver and lung: purification and effect on the mechanical strength of tissue and cells. Biophysics 22: 173-175.
Voeikov VL, Vilenskaya ND, Ha DM, Malyshenko SI, Buravleva EV, Yablonskaya OI, Timofeev KN (2012). The stable nonequilibrium state of bicarbonate aqueous systems. Russ J Phys Chem A 86: 1407-1415.
Wang Y, Zhao Z, Yuan WZ (2020). Intrinsic luminescence from nonaromatic biomolecules. Chem Plus Chem 85: 1065-1080. doi: 10.1002/cplu202000021
Zaitsev SV, Sazanov LA, Koshkin AA, Sud’ina GF, Varfolomeev SD (1991). Respiratory burst inhibition in human neutrophils by ultra-low doses of [D-Ala2] methionine. FEBS Lett 1991, vol. 291: 84-86.
