 Magnetic Effects on the Polarization Parameters of Free Electrons in Quantum Field Theory
Magnetic Effects on the Polarization Parameters of Free Electrons in Quantum Field Theory
Claudio Verzegnassi, AMeC (Association for Medicine and Complexity), Trieste, Italy
Roberto Germano*, PROMETE_ CNR Spin Off, Napoli, Italy
*Corresponding author
Submitted: February 6, 2019; Revised: August 5, 2019; Accepted: October 7, 2019; Published: December 17, 2019; Available Online: December 17, 2019
Abstract
We computed, in the Quantum Field Theory approach, the effects of a weak magnetic field on the two quantities that we defined as polarization parameters of a system of free electrons. We show that these two parameters determine the calculable change of the energy of the system under a magnetic field. We show that a magnetic field can also change the values of these parameters, leading to possibly observable effects on the free electron system. We propose performing an experimental test of the previous statement, assuming the existence and the properties of the Pollack “fourth phase of water.”
Discussion
In two recent papers [1, 2] we have computed the effects of a magnetic field on the energy and on the spin of a system of free electrons in a Quantum Field Theory treatment. The theoretical expression of the Hamiltonian H and of the spin![]() have been derived from the Dirac Lagrangian and have the following form:
have been derived from the Dirac Lagrangian and have the following form:
1) 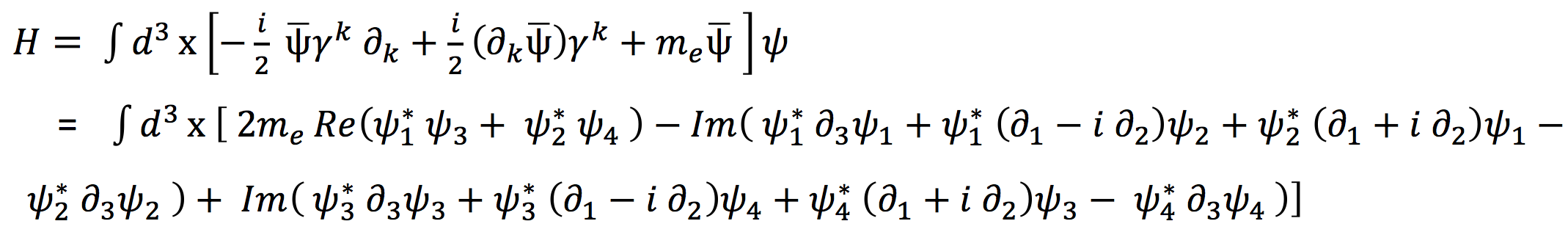
2) ![]()
3) 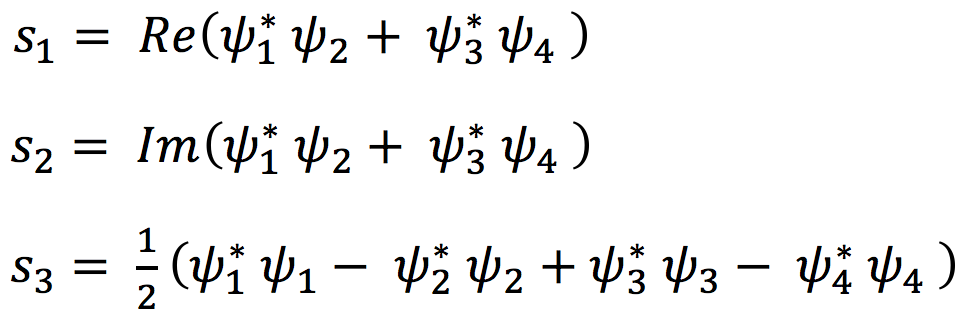
In the previous equations 1 and 3 the four components ψ1, ψ2, ψ3, ψ4, of the electron field ψ appear under the integral.
The Coherent QED (Quantum ElectroDynamics) ab initio calculations of E. Del Giudice, G. Preparata, G. Vitiello, R. Arani et al. [14, 15, 16, 17] show that at room temperature liquid water is a mix of coherent (Coherence Domain: CD) and incoherent (like a dense gas) water molecules, the coherent state being the superposition of the ground state and of an excited state of the H2O molecule. The statistical weight of these two states is such that 0.13 quasi-free electrons per molecule, 900 000 quasi-free electrons for each CD, are present [23].
These theoretical ab initio findings, as well as the experimental findings of one of us (RG) on electricity extraction from bi-distilled water by twin electrodes [6, 7, 8] – the Oxhydroelectric Effect – evidence that water coherence domains are collecting low grade energy from the environment, converting it into high grade energy able to perform external work.
From this point of view, the liquid water is peculiar since the molecule excited state involved in the coherent oscillation has an energy of 12.06 eV, a bit lower than the ionization threshold (12.60 eV). This means that only a small amount of energy (12.60 – 12.06) eV = 0.54 eV is enough to release an electron. Consequently, the coherent fraction of liquid water, unlike chaotic non–coherent fraction, is a reservoir of quasi-free electrons that can be easily released out by quantum tunnel effect or by small perturbations able to induce electronic excitations in the non-coherent molecules surrounding the CDs.
The introduction of a magnetic potential ![]() produces changes in Eqs. 1 and 2 that have been computed according to the Dirac prescription ∂µ→ ∂µ-i|e|Aµ . In the non-relativistic limit (NRL) that we have considered (ψ1, ψ2, ψ3, ψ4) we have obtained the following results:
produces changes in Eqs. 1 and 2 that have been computed according to the Dirac prescription ∂µ→ ∂µ-i|e|Aµ . In the non-relativistic limit (NRL) that we have considered (ψ1, ψ2, ψ3, ψ4) we have obtained the following results:
4) ![]()
where e is the electron charge
5) ![]()
where ![]() is defined as
is defined as
6) ![]()
where ![]() are the conventional gamma matrices.
are the conventional gamma matrices.
Starting from Eqs. 1 and 5 it is then computed the expectation value of the changes in energy and spin for a single electron state, in particular for a free electron state of momentum ![]() = (0, 0, k3) along the z axis. The state has been taken as a linear superposition of spin eigenstates
= (0, 0, k3) along the z axis. The state has been taken as a linear superposition of spin eigenstates
7) ![]()
where the numbers λ+, λ– satisfy the normalization condition
8) ![]()
From the calculation performed in Ref. 1, 2 it turns out that the average magnetic effects on the energy H = < ∆Α⃗ H > and the spin component S3 = < ∆Α⃗ S3 > are determined by the values of the λ+, λ- parameters. In particular, for the energy effect we find:
9) ![]()
where E is the free electron energy, and <A1>, <A3> are the average values of the magnetic potentials A1, A3 inside the volume V of space sizes d1, d2, d3 where the magnetic field interacts with the electron state. For the Spin S3 component, given the value of the momentum ![]() = (0, 0, k3) of the considered state, we can identify the variation of S3 with the variation of the helicity h, since in our case
= (0, 0, k3) of the considered state, we can identify the variation of S3 with the variation of the helicity h, since in our case
10) 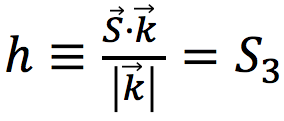
This effect has been computed in Ref. [2] and reads:
11) 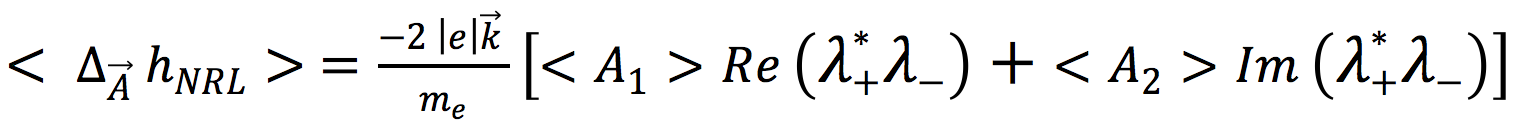
As one sees from Eq. 9, the extra term that the energy H acquires under the effect of the magnetic field can be not hermitian for complex λ+, λ– values. To avoid such a possibility we shall retain real λ+ and λ– values from now on. We shall also consider the effect of a constant magnetic field B of components
12) ![]()
Under these assumptions we obtain the following results:
13) ![]()
14) ![]()
As one sees the direction of the magnetic field is relevant for the determination of the effects. In Ref. 1, 2 we have considered the particularly simple case of a magnetic field ![]() that has the same direction as the electron momentum, i.e.,
that has the same direction as the electron momentum, i.e.,
15) ![]() = (0, 0, B3)
= (0, 0, B3)
In this case one find the special effects
16) ![]()
17) 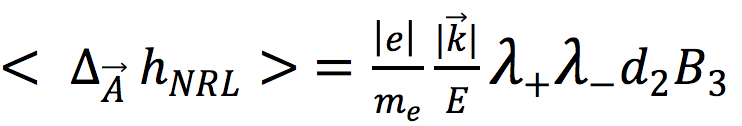
As one notices, one has in this case the exact connection
18) 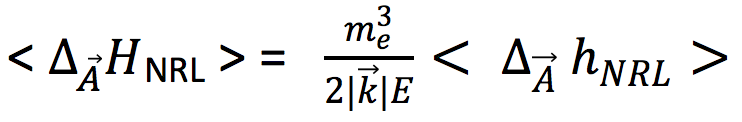
that can be derived from Ref. 1, Eqs. 8 and 13.
Having derived the mentioned results Eqs. 13, 14 two relevant questions arise. The first is that of whether our results, valid for a single free electron, can be generalized to a system of free electrons. This point is discussed in Ref. 1 and a possible solution is given, that assumes that all electrons have the same λ+, λ– parameters. In the case of a magnetic field that has the z axis direction, an extra special feature is that both energy and helicity effects are proportional to the same quantity λ+, λ–. We will give to this quantity a name:
19) PI ≡ Polarization Index.
In conclusion, we can rewrite e.g. our Eq. 17 in the following way:
20) 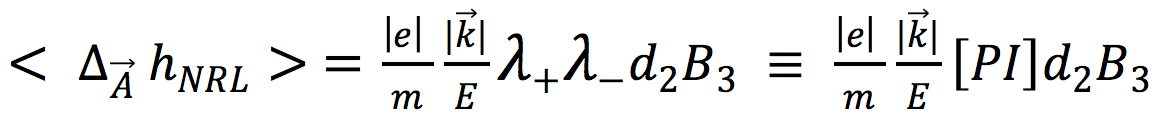
which explains why we called Polarization Index (PI) the product λ+, λ– , which fixes the variation of helicity under the effect of a magnetic field.
In fact, a magnetic field can also change the value of the Polarization Index (PI). The relevant fact is that this change does not depend on the previous value of PI, and is only fixed by the magnetic field that is applied. To derive this conclusion, we start from the fact that, we can simply verify that the average value of h in the state ψ(k ⃗ )> defined by Eq. 7 is:
21) 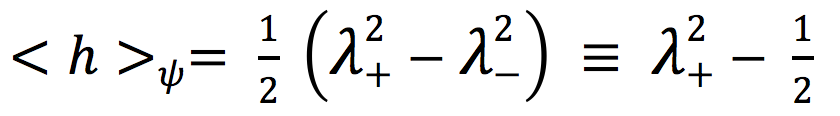
The effect of the magnetic field Β ⃗ = (0, 0, B3) on the helicity is given by Eq. 14. Using Eq. 8 gives
22) 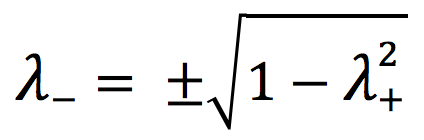
We choose a positive value for λ– and obtain
23) 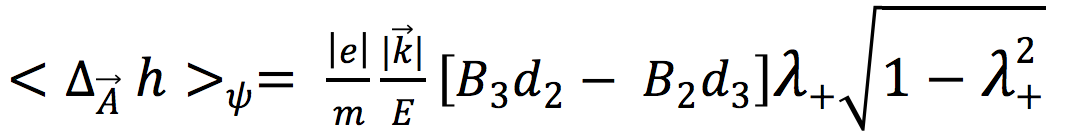
We shall call h´ the new helicity, modified by the field Β ⃗. It will be the sum of Eqs. 21 and 23.
Using our conventional notations, we shall define a modified λ+ ≡ λ–´ , such that by definition
24) ![]()
Starting from Eq. 24 we define a modified λ–´ that will be chosen as
25) 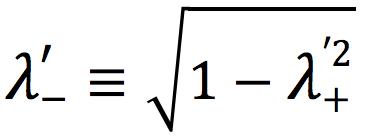
Using our previous expressions for the magnetic effects and after a number of simple steps we are led to the value of the modified Polarization Index ≡ (PI)´. This is
26) ![]()
Eq. 26 shows that the magnetic field can change the two “polarization features,” helicity h and polarization Index PI, of the considered free electron state.
The next question considered is that of which numerical sizes of these changes would be realistically observable. A proposed answer to this question uses the fact that both h and PI cannot be numerically larger in modulus than ½. Therefore we retain only magnetic effects on these two quantities larger than 0.05, that is the 10% of the one half bound, to produce a statistically meaningful change. This qualitative choice leads to the couple of disequalities, derived from Eq. 17 and 26 and considered for simplicity in the case of a magnetic field having the z axis direction, ![]() ≡ (0, 0, B3)
≡ (0, 0, B3)
27) ![]()
28) ![]()
We now choose the following parameterization:
29) d2 = α 1cm
30) B3 = β 1Gauss
The length unity of 1cm is arbitrary and it can be changed e.g. using 1micron. The reason why we retain it is that we have in mind the macroscopic size of the Exclusion Zone (EZ) introduced by Pollack [21], that can reach several hundreds of microns of depth and many cm of extent. The other unity of 1Gauss is the value of the magnetic field of small magnets that have been used in previous researches [27].
The ratio ![]() in the NRL can be identified with the electron velocity |
in the NRL can be identified with the electron velocity | ![]() |, in units of the light speed c.
|, in units of the light speed c.
Considering Eq. 28 first, we obtain now numerically, using the “God’s system” with c = 1:
31) ![]()
which gives, for the magnetic field parameter
32) 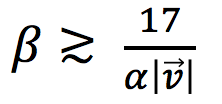
For the field intensity this gives
33) ![]()
For α ≈ 1 we would get
34) ![]()
For “not too low” electrons, |![]() |≈0.3 , this would give
|≈0.3 , this would give
35) ![]()
In full analogy, one can compute the effect on the elicity h. One finds:
36) ![]()
For values of PI ≈ 0.5 one derives for B3 the same value of Eqs. 34 and 35.
Thus, to produce visible effects, values of the magnetic field in the ≈ 50 Gauss region appear suitable in this indicative analysis.
The next question that arises is that of whether one could find a system of free electrons such that our predictions e.g. Eq. 20 could be verified. This
question can be positively answered, and the concluding part of our paper will be devoted to a presentation of our proposal.
At interfaces, thanks the attraction between the liquid molecules and the immersed surface, the water coherent structures are stabilized by boundary conditions, producing intriguing new phenomena [6, 7, 8, 18, 19, 20-26]. Separating a more coherent water from a less coherent water, we obtain something like a “water-water battery,” where the coherent water represents the negative pole and the non-coherent water is the positive pole: this asymmetry arises at the water interface with membranes, hydrophilic surfaces, microspheres, etc.
In fact, in the last 13 years, G. H. Pollack and his collaborators have reported the existence of extended regions at the boundary between liquid water and a hydrophilic surface, that they called Exclusion Zones (EZs), because the dyes dissolved in water cannot enter [21]. The depth of these EZs can be some hundreds of microns, that is a considerably wider region than any classical predictions. The peculiar properties of the water from the EZs are: higher viscosity than bulk water (about tenfold); negative electric potential (up to 150 mV) with respect to the neighboring bulk water; protons concentration at the boundary between EZs-water and bulk water; peak of light absorption at 270 nm; fluorescent when excited by 270 nm wavelength light; IR irradiation increases the depth of the EZs layer; cannot host solutes.
In fact, recent experimental finding of one of us [9, 10, 11], in V. Elia’s research group, evidenced, for the first time, micron-sized chiral supramolecular H2O aggregates in water at ambient conditions. The chiral configuration of these water organized structures are experimentally evidenced via spectropolarimetry techniques by their effect on light polarization changes: Circular Dichroism, technique that is evidencing the difference in the absorption of left-handed circularly polarized light and right-handed circularly polarized light. The aggregates were generated by physically “perturbing” pure water, iteratively immersing a hydrophilic membrane (NAFION®) in Milli-Q water, stirring the liquid, removing and drying the membrane. The Circular Dichroism spectra of the “perturbed” water resemble those of β-sheet ordered biomolecules, moreover, lyophilization of the “perturbed” water produces a ponderal solid residue.
We showed that aggregates forming in water adjacent to a hydrophilic compound may reach and sustain a stable chiral molecular configuration, and this finding was confirmed after a few months by the first observation, performed by another research group, of a chiral water superstructure surrounding DNA at ambient conditions, revealed by second-order nonlinear optical spectroscopy [12].
In order to understand better how it is possible to have so many electrons available in liquid water, a schematic overview of the liquid water features as deduced by QED is needed:
1) At room temperature, liquid water is a mixture of coherent and incoherent water ensemble of molecules; at 0°C the percentages are 50% and 50%; at 30°C they are 40% coherent and 60% incoherent, and so on with increasing temperature, up to the evaporation temperature where the fluid is purely incoherent;
2) The coherent fraction is constituted by Coherence Domains (about 0.1 micrometer in size), each CD being constituted by about 5.5 million molecules oscillating in phase with an electromagnetic field (trapped within the CD), between two energetic configurations: the fundamental one, in which electrons are strongly bound (ionization potential 12.60 eV), and an excited configuration (12.06 eV) in which one electron per molecule is “quasi-free.”
3) Considering that the coherent state is the superposition of two molecular states, the ground state (statistical weight 0.87) and the excited state (statistical weight 0.13), at each instant, 0.13 quasi-free electrons per molecule are present, that is 900,000 quasi-free electrons for each coherence domain.
Conclusions
A general result coming from the previous discussion is that one may consider the Pollack EZ water as a container of quasi free electrons. Actually, a very small energy absorption would be sufficient to make these electrons completely free. This is the first motivation of our search, which has been devoted to the calculation of special magnetic effects on such free systems.
The main idea is that the reactions of the EZ water to a magnetic field should be identical to the reactions of its free electrons component. The choice of a magnetic field was also motivated by the fact that in a very recent article [28] the reaction of EZ water to magnetic fields of opposite sign were successfully experimentally illustrated. Our calculations have been performed in the QFT approach. In this scheme, a derivation of the main results for free electrons is simple and completely fixed by the theoretical general rules. This has given all the formulae that were written in this paper, that we consider as an early approximation to a more complete result. Clearly, it would be very interesting to consider a better, more realistic approximation where the possible electron interactions among themselves and with the other charged structures are taken into account. This might reveal a dependence on the electron mass less simple that that of our Eqs. 17 and 26, introduced by collective phenomena that might improve the computed effects. The study of these possible modifications will be performed by our group in the next future. Meanwhile, in order to find a system of free electrons such that predictions could be verified, our experimental proposal is to perform experimental measurements just on these recently discovered water aggregates rich in quasi-free electrons. Methods such as Optical Rotatory Dispersion or equivalent methods, in order to understand, first of all if the right or left-handed chirality are preferential in ordinary conditions, and afterward to measure if the preferential distribution changes under an applied magnetic field. The physical possibility to connect microscopic phenomena to mesoscopic ones being opened — in this context — via the non-trivial internal energy spectrum of water CDs.
Remember, that in general, the origin of biohomochirality is still inexplicable, in fact many molecules in natural biological systems have been found to be chiral and to have the same chirality; e.g. deoxyribonucleic acid (DNA) only contains dextro-rotatory carbohydrates. We think that the challenge of understanding how mirror-symmetry breaking in liquid water may contribute to the origin as well as pervasiveness of biohomochirality, may be via the pervasiveness of the Earth’s magnetic field influence. Such a possibility is too significant not to be pursued. Moreover, the puzzling origin of the magnetic field sensitivity is almost ubiquitous in living systems, animal and plants, from unicellular to mammals, deserves to be considered in the context of these new ideas.
References
1) C. Verzegnassi, R. Germano, P. Kurian, Quantum field theory treatment of magnetic effects on a system of free electrons, Journal of Magnetism and Magnetic Materials, 449, 482-484 (2018)
2) P. Kurian, C. Verzegnassi, Quantum field theory treatment of magnetic effects on the spin and orbital angular momentum of a free electron, Phys. Lett. A, 380, 394–396 (2016)
3) R. Arani, I. Bono, E. Del Giudice, G. Preparata, QED coherence and the thermodynamics of water, Int. J. of Modern Phys. B, 139, 1813-1841 (1995)
4) G. Preparata: QED Coherence in Matter, World Scientific, Singapore, 1995.
5) L. D. Landau, The theory of superfluidity of helium II, J. Phys. (USSR) 5, 71 (1941)
6) R. Germano, E. Del Giudice, A. De Ninno, V. Elia, C. Hison, E. Napoli, V. Tontodonato, F. P. Tuccinardi, G. Vitiello, Oxhydroelectric effect in bi-distilled water, Key Engineering Materials, 543, 455-459 (2013)
7) R. Germano, et al., Oxhydroelectric effect: electricity from water by twin electrodes, Key Engineering Materials, 495, 100-103 (2012)
8) R. Germano, V. Elia, Procedure and apparatus to extract electric energy from water, Italian patent assigned to PROMETE Srl, registration N. 1411927 (2014)
9) V. Elia, T.A. Yinnon, R. Oliva, E. Napoli, R. Germano, F. Bobba, A. Amoresano, Chiral micron-sized H2O aggregates in water: Circular dichroism of supramolecular H2O architectures created by perturbing pure water, WATER, 8, 1-29 (2017)
10) V. Elia, T.A. Yinnon, R. Oliva, E. Napoli, R. Germano, F. Bobba, A. Amoresano, DNA and the chiral water superstructure, Journal of Molecular Liquids, 248, 1028-1029 (2017)
11) V. Elia, R. Oliva, E. Napoli, R. Germano, G. Pinto, L. Lista, M. Niccoli, D. Toso, G. Vitiello, M. Trifuoggi, A. Giarra, T. A. Yinnon, Experimental evidences of physicochemical changes in water by iterative contact with a natural hydrophilic polymer Cellulose: a comparison with the synthetic hydrophilic polymer Nafion, Journal of Molecular Liquids,268, 598-609 (2018)
12) M. L. McDermott, H. Vanselous, S. A. Corcelli, and P. B. Petersen, DNA’s Chiral Spine of Hydration, ACS Cent. Sci., 3(7), 708-714 (2017)
13) E. Del Giudice and G. Vitiello, Role of the electromagnetic field in the formation of domains in the process of symmetry-breaking phase transitions, Physical Review, A74, 2, 022105 (2006)
14) R. Arani, I. Bono, E. Del Giudice, G. Preparata, QED Coherence and the Thermodynamics of water. Int. J. of Modern Phys. B 9: 1813-41 (1995)
15) E. Del Giudice, G. Preparata, Electrodynamical like charge attractions in metastable colloidal crystallites, Modern Physics Letters B 12, 21: 881-5, (1998)
16) E. Del Giudice, G. Preparata, G. Vitiello, Water as a free electric dipole laser, Phys. Rev. Lett. 61: 1085-8 (1988)
17) G. Preparata, QED Coherence in Matter, New Jersey, London, Singapore, Hong Kong: World Scientific (1995)
18) A. E. Larsen and D. G. Grier, Like-charge attractions in metastable colloidal crystallites, Nature 385: 230-3 (1997)
19) E. Del Giudice, A. Tedeschi, G. Vitiello, et al., Coherent structures in liquid water close to hydrophilic surfaces, J. Phys.: Conf. Ser. 442, 012028: 1-5 (2013)
20) Q. Zhao, J. Coult, G. H. Pollack, Long-range attraction in aqueous colloidal suspensions, Proc. SPIE, 7376: 73761C-1–73761C-13 (2010)
21) J. M. Zheng, W.C. Chin, E. Khijniak, et al., Surfaces and interfacial water: evidence that hydrophilic surfaces have long-range impact, Adv. Colloid. Interface Sci. 127: 19–27 (2006)
22) G. F. Reiter, et al., Anomalous Ground State of the Electrons in Nanoconfined Water, Physical Review Letters 111(3) 036803: 1-5 (2013)
23) V. L. Voeikov, E. Del Giudice, Water Respiration – The Basis of the Living State, WATER 1: 52-75 (2009)
24) P. Kurian, A. Capolupo, T. J. A. Craddock, G. Vitiello, Water-mediated correlations in DNA-enzyme interactions, Phys. Lett. A, 382, 33–43 (2018)
25) L. Montagnier, J. Aïssa, A. Capolupo, T. J. A. Craddock, P. Kurian, C. Lavallee, A. Polcari, P. Romano, A. Tedeschi, and G. Vitiello, Water-bridging dynamics of polymerase chain reaction in the gauge theory paradigm of quantum fields, Water, 9, 339 (2017)
26) A. Capolupo, E. Del Giudice, V. Elia, R. Germano, E. Napoli, M. Niccoli, A. Tedeschi, G. Vitiello, Self-similarity properties of nafionized and filtered water and deformed coherent states, Int. J. Mod. Phys. B, 28, 1450007 (20 pages), (2014)
