 Water, The Cradle of Life via its Coherent Quantum Frequencies
Water, The Cradle of Life via its Coherent Quantum Frequencies
Hans J. H. Geesink1, Igor Jerman2, and Dirk K. F. Meijer3
1Biophysics Group, Loon op Zand, The Netherlands; 2Bion Institute, Ljubljana, Slovenia; and 3University of Groningen, Groningen, The Netherlands
Keywords: Water molecules, water clusters, quantum coherence, coherence/decoherence balance, fractal networks, Bose-Einstein Condensate, Pythagorean-scale, algorithm, semi-harmonic quantum biology, electromagnetic frequencies, GM-scale, toroidal model.
Submitted: July 15, 2019; Revised: January 23, 2020; Accepted: February 26, 2020; Published: April 16, 2020; Available Online: April 16, 2020.
Abstract
This paper addresses the question whether electromagnetic frequencies associated with pure water are similar to those of biological systems. A literature survey was performed on intrinsic frequencies of water molecules measured across the electromagnetic spectrum using various spectroscopic technologies. The registered frequencies were plotted on an algorithmic generalized music (GM) scale, described by a quantum entangled wave function, and compared with earlier detected electromagnetic frequency patterns revealed in various biological systems. The meta-analysis shows that semi-harmonic frequency patterns found in purified water are very similar to those found in biological systems. A meta-analysis of about 700 measured frequencies of pure water shows that 192 subsequent first and second derivatives of spectral frequency curves of water molecules can be precisely positioned at the proposed lines of the calculated pattern of coherent eigenfrequencies with an error of 0.45% and statistical significance of p < 0.02. A new order parameter characteristic for water molecule assembly has been revealed, which implies quantum coherency and entanglement. This is in line with the already evidenced and published universal order that we called the GM-scale. Following these findings, we may assume that water molecule assembly shows electromagnetic and electronic collective states that contain “quantum imprints or molds” for living cells. A potential explanation for this feature is that water molecules are ordered in a partially distorted tetrahedral geometry, which yields a specific network structure. Since water molecules have a comparable distribution of coherent electromagnetic field (EMF) bands to that of fluid assemblies in living cells, a resonant wave interaction is expected between the cytoplasm and surrounding water molecules. Evidence of a new quantum wave equation of coherence for water molecules has been found, that is defined as a physical principle: En= ħ ωref 2n+p 3m.
Introduction
An expectation in the biological community is that life originated in water. Water provides the medium in which all biochemical reactions take place. The importance of water to living organisms is due to its peculiar features including its properties as a solvent, its high specific heat capacity, and its high latent heat of vaporization. Water owes these unique properties to the polarity (i.e. dipole character) of its constituent molecules, which form bonds among each other as well as with other polar molecules. Biological systems exhibit macroscopic quantum properties and superconductive properties (Turner, 2016, Geesink and Meijer, 2018e). The research field of aquaphotomics (Tsenkova, 2018) uses the spectral absorption features of water in the near-infrared wavelength range to diagnose the health of a biological system. This is achieved through analysis of its spectral patterns where overtones and combined absorption bands emerge. They are used as biomarkers for the diagnosis of healthy and diseased states. The implication goes also to the cosmic dimension, where the combination of interstellar (cosmic) dust, especially in the form of phyllosilicates, and structured water provides a semi-conducting electromagnetic conduit. It could promote the quantum entanglement of microscopic (Planck level) and macroscopic (cosmic level) wave information as a connective principle in the fabric of reality (Carniello et al., 2015).
Here, water is seen as an active medium where the principle of coherent information exists through inanimate liquid systems up to highly organized organisms (Jerman, 2016). Contemporary quantum field theory not only unveils life as a profoundly electromagnetic phenomenon but also maintains that liquids such as water have unique electromagnetic properties involving coherence. This is important for life since water is a fundamental substance in biochemical processes (Preparata, 1995; Del Giudice et al., 2005, Del Giudice et al., 2010). Consequently, the potential of water to organize biological systems is also expected to play an active and essential role for any origin of life scenario. Quantum electrodynamics (QED) reveals that all molecules fluctuate in unison between two distinct configurations (the ground and the excited one) and in tune with the enveloping vacuum electromagnetic field (see Plankar et al., 2012; and Jerman, 2016 for more detail). The collective dynamics span over a region (called a coherence domain, CD) whose size is equal to the wavelength of the EM mode, λ = hc/∆E, where h is the Planck constant and c is the speed of light. Further QED considerations demonstrate that photons in the CD acquire an imaginary mass, becoming unable to propagate and appearing as the cohesion energy of the molecules (Jerman, 2016). In this way, the CD becomes a cavity for the oscillating vacuum electromagnetic field, which fuses with the field of excitable and polar water molecules. This fusion gives rise to a unique field resulting in the collective dynamics of the water molecules; they start to behave as a single (quantum-like) object.
The stability of a coherent configuration is maintained through the existence of an energy gap, which is the difference in energy between an independent (non-coherent) and correlated (coherent) molecular configuration. This implies that the coherent state is a more ordered, lower-entropy state. Therefore, the maintenance of order requires no energy (Vitiello, 2001). In this stabilized order, a quantum vacuum field is essential. At any given temperature that allows liquid water there is a proportion of water molecules in coherent domains and another in a non-coherent phase; at room temperature, a molecule of water spends around 30% of the time in a coherent domain.
Quantum electrodynamics further predicts a picture of living matter that includes a decisive role for water. Biological polymers present in the non-coherent spaces between CDs are influenced by the tails of the coherent EM fields that radiate from the CDs. According to the general theorem of electrodynamics, molecules that oscillate at the CD field frequency become strongly attracted more prone to react chemically (Del Giudice et al., 2005, Del Giudice et al., 2010). Hence, in an extended coherent region, a diffusive regime of molecules is replaced by a selective dynamic regime, where molecules recognize each other and interact on the basis of frequency codes. Biological dynamics appears, therefore, as a close interplay between electromagnetism and chemistry, where fields are able to make the molecules interact through resonance, and molecules are able to regulate the field frequency through reaction energies. According to the general scheme outlined above, water molecules in bulk are predicted to give rise to CDs with a size of around 0.1 µm (Arani et al., 1995). In biological environments, however, these CDs are presumed to give rise to extended domains of molecular complexes, reaching sizes equivalent to a whole cell or tissue (Del Giudice and Tedeschi, 2009). Since the excitable spectrum of a CD is very rich (Del Giudice, Preparata, 1998), a variety of extended domains can emerge that assume a nested (i.e. fractal) architecture (see Vitiello, 2009; Geesink and Meijer, 2017a, 2018a). Extended domains imply two important consequences: a defined size of the coherent system, and the appearance of geometrical shapes (Del Giudice and Tedeschi, 2009). In order to have precise frequency matching, the relative positions of reacting molecules must assume a specific spatial configuration, corresponding to biological structures. If the coherence stops, geometric order would break down; and the system’s size would no longer be defined, as it is primarily determined by the wavelength of an EM mode.
Coherence and entanglement may be regarded as fundamental properties of quantum domains, be they basic (simple) or extended (i.e. a coherent association of many basic domains). Their coherent oscillations represent stationary waves (i.e. relatively temporally and spatially constant) that enable constructive wave interference. With sufficient lifetime, quantum coherence is thus preserved in living cells at room temperature.
From a physical standpoint, water absorbs radiation readily throughout most of the electromagnetic spectrum. The absorption spectrum spans from the extremely short γ- and X-rays to long radio waves. It is a particularly absorbent in the UV, Mid IR, FIR and microwave region. The efficiency of water in light scattering and absorption can be quantified by components of a complex index of refraction, m(λ) = n(λ) – iκ(λ). The real index of refraction n(λ) represents the strength of scattering while the imaginary index κ(λ) represents the strength of absorption. Although n and κ are collectively called the optical constants of water, they depend strongly on wavelength (Bass, 2010) as shown in Figure 1a.
The absorption spectra of water molecules in various states can be determined by measuring quantum changes in the atomic and molecular energies because of the absorbed electromagnetic waves at vibrational, rotational and electronic transitions, all of which take place simultaneously (Figures 1a and 1b). It was found that many physical systems demonstrate discrete patterns of EM frequencies (Geesink and Meijer, 2018a).
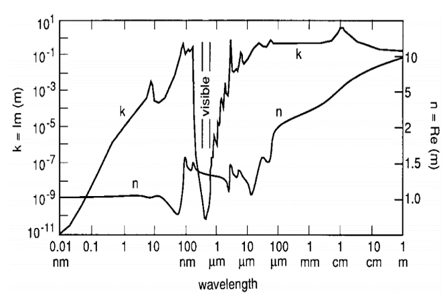
Figure 1a: The optical constants of pure water.
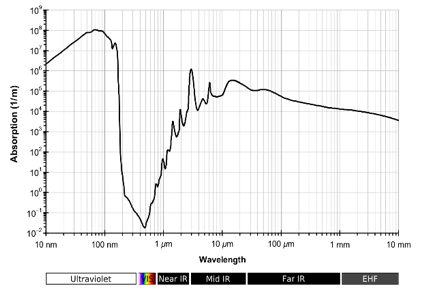
Figure 1b: Absorption spectrum of liquid water (source: Michael Bass, Handbook of Optics, Volume IV, 20).
It has been shown that electromagnetic fields affect both the degree of entanglement, and indicate that a coherent quantum entangled wave function exists (Geesink and Meijer, 2018d). A striking finding tackled the observation that life systems, as studied in 550 biomedical articles and 80 reports about entanglement and superconductivity, showed distinct EM frequency patterns. This strongly suggests that coherence, entanglement and superconductivity may be prerequisites for life. The analyzed EMF eigenfrequencies could be arithmetically scaled according to an adapted Pythagorean tuning, and that the mathematical analysis shows that the derived arithmetical scale exhibits a sequence of unique products of integer powers of 2, 3 and a factor of √2. This generalized semi-harmonic frequency spectrum reflects a discrete pilot-wave structure that can be interpreted as a “hidden variable” of David Bohm’s causal interpretation of quantum field theory (Bohm, 1952).
This paper addresses the QED consideration (described above) that pure water has a phase of coherent standing waves that can be described through a coherent quantum entanglement function and the GM scale (see Appendix 1). We focus specifically on whether the molecular resonances of pure water can be compared with resonances in and near living cells and biomolecules. To realize this aim, an extensive literature review was performed, and measured resonant frequencies of pure water over a wide wavelength range spanning the UV, VIS, NIR, MIR, and FIR were collected. These collected frequencies have been plotted on the GM-scale and compared with various EM frequencies influencing organisms as revealed in bioelectromagnetic research.
The work is presented as follows: We first describe the theoretical framework underlying semi-harmonic oscillators, with a particular focus on quantum entanglement. We follow this with a theoretical analysis of water molecules. We then discuss the role of water molecules on biomolecular processes, and propose a mechanism for water molecules’ quantum states that can explain their effect on biomolecular processes. Finally, we present the collected frequencies of pure water from the literature review and suggest a possible quantum relation.
Semi-harmonic Quantum Oscillators
Rotational, vibrational and electronic spectroscopies are used to understand the complexity of biological systems and to identify molecular mechanisms (Bloino, 2015). Until now, vibrational computations were mainly performed using the double harmonic approximation, and some scaling methods to incorporate anharmonic transitions.
Beneficial (green) and detrimental (red) biological frequency data
The inclusion of anharmonic contributions can provide a more realistic spectral pattern including the presence of chiroptical spectra, where anharmonic effects are modulations of the observed harmonic band-shapes. Within this context, we shall deal with the framework of generalized first- (1:2) and second-order (2:3) resonances (Bloino, 2015; Geesink and Meijer, 2018a).
Based on these first- and second-order resonances, a biophysical GM scale has been proposed that reveals which electromagnetic eigenfrequencies are beneficial or detrimental to living cells. The electromagnetic eigefrequencies range from one-tenth of a Hertz to a PetaHertz, and show a pattern of 12 discrete bands positioned on a Pythagorean frequency scale (Geesink and Meijer, 2018a). This finding stems from an analysis of about 500 articles published from 1950 to 2017, dealing with either endogenously measured or exogenously applied EM oscillations in tissues, cells, and biomolecules. We found that the beneficial biological effects related to the effects of in vitro or in vivo electromagnetic stimulation (defined as coherent) could be positioned on the previously introduced range of the Pythagorean-scale (beneficial frequencies, green points in Figure 2). Frequencies just between the beneficial frequencies (defined as non-coherent, red points in Figure 2) were shown to be related to patterns of detrimental biological properties (Geesink and Meijer, 2018a, 2018d). The detected eigenfrequencies could be arithmetically scaled and the scale would exhibit a core pattern of twelve eigenfrequency functions with adjacent self-similar patterns, according to the octave hierarchy (Geesink and Meijer, 2018a).
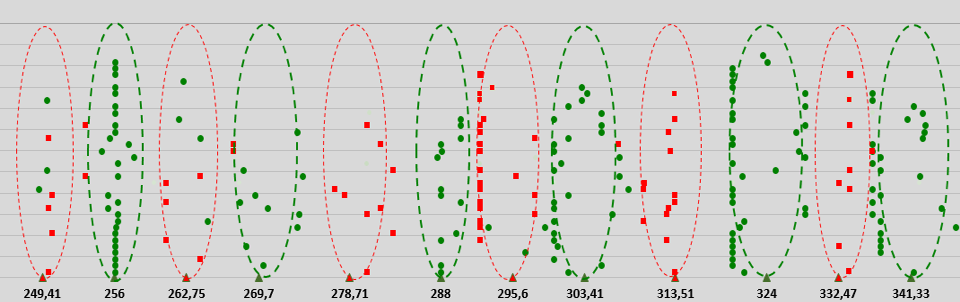
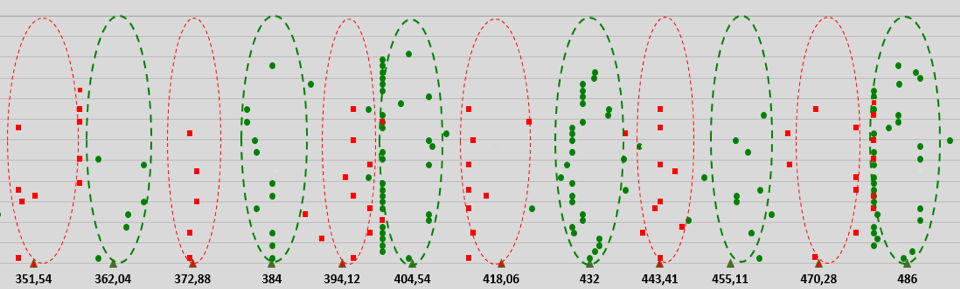
EM field frequencies (normalized) (Hz)
Figure 2: Measured frequency data of living cell systems that are life-sustaining (coherent data: green points) and detrimental for life (decoherent data: red squares) versus calculated normalized frequencies. Biological effects measured following exposures or endogenous effects of living cells in vitro and in vivo at frequencies in the bands of Hz, kHz, MHz, GHz, THz, PHz. Green triangles plotted on a logarithmic x-axis represent calculated life-sustaining frequencies; red triangles represent calculated life-destabilizing frequencies. Each point indicated in the graph is taken from published biological data and is a typical frequency for a biological experiment(s). For clarity, points are randomly distributed along the Y-axis.
All pointer states related to this coherent behavior have been described by a proposed “entangled quantum wave function,” coined by us as the generalized (GM) scale (see Appendix 1). A similar distribution pattern of EM frequencies has been found in Einstein–Podolsky–Rosen-type experiments that promote entanglement and EMF frequencies that can lower energy gaps in superconductors (Geesink and Meijer, 2018b, 2018c), as well as in the energy distribution of a range of elementary wave/particles in the standard model (Geesink and Meijer, 2017c). In general, it was concluded that the particular GM- algorithm is valid for both animate and a spectrum of coherent inanimate systems, and therefore a novel generalized physical principle was proposed. The equation describes superpositions of eigenstates that are distributions of 2/3 ratios in 1/2 ratios and therefore could be based on an adapted Pythagorean tuning and may be regarded as a specific extension of the described quantum electrodynamic theory of CDs. Decoherent oscillations that hypothetically work destructively on basic and/or extended coherent domains are described by a second equation, in which the frequencies are logarithmically positioned just in between the coherent frequencies (Geesink and Meijer, 2018a, 2018b). The discrete coherent standing wave pattern of EM wave frequencies has been mathematically expressed in a “quantum entangled wave equation”:
En= ħ ωref 2n 3m (2p)
(En : Energy distribution, ωref : Reference frequency 1 Hz, ℏ : Reduced Planck’s
constant,
n : Series of numbers: 0, 0.5, 2, 4, 5, 7, 8, -1, -3, -4,-6, -7,
m : series of integers: 0, 1, 2, 3, 4, 5, -1, -2, -3, -4, -5,
p : Series of integers: <-4, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, > +52
The core pattern of twelve eigenfrequency functions with adjacent self-similar (fractal) patterns, according to octave hierarchy, resemble the so-called pointer states. They represent quantum states that are less perturbed by decoherence than other states, as already established in QED of CDs. This particular environment allows them to exist in an objective way similar to classical states so that they remain essentially unperturbed (Zurek, 1998, Del Giudice et al., 2010).
Certain scientists proposed that quantum coherence with sufficient lifetime is preserved in living cells even at room temperature. This is based on the theory of coherent excitations in biological systems that are due to coherent correlations among oscillatory phases, as already proposed by Fröhlich (1978, 1988) and further elaborated by an Italian group of quantum field physicists (see Arani et al., 1995; Del Giudice et al. 2005). The authors also suppose that a healthy living system has a high level of coherency, while an unhealthy one shows a low level of coherency or even a high level of decoherence. The biophysical frequency patterns of discrete healthy and unhealthy biological effects have been found by the team of Tsenkova at near-infrared (NIR) frequencies (Tsenkova et al., 2000, 2004, 2018; Tsenkova, 2007; Kinoshita, 2012; Slavchev, 2015; Bazar, 2016). The particular spectral patterns of water that show overtones and combined absorption bands that arise from the NIR and the mid-infrared region are used by the authors even as a biomarker for the diagnosis of diseased states. It was Fröhlich’s idea that cancer stems from the cells that escaped the coherent intercellular regime, essential to life (Fröhlich, 1978.), thereby establishing a high level of decoherence.
Molecules that absorb near-infrared energy vibrate mainly in three modes: stretching, bending and rotating. Stretching is a continuous change in the interatomic distance along the axis of the bond between two atoms. Bending is a change in the bond angle, while rotation occurs along the axis of rotation. The most common bands arise from stretching and bending in the combination of O–H or C-H stretch, with O–H or C-H bend that occurs at different positions in the spectrum (Burns, 2007). At typical NIR-spectra, water molecules show hydrogen bonds with molecules exhibiting one OH-group (S1), two OH-groups (S2), or even without any OH-groups (S0) (Yang, 2014). The lowest normal mode frequency is known as the fundamental frequency, while the higher frequencies are called overtones. Between fundamental frequencies and overtones, so-called Fermi resonances occur in a large number of combinations that represent harmonic and anharmonic oscillations. The so-called Darling-Dennison resonance promotes the interaction between high-level overtones and a combination band and is particularly intense for bonds containing hydrogen atoms (Matthews, 2007). Overtones can occur at integer multiples of 1, 2 and 3 and combinations thereof, arising from different fundamental bands (Pasquini, 2003; Davies, 2005; Karlberg, 1989; Du, 2013), as shown in Figure 3.
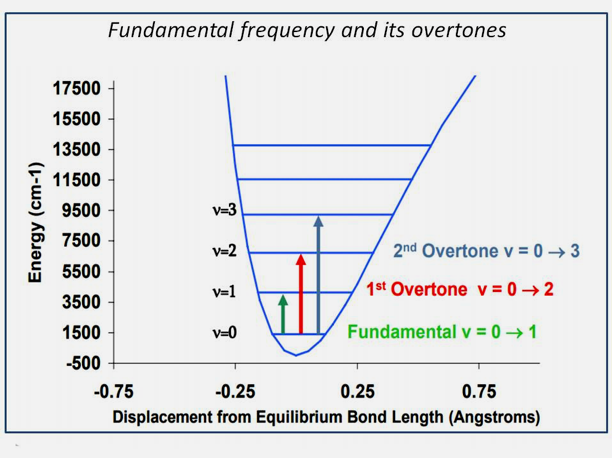
Figure 3: Fundamental frequency and overtones, see lecture N. Antaris
Water Molecules and the Hydrogen Bond
A water molecule is formed when two atoms of hydrogen bond covalently with one atom of oxygen. In the covalent bond, electrons are shared between atoms, but this sharing is asymmetric. The oxygen atom attracts the electrons more strongly than the hydrogen atoms. This gives water an asymmetrical distribution of charge. For this reason, the four-electron pairs surrounding the oxygen arrange themselves in a tetrahedral geometry (see Figure 4). As a consequence, a tetrahedral network structure of water molecules may form (see Figure 5). The two nonbonding electron pairs remain closer to the oxygen atom resulting in a distorted tetrahedral arrangement.
Molecules that have partial negative and positive charges at the opposite ends are known as polar molecules. It is precisely this polar property that allows water to separate polar solute molecules and explains why water can dissolve so many substances. Due to this difference in electronegativity, the bond dipole moment points from each Hydrogen atom to the Oxygen atom, making the oxygen partially negative and each hydrogen partially positive. The charge differences cause water molecules to aggregate (the relatively positive areas being attracted to the relatively negative areas). A single water molecule can maximally participate in four hydrogen bonds because it can accept two bonds using the electron pairs on oxygen and donate two hydrogen atoms (see also Figure 5). This attractive hydrogen bonding explains many properties of water, such as the solvent ones. Intermolecular tetrahedral structures form an open structure and display a three-dimensional bonding network, resulting in the anomalous decrease in density when cooled below 4 °C. This constantly reorganizing tetrahedral unit defines a three-dimensional dynamic network extending throughout the liquid.
In H2O, only two of the six outer-shell electrons of oxygen covalently bond with hydrogen, leaving four electrons that are organized into two non-bonding pairs. To minimize repulsions between clouds of a negative charge, the four-electron pairs surrounding the oxygen tend to arrange themselves as far from each other as possible. The result is a tetrahedral geometry in which the angle between electron pairs (and therefore the H-O-H bond angle) is 109.5°. However, because the two non-bonding pairs remain closer to the oxygen atom, these exert a stronger repulsion against the two covalent bonding pairs, effectively pushing the two hydrogen atoms closer together. The result is a distorted tetrahedral arrangement in which the H—O—H angle is 104.5°. Hydrogen atoms in water also contain protons whose magnetic moments can be parallel or antiparallel, giving rise to ortho- and para-water, respectively. The two forms are normally present in an o/p ratio of 3:1. Water is relatively transparent to visible light, near-ultraviolet light, and far-red light; it absorbs ultraviolet light, mid-infrared light, and microwaves. We envision the meaning of a distorted-like tetrahedral composition to represent a fractal structure that makes use of frequency elements as described by the proposed quantum wave function (Geesink and Meijer, 2018 e).
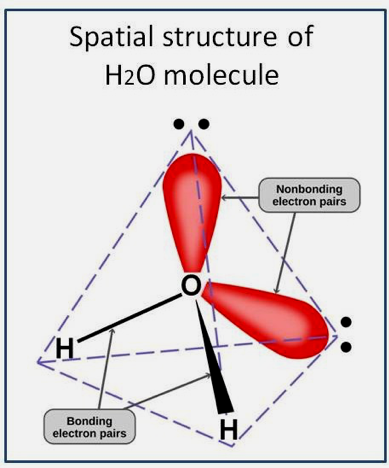
Figure 4: Two bonding and two non-bonding electron pairs.
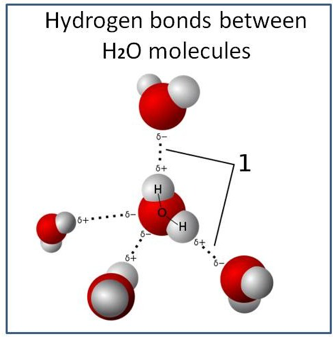
Figure 5: Model of hydrogen bonds between water molecules.
Water Clusters
The first Far-IR (FIR) spectra of gaseous water clusters were measured near 455 µm (Busarow, 1989) and the first measured intermolecular spectrum of a water cluster showed the torsional vibration of the deuterium (D2O) trimer near 112 µm (Pugliano, 1992). Much effort has been expended to describe the structure of small isolated water clusters (see Figure 6). There are two main hypotheses concerning the hydrogen-bonding of liquid water that currently divides water science. Either (a) water forms an effectively continuous three-dimensional network with the hydrogen bonds more or less distorted from their ideal three-dimensional structures, or (b) water consists primarily of a mixture of clusters of water molecules with different degrees of hydrogen-bonding in an equilibrium (Chaplin, 2007). Of course, we are speaking here of the non-coherent phase of water, therefore not ordered into coherent domains. Cyclic water clusters (H2O)n are found with n = 3 to 60 and structures of water molecules with the highest resolution have been demonstrated in the studies of Saykally (Keutsch and Saykally, 2001). Many isomeric forms seem to exist for the hexamer: from ring, book, bag, cage, to prism shape with nearly identical energy. Terahertz laser vibration-rotation-tunneling spectra and mid-IR laser spectra show several isotopomers of small (dimer through hexamer) water clusters. It has been experimentally shown that there is a size distribution of water clusters over a wide range (n=1–30) for pure (H2O) and heavy (D2O) water from the molecular level. (Ying-Ya Liu, 2018).
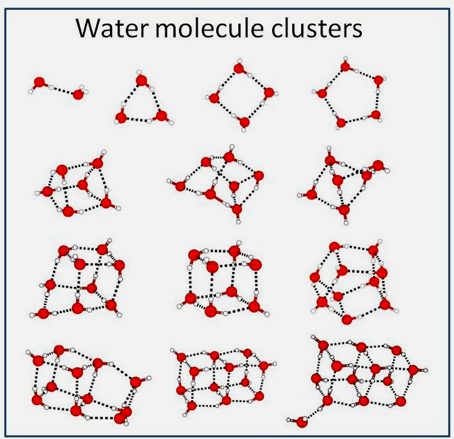
Figure 6: Water clusters, see Maheshwary et al. 2001
Water Models
Mostly, models of water are based on force field calculations, which refer to the water-pair potential. The models represent the electrostatic contribution of a) interacting point charges and b) the Van der Waals forces. Force field models rely on a certain degree of empirical findings, and several force fields exist with considerations may help in a more physically sound decomposition of the water molecules interaction energy into distinct contributions (Heßelmann, 2018). For instance, Hodges’s team (Hodges et al., 1997) showed that for several structures of a water tetramer, total four-body interactions are in most cases much smaller or even negligible compared to the three-body interactions (See Figure 6). It has been found that many-body interactions are quite significant and contribute about 13% of the total interaction energy of the water clusters. The main contribution to the many-body interactions in water clusters, with a size of up to N = 13 molecules, are higher-order polarization interactions. Scientists concluded that electron correlation effects, including dispersion interactions, are crucial for the description of the two-body interactions in water clusters. Nevertheless, they yield comparably smaller contributions to the many-body interactions (Heßelmann, 2018, Maheshwary, 2001).
Six-dimensional quantum calculations of the vibration–rotation–tunneling levels of a water dimer show that the structure calculations by symmetry-adapted perturbation theory, give a representation of the experimental high-resolution far-infrared spectrum of the water dimer (Groenenboom, 2000). Simulations reveal that although a water molecule, in general, forms two strong donor and two strong acceptor bonds, there is a significant asymmetry in the energy of these contacts. This asymmetry is a result of small instantaneous distortions of hydrogen bonds, which appear as fluctuations on a time scale of hundreds of femtoseconds around the average symmetric structure (Kühne, 2013). Quantum mechanical behavior of water can be measured by terahertz spectroscopy when it is confined to nanocavities (Gorshunov, 2013). Quantum tunneling is able to break a hydrogen bond in a water hexamer and involves the concerted breaking of two hydrogen bonds in frozen water (Richardson, 2016). When water molecules are brought between sodium layers and cobalt layers, they become superconducting under 4 K, -269°C. N-doped H2O becomes superconducting with a critical temperature of 60K, under pressure of 150GPa (Flore-Livas, 2017).
Vibrations of water molecules occur in three main modes: symmetric stretching (v1), asymmetric stretching (v3) and bending (v2) (Pegau et al., 1997; Sogandares and Fry, 1997). The vibrations are most intense at wavelengths matching the specific energy requirements of these motions and can be recognized as peaks in the absorption spectrum of pure water (Fig. 7). Because energy requirements for symmetric and asymmetric stretching are rather similar, their absorption peaks coalesce into a large absorption peak at around 3000 nm, which we may identify as the second harmonic. The bending vibrations occur at a lower energy level, resulting in an absorption peak at around 6000 nm, which one can identify as a fundamental tone or the first harmonic. Other harmonics of these vibrations occur at higher energy levels that double or triple the required energy. As a result, harmonics of the bending and stretching vibrations can be recognized as shoulders in the visible and near-infrared range. For instance, the distinct shoulders are positioned at 449, 514, 605, 742 and 972 nm (see Figure 7), and can be identified as the third, fourth, fifth, sixth and seventh harmonics, respectively, of the bending and the related symmetrical and asymmetrical stretch vibrations of water molecules (Braun and Smirnov, 1993; Pegau et al., 1997; Sogandares and Fry, 1997; Stomp, 2007). We may understand this series of peaks as a specific water vibrational signature.
From the above, the following facts can be established:
• Hydrogen bonding causes a collective ground state of liquid water.
• A hydrogen-bonded cluster in which four H2O molecules are located at the corners of an imaginary tetrahedron is an especially favorable (low-potential energy) configuration.
• H2O molecules have a tetrahedral structure at room temperature, so that, on average, each water molecule would be linked with four adjacent molecules via two donor and two acceptor bonds.
• The molecules undergo rapid thermal motions on a time scale of hundreds of femtoseconds, therefore the lifetime of any specific clustered configuration will be relatively brief.
• H2O molecules show typical frequency patterns.
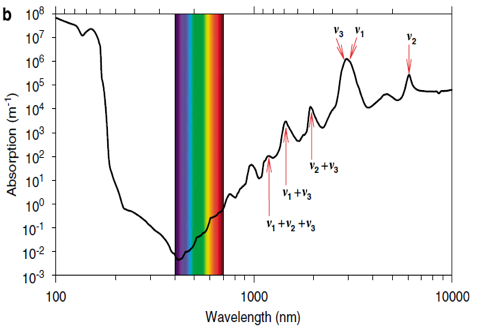
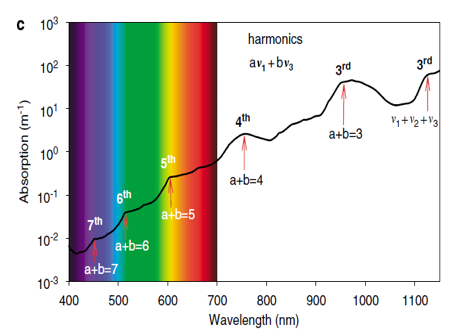
Figure 7: The three vibrational modes of the water molecule and their fundamental frequencies in liquid water: symmetric stretching (v1), bending (v2) and asymmetric stretching (v3). (b) Absorption spectrum of pure water (Hale and Querry, 1973; Segelstein, 1981; Pope and Fry, 1997). Peaks in the absorption spectrum correspond to the fundamental frequencies and higher harmonics of the combined afore mentioned vibrational modes of the water molecules. (c) Absorption spectrum of pure water in the visible and infrared region. Shoulders in the absorption spectrum correspond to the third, fourth, fifth, sixth and seventh harmonics of the symmetric and asymmetric stretch vibrations, as indicated (reference Stomp, 2007).
Pure Water
The term “pure” water has meaning in the context of a particular application or process. The distilled or de-ionized water used in the laboratory contains dissolved atmospheric gases and occasionally some silica, but the small amounts of contaminants and relative inertness of them makes these impurities insignificant for most analytical purposes. When the water of the highest obtainable purity is required for certain types of exacting measurements, it is commonly filtered, de-ionized, and triple-vacuum distilled. But even this “chemically pure” water is a mixture of isotopic species: there are two stable isotopes of both hydrogen (1H and 2H, the latter often denoted by D) and oxygen (16O and 18O) which give rise to combinations such as H218O, HD16O, etc., all of which are readily identifiable in the infrared spectra of water vapor.
Photosynthetic Pigments and Water
The photosynthetic pigments of phototrophic microorganisms cover different regions of the solar light spectrum. We can interpret the utilization of the light spectrum in terms of classical niche theory since the light spectrum offers opportunities for niche differentiation and allows the coexistence of species absorbing different colors of light. Water molecules absorb light at specific wavebands that match the energy required for their stretching and bending vibrations. Although light absorption at these specific wavelengths appears only as subtle shoulders in the absorption spectrum of pure water, due to the exponential nature of light attenuation, these subtle shoulders create large gaps in the underwater light spectrum. Model calculations show that the wavebands between these gaps define a series of distinct niches in the underwater light spectrum. These distinct spectral niches match the light absorption spectra of the major photosynthetic pigments on our planet. This suggests that vibrations of the water molecule have played a major role in the ecology and evolution of phototrophic microorganisms (Stomp, 2007).
Water in Living Cells
The cytosol, also known as the intracellular fluid or cytoplasmic matrix, is the liquid found inside cells and contains a multitude of water molecules. Although water is vital for life, the structure of this water in the cytoplasm is not well understood, mostly because methods such as nuclear magnetic resonance spectroscopy only give information on the average structure of water, and cannot measure local variations at the microscopic scale. The classic view of the water in cells is that about 5% is strongly bound by solutes or to macromolecules as the water of solvation, while the majority has the same structure as pure water (Clegg, 1984). Nuclear magnetic resonance methods have shown that, when considering the mobility of water in living cells, 85% of the cell water acts like pure water, while the remainder is less mobile and bound to macromolecules (Persson, 2008). This water of solvation is not active in osmosis and may have different solvent properties so that some dissolved molecules are excluded, while others become concentrated.
The idea that cellular water is distinct from the bulk liquid water goes back to pioneers like Gilbert Ling and Albert Szent-Györgyi in the 1960s and 1970s. Since the 1970s, many physical and physiological techniques have demonstrated that cell water behaves very differently from the bulk water. It is dynamically ordered, oriented, and exhibits restricted motion compared to water in the bulk. Similarly, interfacial water is generally recognized as being restricted in motion, more or less ordered, and has different properties from the water existing in the bulk. Hydrophilic surfaces could extend their influence over distances from the interface much larger than one or two layers (Zheng, 2006). They form an “exclusion zone,” where solutes are excluded, adjacent to a hydrophilic surface, up to hundreds of microns thick that is stable if undisturbed after formation (Chai, 2008; Zhao, 2008; Pollack 2013). Furthermore, the researchers proposed that the solute-free zone is a physically distinct and less mobile phase of water that can co-exist indefinitely with the contiguous solute-containing phase. The width of the solute-free zone is typically several hundred microns (Zheng, 2006, 2009). It also has specific electrical properties, having an excess of negative ions/electrons vs. bulk water with the dominating positive charge. It also has an alkaline pH. It has been argued that the effects of the high concentrations of macromolecules in cells extend throughout the cytosol and that water in cells behaves very differently from the water in dilute solutions (Chaplin, 2006). These ideas include strong indications that cells contain zones of low and high-density water, which could have widespread effects on the structures and functions of various parts of the cellular architecture (Wiggins, 1996).
An explanation for the anomalous properties of water comes from the two-critical-point scenario, which postulates the existence of two supercooled liquid phases, a low-density liquid (LDL) and a high-density liquid (HDL), separated by a first-order line which terminates in a critical point. The LDL and HDL phases differ in their local orientational ordering of water molecules. As seen in simulations, the molecular structure of the LDL phase has a more open and tetrahedral structure, occupying more volume. On the other hand, the HDL liquid implies a distorted tetrahedral structure characterized by higher entropy (Dandekar, 2018). In the theory of coherent domains, coherent water is of the LDL type, while the bulk water represents the HDL phase (see De Ninno et al., 2013; Del Giudice & Vitiello, 2011). Since the exclusion zone water is considered almost totally coherent – representing a huge coherent domain – it also represents the LDL phase (De Ninno et al., 2013).
Water Molecules Affect Bio-molecular Processes
Water and Protein Interactions
Thermodynamically, changes in the aqueous environment affect the stability of biomolecules. Structurally, water participates chemically in the catalytic function of proteins and nucleic acids and physically in the collapse of the protein chain during folding through hydrophobic collapse and mediates binding through the hydrogen bond in complex formation. Thus, water is a partner that potently influences the dynamics of proteins (Bellissent-Funel, 2016). Interfacial water-layers play a crucial role in protein-protein interactions. The dynamic and structural properties of water at protein interfaces have been characterized by a broadband complex dielectric constant (0.25 to 400 THz) of albumin aqueous solutions according to the experiments of Shiraga (Shiraga et al., 2016). The water molecules at the albumin interface were found to form a distorted hydrogen-bond structure due to the topological and energetic disorder of the protein surface. In addition, the intramolecular O-H stretching vibration of water (~100 THz), which is sensitive to the hydrogen-bond environment, points to a trend that hydration water has a larger population of strongly hydrogen-bonded water molecules when compared with the content of bulk water. From these experimental results, Shiraga concluded that the ‘‘strengthened’’ water hydrogen bonds at the protein interface dynamically slow the rate of reorientation of water molecules and form a less-defective hydrogen-bond network by inhibiting the fragmentation of water-water hydrogen bonds. Such a strengthened water hydrogen-bond network is composed of heterogeneous hydrogen-bond distances and angles and characterized as structurally ‘‘distorted’’ (Shiraga et al., 2016). See Figure 8.
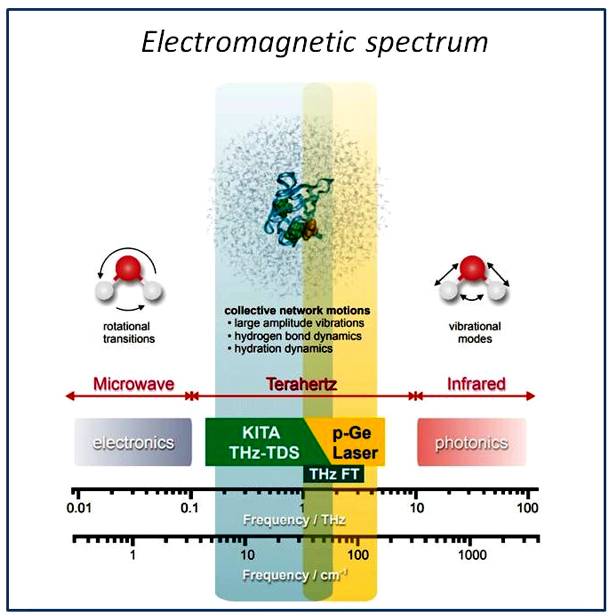
Figure 8: Electromagnetic spectrum from the microwave to the infrared region. The terahertz (THz) region is bordered by microwave and infrared spectral regions.
Molecular coupling between DNA and water, together with the accompanying process of energy exchange, have been mapped via the ultrafast response of the DNA backbone as vibrations in response to OH stretch excitation in the water molecule. The fast changes in DNA absorption after OH stretch excitation could be assigned to structural changes in the water shell in the frequency range from 940 to 1120 cm–1, which couple to the DNA through local electromagnetic fields (Liu, 2017). The energy released via hydrolysis of ATP molecules, the oscillation energy of the C = O of the peptide groups, and the different bending modes of interfacial water molecules, fit precisely the frequencies of the proposed GM-scale (see Appendix 1), respectively: 0.415 eV, 0.2073 eV and 1660–1693 cm−1 (Geesink and Meijer, 2017a).
The cellular plasma was proposed to exhibit a highly arranged 3-D geometric structure as a liquid crystal that exhibits surface interactions with macromolecular structures. The absorption spectrum between 1 THz and 10 THz of solvated biomolecules is sensitive to changes in the form of fast fluctuations of the water network. There is a long-range influence on the hydration bond dynamics of the water around protein binding sites, and water is shown to assist the molecular recognition processes (Meijer and Geesink, 2018b).
The studies by Montagnier (Montagnier et al 2015) have shown that the presence of specific DNA or RNA segments from pathogenic bacteria or viruses in aqueous solutions emit EMS (electromagnetic signals), signals that can be transduced in a non-contact way in a sort of resonance process to a different aqueous solution containing primers, DNA Polymerase, and activated nucleotides. Via this resonance, the system exhibits retrieval of the very similar DNA through PCR amplification. The theoretical explanation applies the theory of coherent water domains that retained the vibrational imprint of DNA sequences. The phenomenon was successfully repeated and further studied by the team of Tang et al. (2018). They even found the way to successfully transduce the DNA fragments of pathogenic as well as of nonpathogenic origin.
Coherent imprints induce specific polymerase activity as if the physical DNA segments were present (see Figure 9). This idea is supported by a recent report in Nature (Magar et al 2018) showing that an aqueous solution of a toxin can be ultra-diluted without losing its pharmacological activity. Both studies may imply that somehow activity is stored in coherent domains of the water molecular matrix due to the previous interaction with the specific 3-D conformation (in-formation) of these protein structures. Consequently, a cytoplasm crowded with organic and inorganic materials may act rather as a liquid crystal through the structuring of water dipoles that allow the formation of all kinds of quantum coherent wave superpositions that may be composed of fractal wave frequencies as revealed in this study.
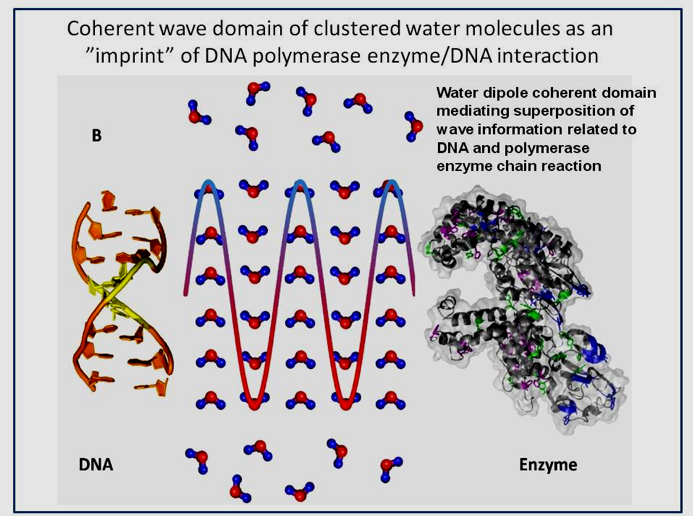
Figure 9: Picture of DNA, DNA polymerase chain reaction bridged by a coherently clustered water domain that persists after complete removal of the macromolecules from the aqueous fluid (after Montagnier et al., 2017).
Ions Dissolved in Water
It should be emphasized that water molecules in the cell are not only present in the cytoplasm, but are also situated within organelles, for instance in microtubule as atomic water channels (Sahu et al., 2013), and mitochondria that exhibit long-range EM interaction (Thar and Kühl, 2004). H2O molecules interact with DNA also structurally in the form of a chiral superstructure called the DNA chiral spine of hydration (Lake et al, 2017). These water templates produce local resonant vibrations that can be directly imaged by coherent non-linear vibrational microscopy. Such coherent domains can be stabilized by surfaces of macromolecules and membranes. The excited water is also a source of superconducting protons in the cerebrospinal fluid, which may be instrumental in the induction of conscious states in the brain (Sbitnev, 2017). Such aqueous matrices may indeed be seen as crystalline superfluids that can trap external EM frequencies from the environment to selectively orchestrate various biochemical reactions and gene expression via resonance (Ho, 2015).
Divalent cations, such as Mg2+ and Ca2+, enhance or maintain or critically deform the long-range dipole wave fields in water solutions. The reorientation of water molecules around ions and interaction with solvated ions slows down during external THz-waves excitation, shifting the absorption peak to typical frequencies (Tielrooij, 2009). The presence of different types of ions causes the stabilization of localized water clusters within the bulk of the solution as they can influence the hydrogen bonding exchanges of the affected water molecules (Musumeci, 2012). The coherence of liquid water is also affected by applied external electromagnetic waves much weaker than those allowed according to the kT threshold (Del Giudice et al., 2010). The reorientation of water molecules might take place at energy levels of less than a 100 mW/cm2, which is at a non-thermal energy level. This is supported by recent experimental work that shows that ions can influence up to 100.000 water molecules, which extend roughly 5 nm from the ion radially. The existence of a DNA minor groove spine of hydration surrounded by ions at room temperature showed that the chiral structure of biomolecules can be imprinted on the surrounding solvation structure (Dermott, 2017). All this highlights the crucial role of water as a connecting modality in the EM vibrational steering of 3-D macromolecules and the realization of the holographic memory of the cell as well as an entangled information transfer (Meijer and Geesink, 2018a).
Several models regarding frequency modes of water affecting bio-molecular processes have been proposed. Among them is the long-lasting lifetime of water structures at typical coherent frequencies may be used to store, and transfer energy (information) inside biological systems (Colleonia, 2014; Musumeci, 2012; Brizhik et al., 2001; Scordino, 2000; Lobyshev, 1999; Lobyshev, 1999; Scordino, 2000; Musumeci, 2012; Colleonia, 2014; Brizhik, 2001; Bono, 2012; De Ninno et al., 2013).
Proposed Next Generation Model of Frequency Modes of Water Affecting Bio-molecular Processes
The present authors propose that the combination of macromolecules and surrounding water molecules can be imagined as a combination of energies of quantum transitions and vibrational modes related to the interactions of photons, electrons, phonons, excitons, polarons, and solitons. According to the proposed semi-harmonic quantum model of Geesink and Meijer (2016), coherent stationary waves can be distinguished from decoherent stationary waves for living cells and biomolecules. Coherent EM field frequencies cause beneficial effects in biological systems, whereby it appears that their constructive resonance with macromolecules in the cellular system stabilizes and even reverses abnormal functioning. The coherent EM field frequencies stimulate beneficial solitons/polarons energies, which are involved in macromolecular and cellular signalling and are related to the mechanism of “Fröhlich condensation,” first hypothesized by the already mentioned physicist Herbert Fröhlich (1968, 1988).
In this process, vibrational energy is distributed over the lower- and higher-frequency vibrational modes and quantum states, mainly in the GHz and THz regions, inducing the strong quantum coherence of bio-molecules, similar to the formation of Bose-Einstein condensation as also related to superconductivity. The coherent EM field frequencies are hypothesized to promote the formation of strong quantum coherences, increasing the strength and fidelity of intra-and inter-cellular signalling. In this process, coherent oscillating domains of ordered water molecules in resonance with other macromolecules are supposed to play a central role (Meijer and Geesink, 2018b; Del Giudice and Tedeschi, 2009). The decoherent EM field frequencies should then promote chaotic non-coherent waves that show a high level of phase differences. The potential long-range resonant influence was further worked out in a study of 3-dimensional protein folding in the intact cell that can be largely influenced by the formation of coherent oscillation domains in the water in the cell interacting with the protein backbones (Meijer and Geesink, 2018b). Water shows absorption spectra in a wide spectrum of electromagnetic radiation, from the extremely short γ- and X-rays to long radio waves (Larouche, 2008) and water itself is a strong absorber of electromagnetic radiation in the infrared (IR) region (Gorshunov, 2013; Richardson, 2016).
The superconducting property of bio-photons in cell structures such as plasma-membranes, mitochondria, microtubules, and the coils of DNA, are all associated with structured water layers, and may also be instrumental in the coherent synchronization of oscillatory neuronal networks in the brain, as suggested by us (Meijer and Geesink, 2018b). A combination of scaled mixed harmonic and anharmonic frequencies for intramolecular and intermolecular modes gives a good agreement with experimental results for the water dimer and trimer (Dunn, 2006).
Validation of the Hypothesis
We will follow the analysis of Wozniak (2007) who conducted a literature search of the last 90 years for reporting measurements of the electromagnetic absorption characteristics of pure liquid water in a broad spectral region. The selected references were examined individually for specific values, or graphical or tabulated values, of the extinction coefficient k(X). The total energy of a freely moving molecule Em (L, U, J) consists of the temperature-dependent energy of its translational motion Etr, the energy of its electrons Ee(L), the vibrational energy of its atoms around its equilibrium position Evib(U), and the energy of its rotation about its various axes of symmetry Erot(J), where L, U, and J are respective quantum numbers (Wozniak, 2007). The total energy can be described as the sum of these component energies:
Eq. 1: Em (L,U,J) = Ee(L) + Evib(U) + Erot(J) + Etr
The first three—quantized—energy constituents on the right-hand side of equation (1) depend on the extent to which the molecule is excited. These take discrete values, defined by the given quantum (energy) state of the molecule or atom. The energy states of a molecule like H2O can be defined by the electronic energy (given by the quantum number L), the vibrational energy (the quantum number or numbers U), and the rotational energy (the quantum number or numbers J, while defining the absolute value of the projection of the angular momentum on to the molecule’s axis). The absorption or emission by a molecule of a photon of energy, E = hν, invariably involves its transition from one quantum state, described by quantum numbers L, U, J, to another quantum state, described by L¢, U¢, J¢ (in the general case all three quantum numbers change), following the allowed quantum mechanical selection rules. The transition of a molecule from one electronic state to another usually brings about changes in the vibrational state and the rotational state of the molecule as well. A transition during which all three types of molecular energy change as a result of the absorption (or emission) of energy gives rise to an electronic-vibrational-rotational spectrum of the absorption of electromagnetic wave energy. This is a band spectrum with a highly complex structure consisting of many spectral lines in the frequency bands of UV, VIS, NIR, MIR and FIR (Wozniak, 2007; Yasui, 2011).
The absorption spectrum of water molecules reveals a whole series of bands due to energy transitions at or between various levels. In the water molecule, since it is also anharmonic (Wozniak, 2007), energy transitions are allowed in different modes, thus complicating the analysis of their origin and characteristic features. Seven categories of such transitions, have been proposed:
• Harmonic transitions (including overtones) from the ground state
• Anharmonic transitions
• Combination transitions from the ground state
• Harmonic and anharmonic transitions between excited states
• Combination transitions between excited states
• Librations of hydrogen bonds (restricted rotations, or rocking motions)
• Cluster vibrations: involving stretching (TS) or bending (TB) of intermolecular hydrogen bonds
For this analysis of molecular water frequencies, the values of absorption coefficients were compiled from the literature that were point by point plotted graphs of measured values versus frequencies in the bands of NIR, MIR, FIR, VIS, UV, GHz and microwave regions of the electromagnetic spectrum. Smooth continuous curves for k(X) have been drawn through the plotted points (Mason, 2016; Hayashi 2015; Yasui, 2011; Wozniak 2005b, 2007; Litjens, 1999; Pope, 1997; Wielczka, 1989; Smith, 1981; Segelstein, 1981; Heller, 1974; Morel, 1974). See Figures 10, 11, 12, and the different UV, VIS, NIR, MIR and FIR graphs appendix 2.
Higher overtones of the vibrational modes can be seen as peaks and shoulders in the absorption spectrum of the visible region (Pegau, 1997). Iwamoto et al. (1987) showed that the derivative transformation of spectra is a useful method of separating multiple absorptions in broad spectral peaks of water and used this to better understand the state of water. The first and second derivative is also an efficient approach for discovering activated water absorbance bands that are not directly visible in the original spectrum (Jinendra, 2011; Bázár, 2016). The second derivative and Fourier self-deconvolution (FSD) are two commonly used techniques to resolve the overlapped component peaks of spectra. The Fourier transform infrared spectra of seaweed galactans: agar, agarose, and carrageenan, and others show that bands in the second derivative mode are sharper and more bands are resolved than in the normal spectra (Matsuhiro, 1993). To take advantage of the full power of infrared spectroscopy in structural studies of proteins, such as the amide I band, the related spectra have to be decomposed into their main component bands. This process is called curve fitting and is based on the absorption spectra and second derivative spectra (Baldassarre, 2015), see Figure 9. Therefore, we investigate these first and second derivatives of water frequency-spectra, which have been made visible by the drawn blue vertical lines (see Figures 11, 12, 13 and Graphs 1 to 17 in Appendices 2 and 3).
A total of 192 estimated subsequent first and second derivatives (blue vertical lines) were derived from about 700 measured frequencies ranging from UV to GHz, and have been made visible in the different graphs of the spectra of pure water. All the subsequent first and second derivatives can be positioned in the GM-scale by dividing these data by multiples of 2, until fitting occurs in the reference logarithmic GM-scale from 1.000 to 1.8986 Hz. See Figure 14 and Appendices 2, 3, 4 and 5.
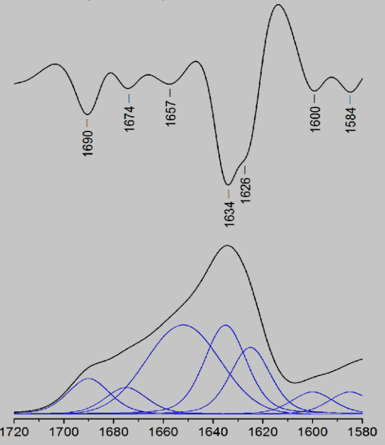
Figure 10: Example of an IR spectrum using different defined frequency parameters with initiated positions, bandwidths, and intensities. From top to bottom: second derivative and absorption spectrum (Baldassarre, 2015).
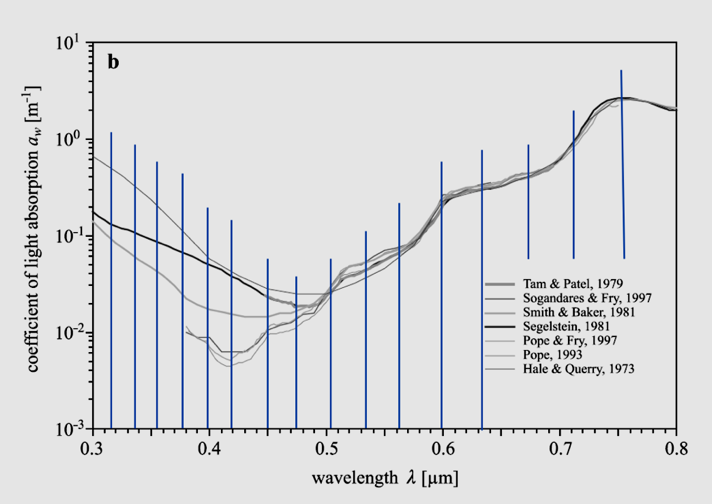
Figure 11: Absorption spectra of pure liquid water, as determined by various authors in the spectral range from the near-ultraviolet up to NIR. Reference: Wozniak, 2007. Blue vertical lines: estimated first or second derivatives by H. Geesink (2018).
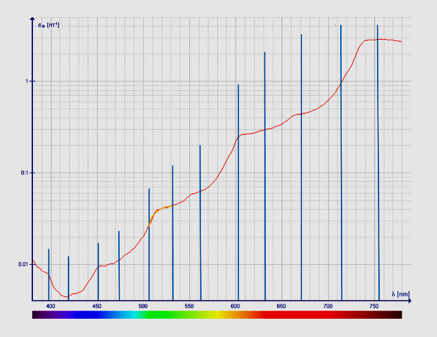
Figure 12: Absorption coefficient of pure water (380–750 nm) as measured by Pope. References: Jonasz and Miroslaw, 2007. Data of Kou L et al. 1993) and Pope R. M.; Fry E. S. (1997). Blue vertical lines: estimated first or second derivatives by H. Geesink, 2018.
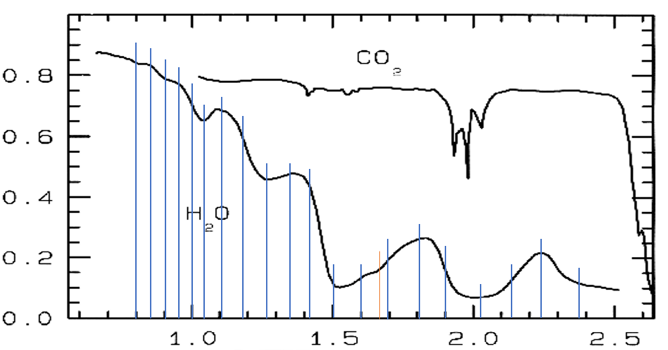
Figure 13. Reflectance NIR spectra of water, H2O, and solid carbon dioxide, CO2, from Clark et al. (1986); x-axis: wavelength in mu, y-axis: reflectance. Blue vertical lines: estimated first or second derivatives by H. Geesink (2018).
First and Second Derivatives of Frequency Spectra of Pure Water, Positioned at a Coherent Frequency-Scale
From the above, we can conclude that all first and second derivatives fit the normalized scale with high precision and a consistent pattern of 12 frequency bands for pure water can be observed (see Figure 14).
The mean deviation of 139 derived frequency data, relative to the calculated different quantum coherent frequencies according to the 12-number, is less than 0.45%, which is statistically significant at the p=0.02 level.
Secondly, we may conclude that the found pattern concerning the first and second derivatives for pure water is also in harmony with the pattern in the meta-analysis of more than 500 biomedical studies that revealed the same 12-number frequency scale. The meta-analysis shows a marked predictive value for biological effects that stabilize living cells (see the green points in Figure 2). It is striking that the derived frequency pattern of pure water assemblies is not located in the area of the 12-bands that show destabilization of living cells and biomolecules, called de-coherent normalized frequencies.
Interestingly, one typical frequency of the proposed coherent Hertz scale has already been calculated by Marc Henry (Henry, 2016). Water molecules have typical resonances at Hertz frequencies, and a typical frequency can be expressed in 3-prime-limit tuning. A calculated typical frequency of a water molecule, with a molecular weight M=18 g·mol-1, is 54 Hz. This typical frequency of a water molecule, in the center of our GM-scale, has been derived by using the mass-energy equivalence coupled to the Planck-Einstein relationship: M·c2 = h·f ⟹ f (Hz) = 2.981 × M (g·mol-1) (M is the molecular weight of water molecule, c = 299,792,458 m/s, h =6.62606959 × 10-34 J·s, and f is the frequency of a water molecule).
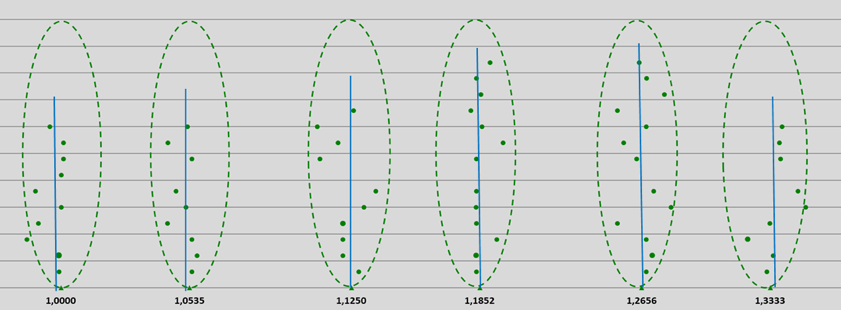
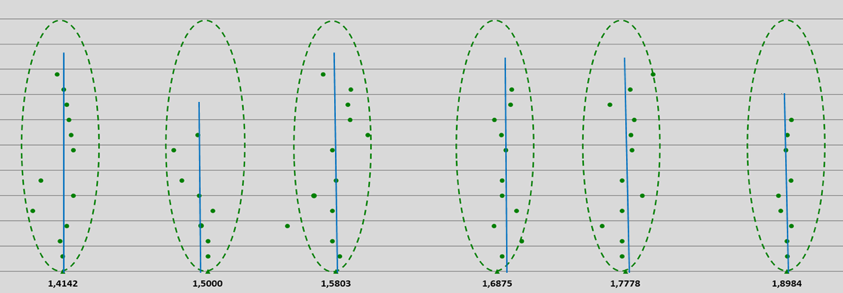
Figure 14: Pythagorean-normalized first and second derivatives of 139 spectral frequencies of water molecules obtained from literature UV, VIS, NIR, MIR, FIR and GHz data and plotted on a logarithmic scale. Each point represents a single frequency value (on a reference Hz-scale according to the proposed entangled quantum wave equation), the points are evenly spread out over the Y-axis; see also appendices 2, 3 and 4. Blue vertical lines: mean estimated first or second derivatives by H. Geesink, 2018.
Discussion
The proposed patterned frequencies involving approximate ratios of 2/3 in the living and coherent non-living systems, in general (Meijer and Geesink, 2018a), have now been supported by the present close relation between the frequencies of the surveyed water spectra. Pure water absorption spectra show precisely the same frequency pattern as found for the living cells and biomolecules within the investigated range of UV to GHz. This observation also confirms the concept of coherence in both systems; namely, both living and inorganic ones can be described by a physical principle that mediates coherence and quantum entanglement and also may have a relation with zero-point energy (quantum vacuum), as already discussed in introducing coherent water domains (Meijer and Geesink, 2018a; Jerman, 2016). This implies that the measured frequencies of water molecules may express local and non-local entanglement as described by the proposed physical principle.
The analysis of molecular water-data shows that a total of 89 different first and second derivatives of spectral frequency curves belonging to pure water can be very precisely positioned at the pointer states of a calculated pattern of coherent frequencies with an accuracy of 0.45%. The derived spectral frequencies/wavelengths match coherent frequency assemblies of energy states located at the pointer states of a 12-number frequency quantum entangled scale with high precision. It may be concluded that if molecules in pure water have a comparable nature with water molecules in living cells, then a reversible coherent interaction between living matter and water molecules may occur. Interestingly, one can find also decoherent frequency patterns, as defined by the GM-scale, when examining the spectra of waters with different typical ions dissolved in solution. The observed coherence bands for pure water also support the statement of Bloino that rotational and vibrational electronic spectroscopies can be used to understand the complexity of biological systems and to identify molecular mechanisms (Bloino, 2015). Moreover, the GM-frequency pattern applies also to the research of Tsenkova, where water IR spectral patterns are used as a biomarker for diagnosis. They show overtones and mixed absorption bands that arise mainly from the mid-infrared region.
A possible reason that all analyzed frequency patterns of pure water, characterized by spectroscopic technics from UV to GHz, fit precisely in the proposed algorithm of frequencies is that the tetrahedral geometry of the four electron pairs surrounding the oxygen of H2O is connected into a network of arranged molecules in a tetrahedral structure, and partially combined with a distorted tetrahedral structure. The same structure has been found for superconductors and smectite minerals that have octahedral and distorted tetrahedral sheets (Geesink and Meijer, 2018e). If the water in living cells forms an “exclusion zone,” where solutes are excluded next to the hydrophilic surface up to hundreds of microns thick, then this kind of water may physically behave very similarly to pure water, thereby fitting in the proposed model to sustain living cells.
Further strong confirmation of the proposed theoretical assumptions is the phenomenon of nanobacteria or more universally, nanoparticles or nanovesicles as well as organized pre-living systems (Jerman, 2017). Nanobacteria are some 5-100 times smaller structures than ordinary bacteria (~ 1 µm) and were found to accompany human life since they were discovered in all human bodily fluids and correlated to many of our diseases. While they were soon regarded as too small to function as fully living organisms by the majority of microbiologists, nanobacteria nevertheless demonstrated ability to contaminate cell cultures and, even more, they proved to be resistant to ordinary sterilizing procedures like heat and many antibiotics (Kajander, 2006; Martel et al., 2014; Yaghobee et al., 2015). They are seen as complex inorganic (mostly calcium carbonate or phosphate-based) – organic (mostly protein) biomimetic systems (Wu et al., 2013). In other words, they are highly organized, even self-propagating systems withouta trace of DNA. There is a high probability that their dynamic structure stems from multiscale coherently oscillating water together with ions and organic molecules as presented here.
There are also relations with the studies of Chladni, Ritz, Faraday, Rayleigh, and Sheldrake. Faraday and Rayleigh found that standing waves excited on surfaces of vibrated fluids oscillate at half the excitation frequency (Faraday, 1831; Rayleigh, 1883). The 2:1 ratio between the driving frequency and oscillatory response is characteristic of parametric resonance (Bechhoefer et al., 1995). The same radially symmetrical resonant wave-patterns have been found on surfaces of water fluids in circular containers, and occur at vibrational modes where whole numbers of waves play a role (Sheldrake Determinants of Faraday Wave-Patterns in Water Samples Oscillated, 2017). The wave phenomena represent a tractable analog model system for the study of morphogenesis (Sheldrake and Sheldrake, 2017). A correlation between Ritz/Chladni frequencies and the proposed algorithmic eigenfrequencies may also be found (Meijer and Geesink, 2016). Also, the measured eigenfrequencies of water resonances in circular containers (Sheldrake and Sheldrake, 2017) related to high ordered and alternating chaotic patterns in the spectrum of 50 Hz to 200 Hz show similarities with the proposed GM-scale. A first analysis shows a possible fit between both models for about 75% of the measured values.
The crucial question that remains is, how water in the cell, i.e cytoplasm, will behave in the presence of many types of macromolecules, inorganic and organic ions, etc. The solution for this is likely not to collect individual frequencies of various isolated proteins, DNA/RNA strands, channel proteins, tubulin proteins, and other cellular components, because those values depend on the composition of the environment in which the particular spectroscopic measurements have been performed. Rather, the entire integral cell should be taken into consideration, including cytoplasm, organelles, plasma membrane, and so on.
We have to approach this in a more” holistic” manner. Energy is constantly produced in the cell, and this energy is partly converted into vibrations of all cellular components, in principle, in the lowest energetic state possible (Fröhlich, 1968). However, the cell is also influenced by quantum vacuum fluctuations (called also zero point energy, ZPE), of which the proposed discrete GM-frequencies are a part of the total spectrum of quantum vacuum oscillations. A relation between coherent states of water molecules and quantum vacuum (ZPE) electromagnetic fields has been proposed (Ganeshan 2013; Sen, 2015). In principle, this field activity can excite all cellular components by resonance. Long-distance soliton-directed influence in protein folding as described by us is an apt example (Meijer and Geesink, 2018b, Melkikh and Meijer, 2018).
The question is, therefore, how to strike a balance between internal and external energetic influences. Turner suggested that all molecules in the cell drive the cellular water to certain states of vibration, but in our opinion, it may rather be a symmetrical (bidirectional) process with mutual aspects. In other words, water is the primary receiver of external EMF influences and retransmits that oscillatory energy to other dissolved substances in such a way that coherent vibration domains are formed in cellular compartments.
The EMF frequency spectrum in pure water, as revealed in the present paper, should be seen as the basic electrome- energy landscape on which the individual oscillations of macromolecules in the cell are superimposed. Each cellular component, therefore, exhibits its specific vibration state, depending on mass, charges, and in general, the degree of EM wave freedom. The latter in the cell is also stabilized by interactions with hydrated ions and the structured (quantum vacuum field (ZPE) shaped) water landscape. If wave resonance among such macromolecules is attained, phase-locked and stable quantum coherent domains of various sizes in the cell result. Such unities of shared wave frequencies can be promoted by the GM-coherent frequencies and disturbed by decoherent ones (see Figure 2).
Our proposed GM EMF-frequency spectrum has several crucial features:
a) The octave scale is fractal and therefore has deeper layers from macro (macromolecules) to the micro-level (elementary wave/particle level).
b) The vibration frequencies in the lattices of the cell belong to the phonon-quantum mode and are therefore quantized.
c) Biophotons (light particles) produced in the cells always behave in cell matrices as sound particles or phonons that can provide information transmission and facilitate mobility of charges by quasi-particle formation.
d) This makes superposition and entanglement of the collective phonon frequencies possible into a total wave function of the individual cell (i.e. the symphony of the cell) that can be holographically stored (Meijer and Geesink, 2018b).
e) The cellular oscillations are normally maintained by internal cellular energy, but, in addition, external ZP energy can also be “borrowed” in the overall process.
f) Both wave energies, in concert, seek the lowest possible energy balance in collective vibrations in all fractal parts of the cell.
g) In pure water, fractal, geometric clusters of H2O molecules are formed, each with a discrete EMF-frequency. This basic energy landscape represents the ground vibratory state of all water-containing materials.
h) The superimposed vibrations have a resonant relationship with local hydrated ions such as hydronium ions (H3O+) that can function as receivers of vibrational information. (Sbitnev, 2016). In general, inorganic ions can stabilize the coherent domains, while macromolecules together with the activated water can produce macro-coherent collective oscillation fields.
i) The underlying intra- and intercellular state of the coherent vibration domains is also influenced by quantum entanglement, which is promoted by the coherent GM frequencies. GM-scale frequencies, alone or in combination, promote the degree of entanglement, as we have demonstrated earlier (Geesink and Meijer, 2018b)
j) The cellular electrome, therefore, has a discrete internal “musical” tuning of phonons either through phonon-dressed electrons (quasi-particles such as (-) charged soliton polarons) and/or steered via freely moving hydrated protons (+) (Sbitnev, 2016)
k) The basic frequencies of all macromolecular components in the cell follow also from the known energy content of elementary wave /particles, of which the vibrations can take a rotating (spin) and longitudinal form (e.g. solitons).
l) Since all components of a cell consist of such elementary wave/particles, macromolecules also reflect related vibrations of these building blocks, as predicted by the GM-biophysical principle.
m) The entire cell content is therefore tuned by a permanent field with a dual relationship of wave frequencies selected by resonance from the quantum vacuum field oscillations and internally induced oscillations.
n) The highly facilitated movement of (+) and (–) charges in the cytoplasm may create virtual superconductive conditions in and around the cells.
o) The collective cell oscillation matrix is physically integrated by long-range connections with other parts of the organism through quantum superposition and entanglement.
p) Hexagonal water substructures enable facilitated movement of protons in the form of hydronium ions (H3O+); the latter may function as cellular electromagnetic receivers (Sbitnev, 2016).
q) This conductive aspect may also enable permanent pattern imprinting of molecular vibration in the water-layer structure and therefore may also explain the memory aspects of activated water that have been recently shown in independent reports (Montagnier et al., 2017; Magar et al., 2018, Tang et al., 2018).
r) Spectroscopic measurement of oscillation frequencies of individual proteins in aqueous solutions can, therefore, both show GM-scale coherent frequency values and decoherent values, depending on the average vibrational state of the multiple molecules dissolved. The latter may be poised between coherence/de-coherence states in a cycling mode (Vattay and Kauffman, 2015), of which the equilibrium state is also under the influence of ZPE steering.
s) Coherent wave propagation can be modeled by toroidal trajectories while decoherent wave behavior can be approached by toroidal knot theory (Meijer and Geesink, 2018a). Recently, the correspondence between solvatochromic dye reaction and biological effects of Antimonium crudum 30cH was described (Bonamin et al., 2019).
Conclusions
About 700 different frequency data have been used to define the first and second derivatives of pure water. The research resulted in 139 different first and second derivatives of spectral energy frequency curves of water molecules that can be precisely positioned at the pointer states of a calculated pattern of coherent frequencies, called the GM-scale, with an accuracy of 0.45%. Both, the imaginary parts and the real parts of the complex index of refraction (n) for liquid water can be described by this scale. The pattern has been explained and mathematically described by considering constructive quantum interference. It has been postulated that water molecules and the water molecule matrix can be considered to have a quantized character and that quantum properties such as entanglement and quantum tunneling can consequently play an important role. As pointed out in our earlier studies (Geesink and Meijer, 2018e), these wave conditions are envisioned in a fractal structure of living systems, which is much in line with the recent proposals of Turner and Nottale (2015). The molecular structure of water molecules is an open tetrahedral structure combined with a distorted tetrahedral structure (Dandekar, 2018) and fits the quantum entangled wave equation with a toroidal geometry (Amiot, 2013). The findings are clearly in line with the research of Tsenkova (aquaphotomics), in which water spectral patterns that display overtones and combined absorption bands as seen in the NIR and the mid-infrared region, are also used as a biomarker for diagnosing diseased states.
The cell and its components are always under the influence of active wave fields of internally induced EM oscillations and are at the same time driven in concert by pilot waves of the implicate order (the Broglie/Bohm concept). Recently, pilot-wave mechanisms were convincingly demonstrated in hydrodynamic experiments (Bush, 2016). Water may, therefore, also play a general role as a cosmological conduit since it is present in cosmic dust in the form of metal-doped phyllo-silicates that pervade galactic spaces in the universe. This cosmic communicating system can be modeled by toroidal geometry in a scale-invariant (holo-fractal) black hole/wormhole operator setting (Meijer and Geesink, 2017, 2018a).
We may conclude that clusters of organized water molecules in the cell provide an EMF-receptive holo-fractal network in which resonance patterns are evoked if exposed to experimental (external) EM-wave frequencies and vacuum fluctuations that are crucial for functional structure and ecology of living cells. Indeed, as put forward by Philip Ball (2017), water is an active matrix of life for cell and molecular biology, while Carniello et al. (2015) even considered a much wider perspective for water as the conduit of interactions for universal entanglement and excess correlation. In this framework, we should always realize that water, also in cells, is permanently embedded in the fluctuations of the zero point quantum vacuum field. Our studies on the relation of the GM-biological principle with entanglement promoting EM frequencies (Geesink and Meijer, 2018b), as well as our considerations on the role of water in the creation of first life and 3-D protein folding (Meijer and Geesink, 2016, 2018b; Melkikh and Meijer, 2018; Jerman 2016, 2017), are fully in line with these concepts.
Note: All of the analyzed data can be obtained directly from the first author by email request.
Discussion with Reviewers
Reviewer: Pilot Wave quantum theory, Standard Model Quantum ElectroDynamics, and String Theory, are all discussed in this article. Several phenomena are tied, either tangentially, or directly, to one of these three models. How is it that the author rationalizes these positions given that these three models are generally considered partially, if not totally, mutually exclusive?”
Authors: The main issue of our work is to stipulate that any physical system in our world is embedded in force fields that enact a guiding influence on macromolecular structures in life conditions. This steering effect can be conceived in the light of the de Broglie/Bohm pilot wave theory but also through wave resonance as assumed by quantum electrodynamics. String theory (background independent) and Loop Quantum Gravity theories (background dependent) attempt to find a basis for quantum gravity through the reconciliation of quantum field and relativity theories in attempts to picture various modes of quantum wave/particle states.
As to the claims concerning the alleged contradictions, this article testifies that there is no necessary contradiction between pilot-wave theory (Bohm) and quantum field theories (QFT) (one of them is quantum electrodynamics); on the contrary, the first may be of help to the second. And more: when one of us (Igor) was in his post-doctoral study in Great Britain, he was in intensive communication with physicists just regarding the Bohm’s (he even visited him once) theory of quantum potential. This theory (and de Broglie’s as well) is fully compatible with standard (Copenhagen) interpretation – it is rather its re-interpretation. And the standard quantum theory is fully compatible with quantum electrodynamics. Therefore, there should be no fundamental contradiction, nor a true exclusiveness.
Regarding the supposed exclusiveness between the QFT and String theory: the latter (actually some five of them) represents a trial on how to reconcile the quantum field theory (or quantum mechanics) with Einstein’s relativity theory. No success as yet, but this very effort of reconciliation proves that, in principle, there is common ground for QFT and the String theories. String theory and Loop Quantum theory are even more related than is generally assumed. https://www.quantamagazine.org/string-theory-meets-loop-quantum-gravity-20160112/. In conclusion: our wave guiding modality can be expressed in various interpretations of QM as well as basic models for the fabric of quantized reality: they all clearly touch upon field-dependent mechanisms involved in the creation of life.
References
Amiot E, 2013. The Torii of Phases. In: Yust J., Wild J., Burgoyne JA(eds) Mathematics and Computation in Music. MCM 2013. Lecture Notes in Computer Science, 7937. Springer, Berlin, Heidelberg.
Arani R, Bono I, Giudice ED, Preparata G, 1995. QED coherence and the thermodynamics of water. Journal of Modern Physics B. 9: 1813-1842.
Baldassarre M, Chenge L, Eremina N, Goormaghtig E, Barth A, 2010. Simultaneous Fitting of Absorption Spectra and Their Second Derivatives for an Improved Analysis of Protein Infrared Spectra. Bass M. Handbook of Optics: Volume IV – Optical Properties of Materials, Nonlinear Optics, Quantum Optics, Third Edition.
Ball P, 2017. Water is an active matrix of life for cell and molecular biology, PNAS, 114 (51): 13327-13335; https://www.pnas.org/content/114/51/13327.
Bazar G., Kovacs Z., and Tsenkova R, 2016. Evaluating spectral signals to identify spectral error. PLoS ONE 11: e0146249.
Bechhoefer J, Ego V, Manneville S, Johnson B, 1995. An experimental study of the onset of parametrically pumped surface waves in viscous fluids. J. Fluid Mech. 288: 325–350.
Bellissent-Funel M C et al., 2016. Water Determines the Structure and Dynamics of Proteins. Chem. Rev., 116 (13), pp 7673–7697, May 17, 2016.
Bloino J, Biczysko M, Barone V, 2015. Anharmonic Effects on Vibrational Spectra Intensities: Infrared, Raman, Vibrational Circular Dichroism and Raman Optical Activity. J Phys Chem A. 119(49): 11862–11874.
Bohm D, 1952. A Suggested Interpretation of the Quantum Theory in Terms of “Hidden” Variables, I & II. Physical Review, 85, 166-179.
Bonamin L V, et al., 2019. Characterization of Antimonium crudum Activity Using Solvatochromic Dyes. Homeopathy.
Bono I, Del Giudice E, Gamberale L, Henry M, 2012. Emergence of the Coherent Structure of Liquid Water, Water, 4(3), 510-532.
Braun C H, Smirnov S N, 1993. Why is water blue? J Chem Edu 70: 612–614.
Buiteveld H J, Hakvoort H M, Donze M, 1994. The optical properties of pure water,” in Ocean Optics XII, Jaffe J S ed., Proc. SPIE 2258: 174–183.
Burns D A, Ciurczak E W, 2007. Handbook of Near-Infrared Analysis. CRC Press. ISBN 9780849373930 – CAT# 7393.
Busarow K L, Cohen R C, Blake G A, Laughlin K B, Lee Y T, Saykally R J, 1989. Measurement of the Perpendicular Rotation-Tunneling Spectrum of the Water Dimer by Tunable Far Infrared Laser Spectroscopy in a Planar Supersonic Jet. J Chem Phys 90(8):3937–3943.
Bush J W M, 2015. Pilot wave Hydrodynamcs. Annu. Rev. Fluid Mech. 47: 26992.
Carniello T N, Vares D A E, Persinger M A, 2015. Quantitative Support for Water as the Conduit of Interaction for Universal Entanglement. Journal of Consciousness Exploration & Research 6 (9): 738-749.
Chai B-H, Zheng J-M, Zhao, Pollack G H, 2008. Spectroscopic studies of solutes in aqueous solution. J. Phys. Chem. A 112: 2242–2247.
Chaplin M, 2006. Do we underestimate the importance of water in cell biology? Nat. Rev. Mol. Cell Biol. 7 (11): 861–6.
Chaplin M. 2007. Water’s Hydrogen Bond Strength, arXiv:0706.1355 [cond-mat.soft].
Chladni E F F, 1980. Entdeckungen über die Theorie des Klanges [Discoveries in the Theory of Sound], Leipzig, 1787; pp. 78; Reprint, Leipzig.
Clegg J, 2018. Properties and metabolism of the aqueous cytoplasm and its boundaries. Downloaded from www.physiology.org/journal/ajpregu (084.031.212.213).
Colleonia C et al., 2014. Delayed luminescence induced by complex domains in water and in aqueous solutions. arXiv:1411.2221v1 [physics.chem-ph].
Dandekar R, Hassanali A A, 2018. Hierarchical Lattice Models of Hydrogen Bond Networks in Water. arXiv:1709.08703v2 [cond-mat.stat-mech].
Davies A M C, 2005. An Introduction to near Infrared Spectroscopy.
De Loof, A., 2016. The cell’s self-generated “electrome”: The biophysical essence of the immaterial dimension of Life?. Communicative & integrative biology, 9(5), p.e1197446.
De Ninno A, Castellano A C, Del Giudice E, 2013. The supramolecular structure of liquid water and quantum coherent processes in biology. Journal of Physics: Conference Series 442: 012031.
Del Giudice E, De Ninno A, Fleischmann M, Mengoli G, Milani M, Talpo G, Vitiello G, 2005. Coherent quantum electrodynamics in living matter. Electromagnetic Biology & Medicine 24: 199-210.
Del Giudice E, Preparata G, 1998. Electrodynamical Like-Charge Attractions in Metastable Colloidal Crystallites, Modern Physics Letters B 12: 881-886.
Del Giudice E, Tedeschi A, 2009. Water and Autocatalysis in Living Matter, Electromagnetic Biology and Medicine, 28: 46–52.
Del Giudice E, Spinetti P R, Tedeschi A, 2010. Water dynamics at the root of metamorphosis in living organisms. Water 2: 566–586.
Del Giudice E, Vitiello G, 2011. Influence of Gravity on the Collective Molecular Dynamics of Liquid Water: The Case of the Floating Water Bridge, Water, 2: 133-141.
Du L, Mackeprang K, Kjaergaard H G, 2013. Fundamental and overtone vibrational spectroscopy, enthalpy of hydrogen bond formation and equilibrium constant determination of the methanol–dimethylamine complex, Phys. Chem. Chem. Phys., 15 :10194-10206.
Dunn M E, Timothy M E, Kirschner K N, Shields G C, 2006. Prediction of Accurate Anharmonic Experimental Vibrational Frequencies for Water Clusters, (H2O)n, n=2-5. Phys Chem A. 110(1): 303–309.
Faraday M, 1831. On a Peculiar Class of Acoustical Figures; and on Certain Forms Assumed by Groups of Particles upon Vibrating Elastic Surfaces. Proc. R.Soc. 121: 299–340.
Flores-Livas J A et al., 2017. Emergence of superconductivity in doped H2O ice at high pressure, Scientific Reports 7: 6825.
Fröhlich H, 1968. Long-range coherence and energy storage in biological systems. Int. J. Quantum Chem. 2: 641–649.
Fröhlich H, 1978. Coherent Electric Vibrations in Biological Systems and the Cancer Problem. IEEE Transactions on Microwave Theory and Techniques 26(8): 613-617.
Fröhlich H, 1988. Theoretical physics and biology, in Biological Coherence and Response to Extemal Stimuli, Frohlich H ed., Springer Verlag, Berlin, 1-24.
Ganeshan S, Ramírez R, Fernández-Serra M V, 2013. Simulation of quantum zero-point effects in water using a frequency-dependent thermostat, Phys. Rev. B 87, 134207.
Geesink J H, Meijer D K F, 2016. Quantum Wave Information of Life Revealed: An Algorithm for Electromagnetic Frequencies that Create Stability of Biological Order, with Implications for Brain Function and Consciousness. NeuroQuantology 14: 106-125.
Geesink J H, Meijer D K F, 2017a. Bio-Soliton Model that Predicts Non-Thermal Electromagnetic Frequency Bands, that Either Stabilize Living Cells. Electromagnetic Biology and Medicine 36: 357-378.
Geesink J H, Meijer D K F, 2017b. Electromagnetic Frequency Patterns that are Crucial for Health and Disease Reveal a Generalized Biophysical Principle: the GM scale. Quantum Biosystems 8: 1-16.
Geesink J H, Meijer D K F, 2018a. Semi-Harmonic Scaling enables Calculation of Masses of Elementary Particles of the Standard Model. J Modern Physics 9(5): 925-947. doi.org/10.4236/jmp.2018.95057.
Geesink J H, Meijer D K F, 2018b. Mathematical Structure of the GM Life Algorithm that May Reflect Bohm’s Implicate Order. J. Modern Physics 9: 851- 897.
Geesink J H, Meijer D.K F, 2018c. A semi-harmonic electromagnetic frequency pattern organizes non-local states and quantum entanglement in both EPR studies and life systems. J. Modern Physics 9: 898-924.
Geesink J H, Meijer D.K F, 2018d. Evidence for a Guiding Coherence Principle in Quantum Physics, Quantum Biosystems 9(1): 1- 7.
Geesink J H, Meijer D.K F, 2018e. A novel biophysical quantum algorithm, predicts superconductive properties in animate and inanimate systems, submitted to Quantum Biosystems.
Gorshunov B P et al., 2013. “Quantum Behavior of Water Molecules Confined to Nanocavities in Gemstones,” J. Phys. Chem. Lett. 4 (12), 2015-2020.
Groenenboom G C et al., 2000. Water pair potential of near spectroscopic accuracy. II. Vibration–rotation–tunneling levels of the water dimer. The Journal of Chemical Physics, 113(16): 6702-6715.
Hale G M, Querry M R, 1973. Optical Constants of Water in the 200-nm to 200-Mm Wavelength Region, Appl. Opt. 12: 555.
Heller J M et al., 1974. Collective Oscillation in Liquid Water. J. Chem. Phys., 60: 3483-3486.
Henry M, 2016. Hofmeister Series: The Quantum Mechanical Viewpoint. Current Opinion in Colloid & Interface Science; 23, 119-125.
Heßelmann A, 2018. Correlation effects and many-body interactions in water clusters. Beilstein J. Org. Chem. 14: 979–991.
Mae-Wan H, 2015. Illuminating water and life: Emilio Del Giudice. Electromagn. Biol Med 34(2): 113-122.
Hodges M P, Stone A J, Xantheas S S, 1997. J. Phys. Chem. A, 101: 9163.
Iwamoto M, Uozumi J, Nishinari K, 1987. “Preliminary investigation of the state of water in foods by near infrared spectroscopy,” in Proceedings of the International NIR/NIT Conference. eds J. Hollo, K.J. Kafka and J. Gonzcy (Budapest: Akademiai Kiado).
Jerman I, 2016. The Origin of Life from Quantum Vacuum, Water and Polar Molecules. American Journal of Modern Physics;5(4-1):34-43.
Jerman I, 2017. What Nanobacteria and Nanovesicles May Tell Us about the Origin of Life? Open Access Library Journal, 4(01): e3348.
Jinendra B, 2011. Near Infrared Spectroscopy and Aquaphotomics: Novel Tool for Biotic and Abiotic Stress Diagnosis of Soybean. Kobe: Kobe University.
Kajander E, 2006. Nanobacteria – propagating calcifying nanoparticles. Lett. Appl. Microbiol., 42 (6): 549-552.
Karlberg J B, Pacey C E, 1989. Flow Injection Analysis. A Practical Guide, Elsevier, Amsterdam.
Keutsch F N, Saykally R J, 2001. Water clusters: Untangling the mysteries of the liquid, one molecule at a time, PNAS 98(19): 10533-10540.
Kinoshita K et al., 2012. Spectral pattern of urinary water as a biomarker of estrus in the giant panda. Scientific Reports 2: 856.
Kovacs Z. et al., 2015. Monitoring of Water Spectral Pattern Reveals Differences in Probiotics Growth When Used for Rapid Bacteria Selection. PLOS ONE.
Kühne T D, Khaliullin R Z, 2013. Electronic signature of the instantaneous asymmetry in the first coordination shell of liquid water. Nature Communications 4: 1450.
Litjens R A J, Quickenden T I, Freeman C G, 1999. Visible and near-ultraviolet absorption spectrum of liquid water, Applied Optics 38(7): 1216-1223.
Liu Y et al., 2017. Molecular couplings and energy exchange between DNA and water mapped by femtosecond infrared spectroscopy of backbone vibrations, Structural Dynamics 4: 044015.
Lobyshev V I, Shikhlinskaya R E, Ryzhikov B D, 1999. Experimental evidence for intrinsic luminescence of water. J. Mol. Liq. 82: 73–81.
Magar S et al., 2018. Ultra-diluted Toxicodendron pubescens attenuates pro-inflammatory cytokines and ROS- mediated neuropathic pain in rats. Nature Scientific Reports 8:13562. (retracted).
Maheshwary S., Patel N., Sathyamurthy N, Kulkarni A D, Gadre S R, 2001. Structure and Stability of Water Clusters (H2O)n, n = 8 – 20: An ab initio Investigation. The Journal of Physical Chemistry 105: 10525-10537.
Martel et al., 2014. Of Nanobacteria, Nanoparticles, Biofilms and Their Role in Health and Disease: Facts, Fancy and Future. Nanomedicine, 9: 483-499.
Mason J D, Cone M T, Fry S F, 2016. Ultraviolet (250–550 nm) absorption spectrum of pure water. Applied optics 55(25): 7163-7172.
Matsuhiro B, Rivas P, 1993. Second-derivative Fourier transform infrared spectra of seaweed galactans. Journal of Applied Phycology 5: 45-51.
Matthews D A, Vázquez J, Stanton J F, 2007. Calculated stretching overtone levels and Darling–Dennison resonances in water: a triumph of simple theoretical approaches. Molecular Physics 105: 19-22 .
Mc Dermott M Let al., 2017. DNA’s Chiral Spine of Hydration. ACS Central Science 3: 708-714.
Meijer D K F, Geesink J H, 2016. Phonon Guided Biology. Architecture of Life and Conscious Perception are mediated by Toroidal Coupling of Phonon, Photon and Electron Information Fluxes at Discrete Eigenfrequencies. NeuroQuantology 14(4): 718-755.
Meijer D K F, Geesink J H, 2017. Consciousness in the Universe is Scale Invariant and Implies the Event Horizon of the Human Brain. NeuroQuantology 15(1): 41-79.
Meijer D K F, Geesink J H 2018a. Is the Fabric of Reality Guided by a Semi-Harmonic, Toroidal Background Field? International Journal of Structural and Computational Biology, Symbiosis.
Meijer D K F, Geesink J H, 2018b. Guided folding of life’s proteins in integrate cells with holographic memory and GM-biophysical steering. Open Journal Of Biophysics 8(3):117-154.
Melkikh A V, Meijer D K F, 2018 . On a generalized Levinthal’s paradox: the role of long- and short range interactions on complex bio-molecular reactions, including protein and DNA folding. Progress in Biophysics and Molecular Biology 132: 57-79.
Miroslaw J, 2007. Absorption coefficient of water. Data sources: www.tpdsci.com/Tpc/AbsCfOfWaterDat.php, data of Pope RM and Fry 1997 and of Kou L et al. 1993. In: Top. Part. Disp. Sci. (www.tpdsci.com). ISBN 978-0-9780628-0-4.
Mitchell E D, Staretz R, 2011. The Quantum Hologram and the Nature of Consciousness. Journal of Cosmology 14: 1-35.
Montagnier L et al., 2015. Transduction of DNA Information through Water and Electromagnetic Waves. Electromagnetic Biology and Medicine , 34, 106-112.
Montagnier L et al., 2017. Water Bridging Dynamics of Polymerase Chain Reaction in the Gauge Theory Paradigm of Quantum Fields. Water 9(6) 339.
Morel A., 1974. Optical properties of pure water and pure seawater. In: Optical Aspects of Oceanography, Jerlov N. G., and Steeman, E. eds. (Academic, 1974), pp. 1–24.
Pasquini C J, Braz. 2003. Near Infrared Spectroscopy: Fundamentals, Practical Aspects and Analytical Applications. Chem. Soc. 14(2): 198-219.
Pegau W S, Gray D, Zaneveld J R V, 1997. Absorption and attenuation of visible and near-infrared light in water: dependence on temperature and salinity, Applied Optics 36(24): 6035-6046.
Persson E, Halle B, 2008. Cell water dynamics on multiple time scales. Proc. Natl. Acad. Sci. 105(17): 6266–71. PMC 2359779. PMID 18436650.
Plankar M, Del Giudice E, Tedeschi A, Jerman I, 2012. The role of coherence in a systems view of cancer development, Theoretical Biology Forum, 105(2): 15 – 46. PMID: 23757952.
Pope R M, Fry E S, 1997. Absorption spectrum ~380–700 nm of pure water. II. Integrating cavity measurements 36(33): 8710-8723.
Pollack G H, 2013. The fourth phase of water: beyond solid, liquid, and vapor. Ebner and Sons Publishers: Seattle.
Preparata G., QED Coherence in matter, Singapore: World Scientific, 1995.
Pugliano N, Saykally RJ, 1992. Measurement of quantum tunneling between chiral isomers of the cyclic water trimer, Science 257(5078): 1937-1940.
Pugliano N, 1992. Vibration-Rotation-Tunneling Dynamics in Small Water Clusters. PhD Thesis.
Rayleigh L, 1883. VII. On the crispations of fluid resting upon a vibrating support. Philosophical Magazine Series 5(16): 50–58.
Querry M R, Cary P G, and Waring R C, 1978. Split-Pulse Laser Method for Measuring Attenuation Coefficients of Transparent Liquids: Application to Deionized Filtered Water in the Visible Region Appl. Opt. 17: 3587.
Richardson J O et al., 2016. Concerted hydrogen-bond breaking by quantum tunneling in the water hexamer prism. Science 351(6279): 1310–1313.
Ritz W, 1909. Theorie der Transversalschwingungen einer quadratischen Platte mit freien Rändern. Annalen der Physik 333(4): 737-786.
Sahu S, Ghosh S, Ghosh B, Aswani K, Hirata , Fujita D, Bandyopadhyay A , 2013. Atomic water channel controlling remarkable properties of a single brain microtubule: Correlating single protein to its supramolecular assembly. Biosensors and Bioelectronics 47(2013): 141–148.
Sbitnev V I, 2016. Quantum Consciousness in Warm, Wet, and Noisy Brain. Modern Physics Letters B. 30(28): 1650329.
Scholes G D, 2010. Quantum-coherent electronic energy transfer: Did Nature think of it first? The Journal of Physical Chemistry Letters, 1(1): 2-8.
Segelstein J, 1981. The complex refractive index of water. Department of Physics. University of Missouri-Kansas City, 1981.
Sen S, Gupta K S, Coey J M D, 2015. Mesoscopic structure formation in condensed matter due to vacuum fluctuations, PHYSICAL REVIEW B 92, 155115.
Sheldrake M, Sheldrake R, 2017. Determinants of Faraday Wave-Patterns in Water Samples Oscillated Vertically at a Range of Frequencies from 50-200 Hz, Water Journal 9: 1-27.
Shiraga K, Ogawa Y, Kondo N, 2016. Hydrogen Bond Network of Water around Protein Investigated with Terahertz and Infrared Spectroscopy. Jane Dyson Biophysical Journal 111: 2629–2641.
Smith R C, Baker K S, 1981. Optical properties of the clearest natural waters (200-800 nm). Applied Optics 20(2): 177-184.
Stomp M, Huisman J, Stal L J, Matthijs H C P, 2007. Colorful niches of phototrophic microorganisms shaped by vibrations of the water molecule. The ISME Journal, 1(4): 271–282.
Sogandares F M, 1991. The spectral absorption of pure water. Ph.D. dissertation. Texas A&M University, College Station, Tex.
Sogandares F M, Fry E S, 1997. Absorption spectrum (340–640 nm) of pure water. I. Photothermal measurements. Applied Optic 33: 8699–8709.
Tam A C, Patel C K N, 1979. Optical absorptions of light and heavy water by laser optoacoustic spectroscopy. Applied Optic 18, 3348–3358.
Tang, B.Q., Li, T., Bai, X., Zhao, M., Wang, B., Rein, G., Yang, Y., Gao, P., Zhang, X., Zhao, Y. and Feng, Q., 2019. Rate limiting factors for DNA transduction induced by weak electromagnetic field. Electromagnetic biology and medicine, 38(1): 55-65.
Thar R, Kühl M, 2004. Propagation of electromagnetic radiation in mitochondria? J. Theoretical Biology, 230: 261-270.
Tielrooij K J, Timmer R L A, Bakker H J, Bonn M, 2009. Structure Dynamics of the Proton in Liquid Water Probed with Terahertz Time-Domain Spectroscopy. Phys. Rev. Lett., 102:198303.
Tsenkova R, Atanassova S, Itoh K, Ozaki Y, Toyoda K, 2000. Near infrared spectroscopy for biomonitoring: cow milk composition measurement in a spectral region from 1,100 to 2,400 nanometers. J Anim Sci. 78:515-522.
Tsenkova R N, Iordanova I K, Toyoda K, Brown D R, 2004. Prion protein fate governed by metal binding. Biochemical and biophysical research communications, 325(3): 1005-1012.
Tsenkova R, 2007. AquaPhotomics: water absorbance pattern as a biological marker for disease diagnosis and disease understanding. NIR News. 18(2): 14-16.
Tsenkova R, Muncan J, Pollner B, Kovacs Z, 2018. Essentials of Aquaphotomics and Its Chemometrics Approaches. Frontiers in Chemistry Frontiers in chemistry 6: 363.
Turner P, Nottale L, 2015. The origins of macroscopic quantum coherence in high temperature superconductivity. Physica C: Superconductivity and its Applications 515: 15-30.
Turner P, Nottale L, 2017. The physical principles underpinning self-organization in plants. Progress in biophysics and molecular biology 123: 48-73.
Vitiello G, 2001. My double unveiled: the dissipative quantum model of brain. Amsterdam: John Benjamins.
Vitiello G, 2009. Coherent states, fractals and brain waves, New Mathematics and Natural Computation (NMNC), 5: 245-264.
Vattay G, Salahub D, Csabai I, Nassimi A, Kaufmann S A, 2015. Quantum criticality at the origin of life. In Journal of Physics: Conference Series 626(1): 012023.
Wang L, 2008. Measuring optical absorption coefficient of pure water in UV using the integrating cavity absorption meter. Ph. D. thesis. Texas A&M University.
Wieliczka D M, Weng S, Querry M R, 1989. Wedge shaped cell for highly absorbent liquids: infrared optical constants of water. Appl. Opt. 28: 1714-1719.
Wiggins P M, 1996. High and low density water and resting, active and transformed cells. Cell Biol. Int. 20(6): 429–35. PMID 8963257.
Wozniak D, Jerzy B, 2007. Light Absorption in Sea Water. Book ISBN 978-0-387-49560-6.
Wu C-Y et al., 2013. Bions: A Family of Biomimetic Mineralo-Organic Complexes Derived from Biological Fluids. PloS ONE 8: e75501.
Yaghobee S et al., 2015. What Are the Nanobacteria? Biotechnology & Biotechnological Equipment 29: 826-833.
Yang S-Y et al., 2014. NIR spectroscopic analysis for wood water molecules. Wood and Fiber Science 46(2): 138-147.
Yasui T, Araki T, 2011. Sensitive measurement of water content in dry material using low-frequency terahertz time-domain spectroscopy system equipped with micro-structured photoconductive antennas, 1st EOS Topical Meetingon Micro- and Nano-Optoelectronic Systems. European Optical Society. Bremen, Germany. ISBN 978-3-00-033711-6.
Ying-Ya Liu, Yi-Lun Ying, Xin Hua, Yi-Tao Long, In-situ discrimination of the water cluster size distribution in aqueous solution by ToF-SIMS. Science China Chemistry February 2018, Volume 61, Issue 2, pp 159–163.
Young J D, Martel J, 2010. The Rise and Fall of Nanobacteria, Scientific American 302(1): 52-59.
Zhao Q, Zheng J, Chai B, Pollack G H, 2008. Unexpected effect of light on colloidal crystal spacing. Langmuir 24: 1750–1755.
Zavadlav J, Siewert J M, Praprotnik M, 2018. Multiscale Simulation of Protein Hydration Using the SWINGER Dynamical Clustering Algorithm. J. Chem. Theory Comput. 14: 1754-1761.
Zheng J M, Chin W-C, Khijniak E, Khijniak E Jr, Pollack G H, 2006. Surfaces and interfacial water: Evidence that hydrophilic surfaces have long-range impact. Advances in Colloid and Interface Science 127: 19–27.
Zheng J M, Wexler A, Pollack G H, 2009. Effect of buffers on aqueous solute-exclusion zones around ion-exchange resins. Journal of Colloid and Interface Science 332: 511–514.
Zurek W H, 1998. Decoherence, einselection and the existential interpretation (the rough guide). Philosophical Transactions of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences 356(1743): 1793-1821.
Zheng J-M, Pollack G H, 2003. Long-range forces extending from polymer-gel surfaces. Phys. Rev. E 68: 031408.
Appendices
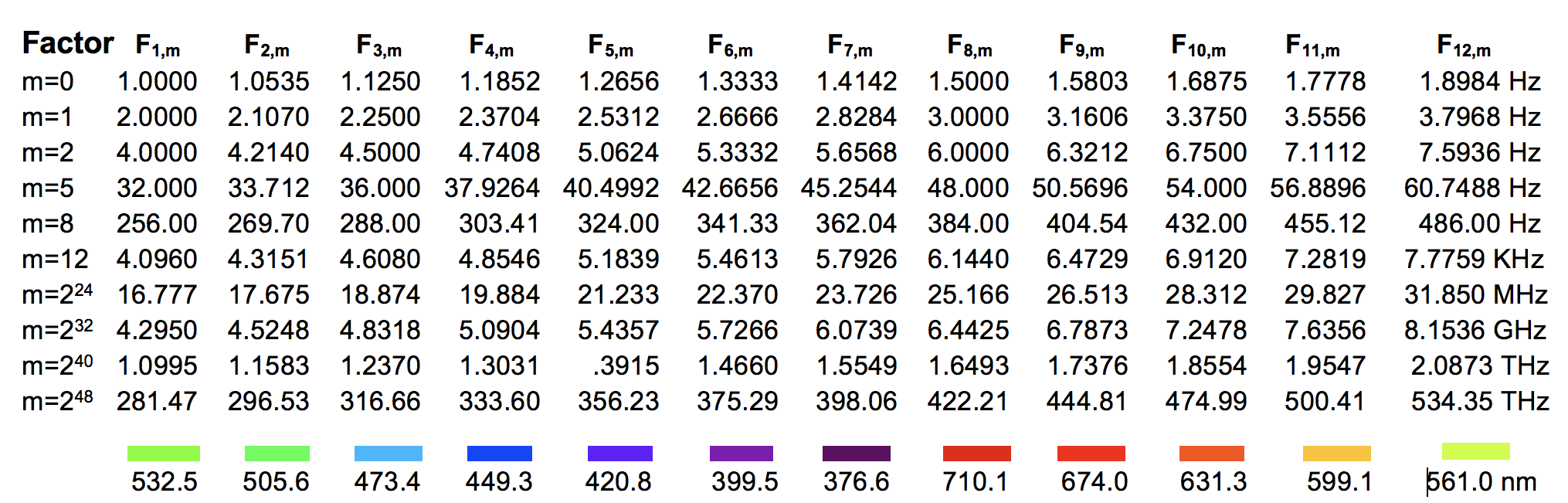
Appendix 1: GM-scale: calculated examples of coherent frequencies from sub Hertz to PHz.
Appendix 2: The different analyzed pure water spectra
All of the analyzed data can be obtained directly from the first author by email request.
Appendix 3: First and second derivatives (nm and µm) derived from the different graphs for pure water
nm: 105.97, 105.43, 111.30, 112.7, 119.21, 126.26, 133.32, 140.41, 149.38, 149.46, 156.94, 280, 300, 315, 335, 348, 377, 316, 337, 355, 377, 399.5, 399, 403, 417, 419, 420, 420, 449, 450, 449.2, 450, 472, 475, 476, 504, 505, 505, 508, 510, 532, 533, 533, 561, 561, 561.3, 597, 598, 600, 600.5 629, 630, 640.0, 670.7, 672.0, 673, 675, 705.0, 712, 750.0, 752, 800, 805.0, 850.0, 855.0, 900.0, 912.5, 950.0, 966.0, 1000, 1020.0, 1050.0, 1062.,5 1105.0, 1105, 1195, 1270, 1350, 1420, 1505, 1600, 1695, 1805, 1900, 2020, 2135, 2240, 2380.
µm: 0.75, 0.799, 0.84, 0.90, 0.95, 1.01, 1.08, 1.12, 1.19, 1.25, 1.35, 1.26, 1.36, 1.41, 1.42, 1.50, 1.52, 1.58, 1.60, 1.68, 1.68, 1.80, 1.80, 1.90, 1.94, 2.02, 2.05, 2.13, 2.14, 2.30, 2.40, 2.43, 2.50, 2.52, 2.65, 2.70, 2.82, 2.99, 2.99, 3.15, 3.40, 3.60, 3.80, 4.05, 4.30, 4.80, 5.01, 5.40, 5.70, 6.10, 6.40, 6.70, 7.20 , 7.50, 9.00, 11.0, 12.0, 4408.7, 4163.78, 3858.33, 3656.00, 3406.73, 3258.61, 3074.79, 2939.14, 2725.38, 2562.33, 2477.62, 2306.10.
Appendix 4: All of the calculated data can be obtained directly from the first author by email request.
Appendix 5: All of the calculated data can be obtained directly from the first author by email request.
