A New Hydrogen Bond Angle/Distance Potential Energy Surface of the Quantum Water Dimer

A New Hydrogen Bond Angle/Distance Potential Energy Surface of the Quantum Water Dimer

Scott, JN¹; Vanderkooi, JM^2,*

¹ Department of B Department of Biochemistry and Biophysics, School of Medicine, University of Pennsylvania, 257 Anatomy-Chemistry Bldg., 3620 Hamilton Walk, Philadelphia, PA 19104, USA

^* Correspondence: Tel.: (215)898-8783, Fax: (215)573-2085; Email: [email protected]

Key Words: water dimer, potential energy surface, hydrogen bonds, water structure, quantum dimer, hydrogen bond angle

Received September 2, 2009; accepted January 8, 2010. Published February 5, 2010; available online February 5, 2010

doi: 10.14294/WATER.2010.1

Summary

The relative effects of H-bond angle and O-O distance were examined using a series of quantum mechanical calculations on a water dimer. The geometries were constructed in such a way that H-bond angle and O-O separation were the only two independent variables, and this allowed for calculations of energies and atomic charges as a function of H-bond angle and O-O distance. Our findings show that O-O separation within the range 0.25 nm to 0.40 nm has a lesser effect on system energy and charge as compared to changes in H-bond angle, and that energy as a function of O-O separation behaves very much like a Morse potential for linear H-bonds but not for bent hydrogen bonds. Recent literature in the water dimer field is discussed, as is the application of the current findings to bulk water.

Article Outline

• Introduction
• Materials and Methods
• Results
• O-O Energy
• Fits Charges
• Discussion
• Conclusions
• References
• Discussion With Reviewers

Introduction

The H-bond is one of the most fundamental interactions in chemistry, and the role of H-bonds in the formation of liquid water is the context in which they have most often been studied. From the very early qualitative descriptions of water H-bonds by Latimer and Rodebush (1920) to the recent highly detailed multidimensional water dimer and trimer potential energy surfaces calculated at high levels of quantum theory by Huang et al. (2008) and Wang et al. (2008), water H-bonding continues to be an extremely active area of research with many researchers attempting to better understand the H-bond both qualitatively and quantitatively.

H-bonding is found not only in water but also in a wide range of biologically interesting molecules. When contemplated within the framework of modern biochemistry H-bonds take on a new role. Beyond a mere theoretical curiosity, H-bonds have been shown to be critical determinants of biomolecular structure and function (Creighton, 1991, Levy and Onuchic, 2006, Oleinikova et al. 2005, Riley and Hobza, 2007, Vanderkooi et al. 2005). Indeed, even intermolecular water H-bonding itself has been increasingly implicated in direct and indirect roles it may have on biologically relevant molecules (Dashnau et al. 2006, Dashnau et al. 2008, Levy and Onuchic, 2006, Nucci and Vanderkooi, 2005, Scott et al. 2008, Sharp et al. 2001, Sharp and Vanderkooi, 2009, Sorin et al. 2006, Vanderkooi et al. 2005).

Though there is widespread agreement that H-bonding is very important, both in its theoretical context and for its effect on the elements of life, there is still no consensus as to the precise nature of the H-bond or exactly what constitutes an H-bond (Barbiellini and Shukla, 2002, Gallagher and Sharp, 2003, Isaacs et al. 1999, Isaacs et al. 2000, Kumar et al. 2007, Smith et al. 2004, Weinhold et al. 2005, Wernet et al. 2004). Insofar as water is concerned, the principle problem lies in the fact that there exists no experimental probe of water-water orientation. Therefore, though radial distribution functions can be obtained for bulk water’s individual atoms using scattering methods (Brady et al. 2006, Hura et al. 2000, Narten and Levy, 1971, Soper, 2000, Soper and Phillips, 1986, Strassle et al. 2006, Wernet et al. 2004), it is difficult to determine with any degree of experimental certainty the average intermolecular geometry of condensed phase water molecules.

Fortunately where direct experimental evidence is lacking theoretical methods still allow us to probe chemically interesting systems or interactions. The water dimer is one such system, constituting the simplest example of a water-water H-bond. This system is especially amenable to study using quantum mechanical methods due to its relatively small number of electrons. The water dimer has even become a de facto test for new quantum mechanical methods since there is experimental gas phase binding data against which their results can be compared (Curtiss et al. 1979, Mas et al. 2000).

A great deal of the quantum mechanical work on the water dimer has aimed at describing local minima and stationary points in its multidimensional potential energy surface (see Ref. (Scheiner, 1994) for an excellent review of early work in the field). A recent study by Shank et al. (2009), for instance, fits a coupled cluster calculated 30,000 point full-dimensional global PES, encompassing 10 stationary points, for a water dimer. The present study differs from this and other previous studies of the water dimer PES in that we chose to not only simplify the two water monomers by fixing their internal geometries but that we also purposefully restricted the intermolecular orientation to examine very specific variables. As such, the vast majority of our calculated PES is far away from any sort of minimum structure or transition state. Our reasoning for adopting this approach was twofold. Since the dimer is used as a simplified mock up of liquid water, and liquid water itself contains constantly fluctuating H-bonds, we reasoned that areas of the PES far away from equilibrium might be of interest in their applicability to H-bond geometries in real water. This simplified approach also gave us the opportunity to specifically address the relative, independent effects of H-bond angle and H-bond length, which in this case were defined as the HOO angle and the O-O distance.

Materials and Methods

The internal molecular geometry for each water molecule constituting the water dimers studied was constructed such that its OH lengths were set to 0.0991 nm and its HOH angle was set to 105.5° (Silvestrelli and Parrinello, 1999). This internal geometry was held rigid for both water monomers throughout all of the calculations described here. The dimers were then formed to test two general hydrogen bonding schemes. In the first formulation, the H-bond donor molecule’s oxygen atom and the H-bond donor hydrogen were placed in the plane with the H-bond acceptor water molecule (Figure 1A). This geometry is henceforth referred to as “planar” for the sake of brevity. In the second H-bonding arrangement, the H-bond donor molecule is placed relative to the H-bond acceptor molecule such that it donates its H-bond to lone pair electrons of the H-bond acceptor’s oxygen atom (Figure 1B) (Odutola and Dyke, 1980). This geometry will hereafter be referred to as “tetrahedral.”

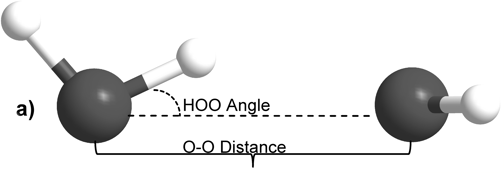
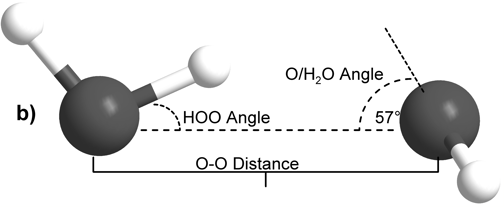
Figure 1: Intra- and inter-molecular geometries of the “planar” and “tetrahedral” water dimers.

All calculations were carried out using Gaussian 03 Revision D.01 (Frisch, 2004). All data manipulation and plotting was performed using MATLAB 7.6.0. Calculations for each geometry were performed using both MP2 (Head-Gordon et al. 1988) and B3LYP (Becke, 1993, Lee et al. 1988, Miehlich et al. 1989) chemistries with the aug-cc-pVTZ (Davidson, 1996, Kendall et al. 1992) and 6-311++G(d,p) (Krishnan et al. 1980) basis sets respectively. These chemistry/basis set combinations are not sufficient for high level calculations of H-bond interactions (Boese et al. 2007, Bukowski et al. 2008, Inada and Orita, 2007, Lee, 2007, Riley and Hobza, 2007, Santra et al. 2007, Schutz et al. 1997) (the coupled cluster methods currently give the most accurate H-bonding energies (Huang et al. 2008, Shank et al. 2009, Tschumper et al. 2002)) but were deemed to be acceptable for the sort of comparative analysis performed in this study. All vacuum energy calculations used the counterpoise method of basis set superposition error correction (Boys and Bernardi, 1970, Simon et al. 1996).

In addition to standard gas phase vacuum calculations, the Polarizable Continuum Model (PCM) solvation model (Cossi et al. 2003) was also implemented in an effort to place the H-bonded dimer in the context of a simple liquid water reaction field. The PCM solvation method is rudimentary when compared with the effect of explicit first solvation shell water molecules, but the inclusion of first shell water molecules would have made it difficult, if not impossible, to unambiguously attribute changes in the PES to intermolecular orientation of the H-bond of interest. The combinations of dimer geometry, model chemistry and basis set, and solvation state yielded eight complete data sets. All figures shown in this paper are for the cases of the planar and tetrahedral water dimers in vacuum, calculated using the MP2/aug-cc-pVTZ model chemistry and basis set. Data for the other six combinations of dimer geometry, model chemistry and basis set, and solvation state is discussed in the text, however, figures for these combinations have not been included, since the two cases for which figures have been shown were felt to be representative and sufficient.

For both H-bonding dimer geometries, the O-O distance was scanned at a fixed H-bond angle, defined herein as the angle between the H-bond donor molecule’s donor OH vector and the O-O vector. The H-bond angle was subsequently increased by one degree and the O-O distance was scanned again for the new angle. Angles from 0° to 90° in 1° increments were used, and O-O distances from 0.25 nm to 0.40 nm were scanned at every 0.01 nm. For each O-O distance and HOO angle system energy was calculated. Natural Population Analysis, a part of the Natural Bond Orbital formalism (Rives and Weinhold, 1980), was used to calculate atomic charges. The calculated energy surface for the dimers was also examined by taking slices along the H-bond angle dimension. This subset of the data was analyzed by fitting the energy vs. O-O distance data for a particular H-bond angle to the Morse potential function,

[1] V(r)= D_e (1 – e^-a(r-re))²

Results

Energies: Energies are given in kcal/mol, relative to the calculated minimum energy for a particular set of calculations. The true calculated minimum energy and O-O distance/H-bond angle position of that energy for each of the eight sets of calculations is given in Table I. In Figures 2A and 3A the 3-dimensional energy landscapes for the MP2/aug-cc-pVTZ planar and tetrahedral vacuum cases are shown and Figures 2B and 3B contain the same information in 2-dimensional color mapped projections. Each of the calculated energy surfaces has the same essential characteristics, indicating that the trends we observe are not simply model or basis set dependent. Each of the surfaces has its global minimum at an H-bond angle of about 0° (the angle is somewhat distorted for both of the tetrahedral vacuum cases) and an O-O distance of about 0.29 nm. Increases in O-O distance beyond the global minimum for a given PES result in energy increases of 2.5 to 2.9 kcal/mol for the MP2/aug-cc-pVTZ calculations and 2.7 to 4.3 kcal/mol for the B3LYP/6-311++G(d,p) calculations.

Table I. Calculated Energy Minimum and Position for Individual Calculations

Increases in HOO angle beyond the calculated minimum energy for a given PES result in energy increases from 5.4 to 6.5 kcal/mol for the MP2/aug-cc-pVTZ calculations and 7.4 to 8.1 kcal/mol for the B3LYP/6-311++G(d,p) calculations. Table II catalogs the effect on dimer energy of O-O distance lengthening for a fixed H-bond angle and H-bond angle distortion for a fixed O-O separation for each chemistry/basis set, solvation state, and geometry combination used. The difference in the effects of O-O distance lengthening and H-bond angle distortion can also be seen in the 2-dimensional energy maps in Figures 2B and 3B, where the “cold,” or low energy, portions of the energy surface are restricted to H-bond angles below approximately 50° while the higher energy regions of the surface are all found in the cases of more substantially bent H-bonds. In all cases, shortening of the O-O distance below 0.28 nm causes an abrupt increase in system energy due to repulsion.

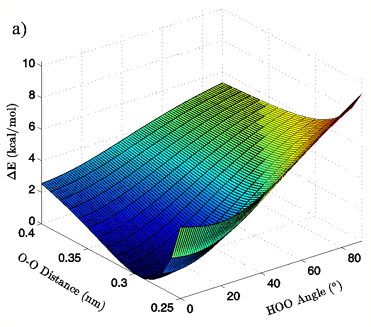
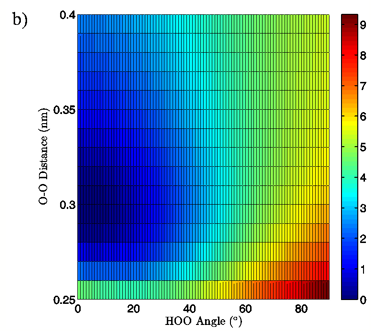
Figure 2: 3D (a) and 2D (b) views of the calculated energy landscape for the MP2/aug-cc-pVTZ planar vacuum dimer. Energies are relative to the calculated minimum for this particular PES.

O-O Energy Fits

In Figures 4A and 5A, 2-dimensional plots of the dimer system energy versus O-O distance for the MP2/aug-cc-pVTZ planar and tetrahedral vacuum cases are shown for H-bond angles of 0° to 90° at 5° intervals. Figures 4B and 5B show R2 values obtained from fitting a standard Morse potential to every calculated angle’s energy dependence on O-O distance. These slices, taken along the O-O distance dimension of the 3-dimensional energy surfaces, reveal energy profiles that fit extremely well to a Morse potential energy function for small H-bond angles. Though the exact point where “Morseness” breaks down is difficult to quantify, significant deviations in the R2 value of the fits begin to occur at approximately 50-65° for the vacuum calculations (Figures 4B and 5B) and 30-40° for the PCM calculations (not shown). These angles are also where errors increase greatly for the individual Morse fit parameters (not shown) and where the energy curves cease to have a local minimum. For example, the well depth parameter in the Morse function, De, fits with a 95% confidence interval of hundredths of a kcal/mol for all angles up to 60° for the MP2/aug-cc-pVTZ planar vacuum case, at which point the confidence intervals grow to several tenths of a kcal/mol. By the time the H-bond is distorted to 73° fits are exceptionally poor, yielding confidence intervals of more than 1 kcal/mol. Similar trends were obtained for the other combinations of model chemistry/basis set, solvation state, and dimer geometry, with only the particular angle at which Morseness breaks down changing with the PES in question.

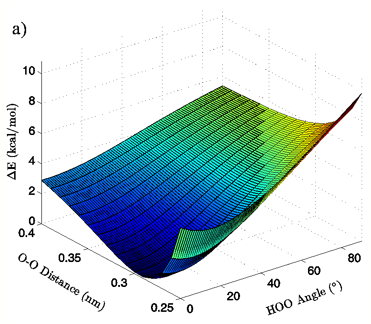
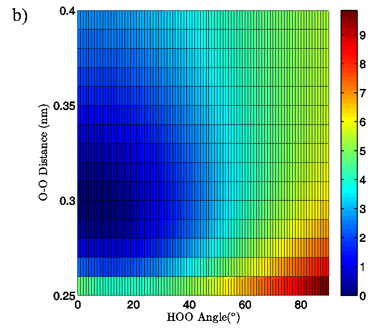
Figure 3: 3D (a) and 2D (b) views of the calculated energy landscape for the MP2/aug-cc-pVTZ tetrahedral vacuum dimer. Energies are relative to the calculated minimum for this particular PES.

Charges

a) ΔAngle energies were determined by subtracting the energy of the minimum energy geometry for a particular PES from the energy of the geometry with the same O-O distance but ∠HOO = 90°.

b) ΔDistance energies were determined by subtracting the energy of the minimum energy geometry for a particular PES from the energy of the geometry with the same H-bond angle but O-O = 0.40 nm.

Table II. Change in System Energy, Relative to the Minimum Energy Geometry for a Given PES, with Increase in H-Bond Angle or O-O Distance

Discussion

There has been a tremendous amount of research and discussion on the nature of H-bonds over the years. The H-bond itself is still so poorly understood at the fundamental level that it remains unclear exactly what geometry constitutes a “real” H-bond, with a variety of distance and angle cutoffs used to specify H-bonding interactions. This question is deeper than mere nomenclature and instead points to the underlying question, that being “what is the fundamental nature of the H-bond and how do we know when one exists?” In this study we chose to focus on one of the most commonly used theoretical instances of H-bonding in chemistry, the single H-bond between two water molecules in which one water molecule’s oxygen atom accepts a single H-bond from an H-bond donor water molecule. By standardizing the internal molecular geometries we were able to examine in detail the effect that intermolecular orientation, specifically the O-O separation and the H-bond angle, had on a number of quantum mechanically calculable quantities. Though internal fluctuations in OH bond length and HOH angle are certainly important in the energetics of real water H-bonds, it is only through the use of the rigid monomer approximation that we were able to elucidate the relative and independent effects of H-bond angle and O-O distance on the single intermolecular H-bond.

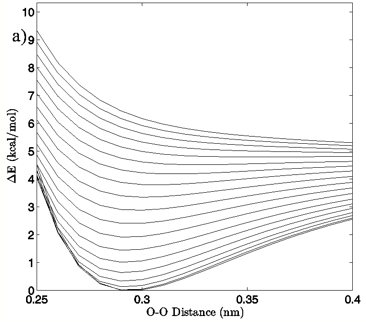
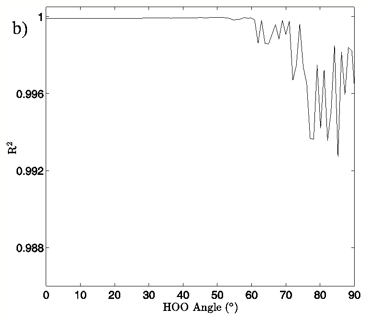
Figure 4: a) The change in system energy with O-O distance at fixed H-bond angle for the MP2/aug-cc-pVTZ planar vacuum case. Energy curves are shown for H-bond angles from 0° to 90° at 5° intervals, with the 0° curve being lowest in energy and 90° being highest in the figure. b) R² values obtained from fitting a standard Morse potential to every calculated angle’s energy dependence on O-O distance.

The first calculated quantity of interest in any quantum mechanical system is the energy, and the 3-dimensional and 2-dimensional energy landscapes shown in Figures 2 and 3 clearly show that H-bond angle has a far more pronounced effect on system energy than does the linear separation of the individual water molecules. At the known O-O distance for liquid water, approximately 0.28 nm (Strassle et al. 2006), the MP2/aug-cc-pVTZ dimers show energy increases of between 5.4 and 6.4 kcal/mol when distorting the H-bond angle from 0° to 90°, while lengthening the O-O distance to 0.40 nm with a fixed H-bond angle of 0° increases the energy by between 2.5 and 2.8 kcal/mol, or about half the effect seen upon increasing the H-bond angle. The B3LYP/6-311++G(d,p) dimers, though presenting a slightly more curved energy landscape, show the same behavior, with energy increases of 7.0 to 7.9 kcal/mol due to angular distortion for a dimer with the O-O distance fixed at 0.28 nm and only 2.7 to 4.2 kcal/mol for increase in O-O separation to 0.28 nm with a fixed H-bond angle of 0°. For both the MP2/aug-cc-pVTZ and the B3LYP/6-311++G(d,p) calculations, the PCM solvation method serves to flatten the PES at large H-bond angles, due to interaction between the H-bond donor hydrogen atom and the reaction field. In liquid water O-O separation of first shell water molecules is tightly confined, as can be seen in the narrow and well defined peak at 0.28 nm in the oxygen radial distribution. The computational results presented here seem to indicate that the small fluctuations in O-O separation, and therefore H-bond length, which are possible in condensed phase water are likely to have only very small effects on H-bond energy and that the principal factor in determining H-bond strength is in fact H-bond angle.

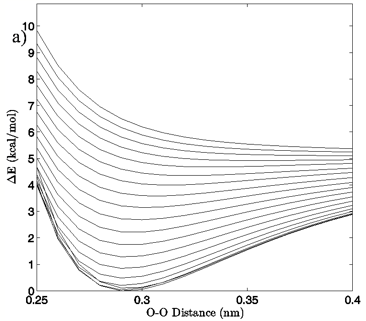
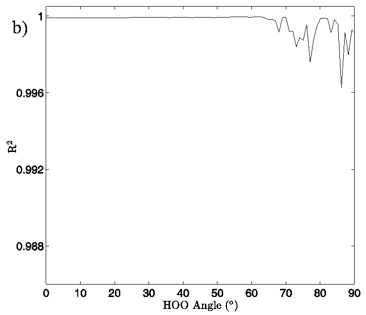
Figure 5: a) The change in system energy with O-O distance at fixed H-bond angle for the MP2/aug-cc-pVTZ tetrahedral vacuum case. Energy curves are shown for H-bond angles from 0° to 90° at 5° intervals, proceeding from bottom to top in the order 5°, 10°, 0°, 15°, 20°, etc. up to 90°. b) R² values obtained from fitting a standard Morse potential to every calculated angle’s energy dependence on O-O distance.

Examination of the slices along the H-bond distance dimension of the energy landscape also points to the critical role that H-bond angle plays in the H-bonding interaction of the water dimer, in addition to defining a range over which we may differentiate a strong H-bond from a bent or broken H-bond. The H-bond distance versus energy plots show Morse-like distance dependence, which is typically indicative of covalent interactions, up to about 50-65° for the vacuum calculations and 30-40° for the PCM calculations. The well depth of the energy profiles is at its deepest for small H-bond angles and gradually grows shallower as the H-bond angle distorts. At the point where there ceases to be a local minimum, the interaction is entirely repulsive, and a Morse fit becomes nonsensical. Though a water dimer with fixed bond lengths and angles is a simplification of real water H-bonding it is not difficult to envision a similar, though likely more complex, H-bonding cutoff scheme for H-bonds in liquid water.

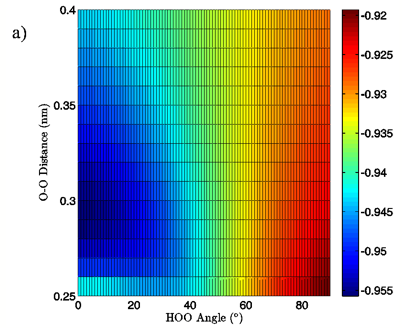
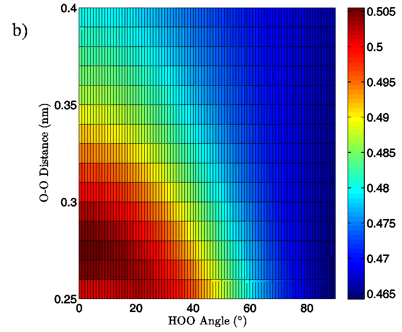
Figure 6: 2D charge landscapes for the H-bond accepting oxygen atom (a) and H-bond donating hydrogen atom (b) for the MP2/aug-cc-pVTZ planar vacuum water dimer case.

MP2/aug-cc-pVTZ and B3LYP/6-311++G(d,p) calculations, both for the vacuum and PCM cases, similarly point to H-bond angle having a much larger effect on the H-bond acceptor water molecule’s oxygen and H-bond donor hydrogen charges than does the H-bond distance. For the MP2/aug-cc-pVTZ vacuum calculations, for instance, the donor hydrogen charge decreases by 0.033 e to 0.038 e when the angle of the H-bond is increased from 0° to 90° with the O-O distance fixed at 0.28 nm, whereas the increase of H-bond distance from 0.28 nm to 0.40 nm at a 0° H-bond angle causes a decrease in charge of only 0.023 to 0.024 e (data read from Figures 6B and 7B). The same trend in the data is seen for all of the vacuum calculations, independent of dimer geometry or model chemistry/basis set. For the PCM calculations however, this finding is reversed, with O-O separation having the greater effect on the charge of the H-bond donor hydrogen atom due to strong interaction between it and the solvation reaction field.

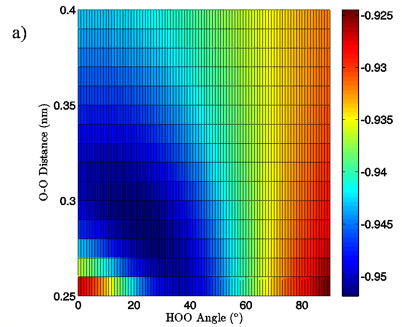
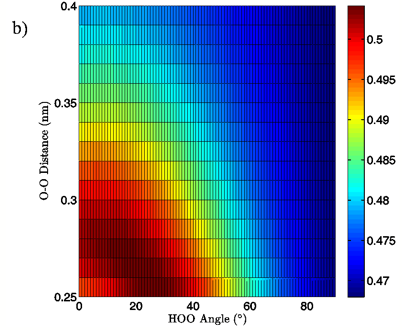
Figure 7: 2D charge landscapes for the H-bond accepting oxygen atom (a) and H-bond donating hydrogen atom (b) for the MP2/aug-cc-pVTZ tetrahedral vacuum water dimer case.

The MP2/aug-cc-pVTZ vacuum dimer H-bond acceptor oxygen atoms show a change in charge similar to that seen for the H-bond donor hydrogen atom for both dimer geometries, with an increase of 0.021 to 0.033 e upon angular deviation at a fixed O-O distance of 0.28 nm and only 0.007 to 0.013 e when the O-O separation is lengthened to its maximum value while the H-bond angle is held at 0° (data read from Figures 6A and 7A). In fact, for all of the calculations, independent of model chemistry, solvation state, or dimer geometry, deviation of the H-bond angle to 90° with the O-O distance fixed at 0.28 nm has over twice the effect on oxygen charge that keeping the H-bond angle at 0° and separating the oxygen atoms to 0.40 nm does. Though the exact charge magnitudes change somewhat based on the geometry, model chemistry and basis set, and solvation state used the trend is consistent throughout the calculations, indicating that H-bond angle has a much greater effect on the charge of the two H-bonding atoms than does their radial separation. The only exception to this finding is for the aforementioned H-bond donor hydrogen atom involved in PCM calculations.

a) ΔAngle charges were determined by subtracting the charge of the minimum energy geometry for a particular PES from the charge of the geometry with the same O-O distance but ∠HOO = 90°.

b) ΔDistance charge were determined by subtracting the charge of the minimum energy geometry for a particular PES from the charge of the geometry with the same H-bond angle but O-O = 0.40 nm.

Table III. Change in Charge with Increase in O-O Distance and H-Bond Angle

Conclusions

This paper presents a novel result on the influence of H-bond angle on the energetics and charges of a singly H-bonded water dimer. We have described what we believe to be new evidence and insight into what may well be a general feature of H-bond response to changes in basic donor/acceptor intermolecular geometry. By simplifying the internal geometries of two water molecules we were able to examine in detail the dependency of energy and charge on H-bond angle and O-O separation. We found that H-bond angle appears to play the largest part in determining H-bond strength with O-O distance, and therefore H-bond length, accounting for a much smaller part. Though these results are not immediately applicable to the more complex case of multiple H-bond donation and acceptance found in liquid water, it may be that the sort of H-bond dependence found here for a single H-bond is still relevant at some level to a condensed phase H-bonding liquid like water.

Acknowledgment

This research was supported by USDA Cooperative State Research, Education and Extension Service, Grant 2005-35503-16151.

References

Barbiellini, B; Shukla, A (2002). Ab initio calculations of the hydrogen bond. Phys Rev B, 66: 235101/1-235101/5.

Becke, AD (1993). Density-functional thermochemistry. III. The role of exact exchange. J Chem Phys 98: 5648-5652.

Boese, AD; Martin, JML; Klopper, W (2007). Basis Set Limit Coupled Cluster Study of H-Bonded Systems and Assessment of More Approximate Methods. J Phys Chem A 111: 11122-11133.

Boys, SF; Bernardi, F (1970), The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol Phys 19: 553-566.

Brady, JW; Mason, PE; Neilson, GW; Enderby, JE; Saboungi, ML; Ueda, K; Naidoo, KJ (2006). Modelling Molecular Structure and Reactivity in Biological Systems, Royal Society of Chemistry: London: 76-82.

Bukowski, R; Szalewicz, K; Groenenboom, GC; van der Avoird, A (2008), Polarizable interaction potential for water from coupled cluster calculations. I. Analysis of dimer potential energy surface. J Chem Phys 128: 094313/1-094313/15.

Cossi, M; Rega, N; Scalmani, G; Barone, V (2003), Energies, structures, and electronic properties of molecules in solution with the C-PCM solvation model. J Comput Chem 24: 669-681.

Creighton, TE (1991), Stability of folded conformations. Curr Opin Struct Biol 1: 5-16.

Curtiss, LA; Frurip, DJ; Blander, M (1979), Studies of molecular association in H2O and D2O vapors by measurement of thermal conductivity. J Chem Phys 71: 2703-2711.

Dashnau, JL; Nucci, NV; Sharp, KA; Vanderkooi, JM (2006), Hydrogen Bonding and the Cryoprotective Properties of Glycerol/Water Mixtures. J Phys Chem B 110: 13670-13677.

Dashnau, JL; Conlin, LK; Nelson, HCM; Vanderkooi, JM (2008), Water structure in vitro and within Saccharomyces cerevisiae yeast cells under conditions of heat shock. Biochim Biophys Acta 1780: 41-50.

Davidson, ER (1996), Comment on “Comment on Dunning’s correlation-consistent basis sets”. Chem Phys Lett 260: 514-518.

Frisch MJT, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Montgomery, Jr., J. A.; Vreven, T.; Kudin, K. N.; Burant, J. C.; Millam, J. M.; Iyengar, S. S.; Tomasi, J.; Barone, V.; Mennucci, B.; Cossi, M.; Scalmani, G.; Rega, N.; Petersson, G. A.; Nakatsuji, H.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Klene, M.; Li, X.; Knox, J. E.; Hratchian, H. P.; Cross, J. B.; Bakken, V.; Adamo, C.; Jaramillo, J.; Gomperts, R.; Stratmann, R. E.; Yazyev, O.; Austin, A. J.; Cammi, R.; Pomelli, C.; Ochterski, J. W.; Ayala, P. Y.; Morokuma, K.; Voth, G. A.; Salvador, P.; Dannenberg, J. J.; Zakrzewski, V. G.; Dapprich, S.; Daniels, A. D.; Strain, M. C.; Farkas, O.; Malick, D. K.; Rabuck, A. D.; Raghavachari, K.; Foresman, J. B.; Ortiz, J. V.; Cui, Q.; Baboul, A. G.; Clifford, S.; Cioslowski, J.; Stefanov, B. B.; Liu, G.; Liashenko, A.; Piskorz, P.; Komaromi, I.; Martin, R. L.; Fox, D. J.; Keith, T.; Al-Laham, M. A.; Peng, C. Y.; Nanayakkara, A.; Challacombe, M.; Gill, P. M. W.; Johnson, B.; Chen, W.; Wong, M. W.; Gonzalez, C.; and Pople, J. A., (2004), Gaussian 03, Revision D.01: Gaussian, Inc.

Gallagher, KR; Sharp, KA (2003), A New Angle on Heat Capacity Changes in Hydrophobic Solvation. J Am Chem Soc 125: 9853-9860.

Head-Gordon, M; Pople, JA; Frisch, MJ (1988), MP2 energy evaluation by direct methods. Chem Phys Lett 153: 503-506.

Huang, X; Braams, BJ; Bowman, JM; Kelly, REA; Tennyson, J; Groenenboom, GC; van der Avoird, A (2008), New ab initio potential energy surface and the vibration-rotation-tunneling levels of (H2O)2 and (D2O)2. J Chem Phys 128: 034312/1-034312/9.

Hura, G; Sorenson, JM; Glaeser, RM; Head-Gordon, T (2000), A high-quality x-ray scattering experiment on liquid water at ambient conditions. J Chem Phys 113: 9140-9148.

Inada, Y; Orita, H (2007), Efficiency of numerical basis sets for predicting the binding energies of hydrogen bonded complexes: evidence of small basis set superposition error compared to Gaussian basis sets. J Comput Chem 29: 225-232.

Isaacs, ED; Shukla, A; Platzman, PM; Hamann, DR; Barbiellini, B; Tulk, CA (1999), Covalency of the Hydrogen Bond in Ice: A Direct X-Ray Measurement. Phys Rev Lett, 82: 600-603.

Isaacs, ED; Shukla, A; Platzman, PM; Hamann , DR; Barbiellini, B; Tulk, CA (2000), Compton scattering evidence for covalency of the hydrogen bond in ice. J Phys Chem Solids 61: 403-406.

Kendall, RA; Dunning, TH, Jr.; Harrison, RJ (1992), Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J Chem Phys 96: 6796-6806.

Krishnan, R; Binkley, JS; Seeger, R; Pople, JA (1980), Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. J Chem Phys 72: 650-654.

Kumar, R; Schmidt, JR; Skinner, JL (2007), Hydrogen bonding definitions and dynamics in liquid water. J Chem Phys 126: 204107/1-204107/12.

Latimer, WM; Rodebush, WH (1920), Polarity and ionization from the standpoint of the Lewis theory of valence. J Am Chem Soc 42: 1419-1433.

Lee, C; Yang, W; Parr, RG (1988), Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys Rev B 37: 785-789.

Lee, JS (2007), Binding energies of hydrogen-bonded complexes from extrapolation with localized basis sets. J Chem Phys 127: 085104/1-085104/5.

Levy, Y; Onuchic, JN (2006), Water mediation in protein folding and molecular recognition. Annu Rev Biophys Biomol Struct 35: 389-415.

Mas, EM; Bukowski, R; Szalewicz, K; Groenenboom, GC; Wormer, PES; van der Avoird, A (2000), Water pair potential of near spectroscopic accuracy. I. Analysis of potential surface and virial coefficients. J Chem Phys 113: 6687-6701.

Miehlich, B; Savin, A; Stoll, H; Preuss, H (1989), Results obtained with the correlation energy density functionals of Becke and Lee, Yang and Parr. Chem Phys Lett 157: 200-206.

Narten, AH; Levy, HA (1971), Liquid Water: Molecular Correlation Functions from X-Ray Diffraction. J Chem Phys 55: 2263-2269.

Nucci, NV; Vanderkooi, JM (2005), Temperature Dependence of Hydrogen Bonding and Freezing Behavior of Water in Reverse Micelles. J Phys Chem B 109: 18301-18309.

Odutola, JA; Dyke, TR (1980), Partially deuterated water dimers: microwave spectra and structure. J Chem Phys, 72: 5062-5070.

Oleinikova, A; Brovchenko, I; Smolin, N; Krukau, A; Geiger, A; Winter, R (2005), Percolation Transition of Hydration Water: From Planar Hydrophilic Surfaces to Proteins. Phys Rev Lett 95: 247802/1-247802/4.

Riley, KE; Hobza, P (2007), Assessment of the MP2 Method, along with Several Basis Sets, for the Computation of Interaction Energies of Biologically Relevant Hydrogen Bonded and Dispersion Bound Complexes. J Phys Chem A 111: 8257-8263.

Rives, AB; Weinhold, F (1980), Natural hybrid orbitals: ab initio SCF and CI results for carbon monoxide and nickel carbonyl (NiCO). Int J Quantum Chem 14: 201-209.

Santra, B; Michaelides, A; Scheffler, M (2007), On the accuracy of density-functional theory exchange-correlation functionals for H bonds in small water clusters: Benchmarks approaching the complete basis set limit. J Chem Phys 127: 184104/1-184104/9.

Scheiner, S (1994), AB Initio Studies of Hydrogen Bonds: The Water Dimer Paradigm. Annu Rev Phys Chem 45: 23-56.

Schutz, M; Brdarski, S; Widmark, P-O; Lindh, R; Karlstrom, G (1997), The water dimer interaction energy: Convergence to the basis set limit at the correlated level. J Chem Phys, 107: 4597-4605.

Scott, JN; Nucci, NV; Vanderkooi, JM (2008), Changes in Water Structure Induced by the Guanidinium Cation and Implications for Protein Denaturation. J Phys Chem A 112: 10939-10948.

Shank, A; Wang, Y; Kaledin, A; Braams, BJ; Bowman, JM (2009), Accurate ab initio and “hybrid” potential energy surfaces, intramolecular vibrational energies, and classical ir spectrum of the water dimer. J Chem Phys 130: 144314/1-144314/11.

Sharp, KA; Madan, B; Manas, E; Vanderkooi, JM (2001), Water structure changes induced by hydrophobic and polar solutes revealed by simulations and infrared spectroscopy. J Chem Phys 114: 1791-1796.

Sharp, KA; Vanderkooi, JM (2009), Water in the Half Shell: Structure of Water, Focusing on Angular Structure and Solvation. Acc Chem Res, (in press).

Silvestrelli, PL; Parrinello, M (1999), Structural, electronic, and bonding properties of liquid water from first principles. J Chem Phys 111: 3572-3580.

Simon, S; Duran, M; Dannenberg, JJ (1996), How does basis set superposition error change the potential surfaces for hydrogen-bonded dimers?, J Chem Phys 105: 11024-11031.

Smith, JD; Cappa, CD; Wilson, KR; Messer, BM; Cohen, RC; Saykally, RJ (2004), Energetics of Hydrogen Bond Network Rearrangements in Liquid Water. Science 306: 851-853.

Soper, AK (2000), The radial distribution functions of water and ice from 220 to 673 K and at pressures up to 400 MPa. Chem Phys 258: 121-137.

Soper, AK; Phillips, MG (1986), A new determination of the structure of water at 25°C. Chem Phys 107: 47-60.

Sorin, EJ; Rhee, YM; Shirts, MR; Pande, VS (2006), The Solvation Interface is a Determining Factor in Peptide Conformational Preferences. J Mol Biol 356: 248-256.

Strassle, T; Saitta, AM; Le Godec, Y; Hamel, G; Klotz, S; Loveday, JS; Nelmes, RJ (2006), Structure of Dense Liquid Water by Neutron Scattering to 6..5 GPa and 670 K. Phys Rev Lett 96: 067801/1-067801/4.

Tschumper, GS; Leininger, ML; Hoffman, BC; Valeev, EF; Schaefer Iii, HF; Quack, M (2002), Anchoring the water dimer potential energy surface with explicitly correlated computations and focal point analyses. J Chem Phys 116: 690-701.

Vanderkooi, JM; Dashnau, JL; Zelent, B (2005), Temperature excursion infrared (TEIR) spectroscopy used to study hydrogen bonding between water and biomolecules. Biochim Biophys Acta Proteins Proteomics 1749: 214-233.

Wang, Y; Carter, S; Braams, BJ; Bowman, JM (2008), MULTIMODE quantum calculations of intramolecular vibrational energies of the water dimer and trimer using ab initio-based potential energy surfaces. J Chem Phys 128: 071101/1-071101/5.

Weinhold, F; Robert, LB; David, B (2005), Resonance Character of Hydrogen-bonding Interactions in Water and Other H-bonded Species. Adv Protein Chem 72: 121-155.

Wernet, P; Nordlund, D; Bergmann, U; Cavalleri, M; Odelius, M; Ogasawara, H; Naeslund, LA; Hirsch, TK; Ojamaee, L; Glatzel, P; Pettersson, LGM; Nilsson, A (2004), The Structure of the First Coordination Shell in Liquid Water. Science 304: 995-999.

Discussion with Reviewers

Ralph Dougherty¹: Drs. Scott and Vanderkooi, in view of the collection of evidence that shows hydrogen bonds to be covalent (see, e.g., J. Li, Inelastic neutron scattering studies of hydrogen bonding in ices, J. Chem. Phys., 105 (1996) 6733-6755; E. D. Isaacs, A. Shukla, P. M. Platzman, D. R. Hamann, B. Barbiellini, C. A. Tulk, Covalency of the Hydrogen Bond in Ice: A Direct X-Ray Measurement, Phys. Rev. Letters, 82 (1999) 600-603) did the orbital overlap between the two water molecules correlate strongly with the changes in potential?

Nathan Scott and Jane Vanderkooi: To attempt to answer this question we re-ran a subset of our original calculations such that orbital overlap information and the MP2-based electron density were output by Gaussian. We also generated potential energy grid data in the form of a cube file based on the MP2-based electron density. Given the strong support for Dyke and Odutula’s dimer geometry outlined in the response to question 2 below, we chose to examine the MP2 vacuum tetrahedral calculations at every 10° (0°, 10°, 20°, etc.) and at O-O distances of 0.28 nm, 0.31 nm, 0.34 nm, 0.37 nm, and 0.40 nm.

To determine which molecular orbitals we should concentrate on, C2 population analysis was performed for all of the valence orbitals in order to analyze their individual atomic contributions to orbital mixing. Orbitals 6 and 8 (at approximately -18.6 eV and -15.1 eV, respectively, for the case where the HOO angle is 0° and the O-O separation is 0.28 nm) were found to have significant contribution to their overall electron occupation from the H-bond donor hydrogen atom and the H-bond acceptor oxygen atom. These are also the two oribitals that when simply visualized using molecular orbital grid data appear to have the most H-bonding character.

Plots of the atomic orbital overlap data were visualized using the freely available GaussSum software package (N. M. O’Boyle, A. L. Tenderholt and K. M. Langner, cclib: A library for package-independent computational chemistry algorithms, J. Comp. Chem., 29, (2008) 839-845). For molecular orbital 6, the H-bond donor H and H-bond acceptor O orbital overlap (hereafter referred to simply as overlap 1) was bonding in nature (i.e. positive), as was the orbital overlap between the H-bond donor O and H-bond acceptor O (hereafter referred to as overlap 2). As O-O distance is increased, both overlap 1 and 2 decrease dramatically. At an O-O separation of 0.28 nm, as the H-bond angle is increased from 0° to 30°, overlap 1 starts out about twice as large as overlap 2 and decreases quickly while overlap 2 decreases very slowly. At 50° overlap 1 and overlap 2 are nearly equal, and as the H-bond angle is further increased overlap 1 finally falls below overlap 2. At the final angle of 90° both overlaps have shrunk nearly to zero.

The orbital overlap data for molecular orbital 8 shows that overlaps 1 and 2 shrink quickly with increase in O-O distance, falling off to nearly zero overlap at 0.37 nm. At 0° H-bond angle and 0.28 nm O-O distance, overlap 1 is bonding in nature while overlap 2 is antibonding. As H-bond angle is increased, overlap 1 becomes less bonding (becoming antibonding at 20°) and overlap 2 becomes less antibonding (becoming bonding in character at 30°). At all H-bond angles except 0°, the combination of the 2 overlaps is more antibonding in nature than it is bonding, indicating that molecular orbital 6 is the principle H-bonding orbital in these calculations.

The correlation between the orbital overlaps and electrostatic potential is far from certain in these results but it does appear at least possible. Even for the linear H-bond, negative electrostatic potential begins to intercede between the H-bond donor H and H-bond acceptor O at an O-O separation of about 0.34 nm. At this distance orbital overlaps 1 and 2 have nearly vanished to zero. At a fixed O-O distance of 0.28 nm, negative potential begins to appear between the water molecules at about 50°. This is the same angle at which orbital overlaps 1 and 2 of molecular orbital 6 have shrunk to become equal, and very small relative to their values at the H-bond angle of 0°.

This is an intriguing question and probably warrants a more thorough study, but it would not be surprising to find that the two quantities, H-bonding orbital overlap and electrostatic potential, are in fact closely correlated.

Dougherty: Would you specifically compare the results of this work with the microwave structure of the water dimer obtained by Dyke and his co-workers?

Scott and Vanderkooi: Our results appear to support the experimental data and analysis of Dyke and Odutola. As noted in our article, for our tetrahedrally coordinated dimer calculations we used a θa angle (Dyke’s notation for the Euler angle between the OH donor vector and the plane of the acceptor water molecule) of 57°, and this value was chosen specifically based on Dyke’s work. However, our OH bond lengths and HOH angles were chosen to be fixed at 0.0991 nm and 105.5° respectively, quite different from the 0.09572 nm and 104.52° degree rigid rotor model applied by Dyke and Odutola to analyze their microwave spectra and based on much earlier work by Plyler et al. (W. S. Benedict, N. Gailar, and E. K. Plyler, Rotation-Vibration Spectra of Deuterated Water Vapor, J. Chem. Phys., 24 (1956) 1139). As noted in the text, our internal molecular geometry was chosen to more accurately reflect what is believed to be the average values for condensed phase water molecules, rather than those of a gaseous water dimer. Despite the substantial differences between the two rigid models, as can be seen in Table 1, for both tetrahedral vacuum calculations we found the global energy minimum at a position where the dimer oxygen-oxygen separation is 0.29 nm (compare to Dyke’s 0.2976 nm (+0.000/-0.0030 nm)) and a xa angle (Dyke’s notation for the HOO angle) of 6° (compare to Dyke and Odutola’s finding of 6° (+/- 20°)). With only our θa angle fixed at the value specified by Dyke and Odutola, the two dependent variables in our study are extremely close to the experimentally determined values.

Dougherty: Since the structure of liquid water is now known to undergo changes with temperature (see, e.g., C. Huang, K. T. Wikfeldt, T. Tokushima, D. Nordlunda, Y. Harada, U. Bergmann, M. Niebuhr, T. M. Weiss, Y. Horikawa, M. Leetmaa, M. P. Ljungberg, O. Takahashi, A. Lenz, L. Ojamäe, A. P. Lyubartsev, S. Shin, L. G. M. Pettersson, A. Nilsson, Proc. Natl. Acad. Sci., 106 (2009) 15214-15218), would you expect there to be observable variations in water dimer structure, or structure distribution, with temperature?

Scott and Vanderkooi: One would certainly expect there to be changes in water dimer structure with temperature. In particular, rotational levels, which are sure to be populated at all but the lowest temperatures, would distort both the intermolecular H-bond as well as the geometries of the individual water monomers. One of the more impressive and ground breaking parts of Dyke and Odutola’s work was that they were able to produce dimers with rotational temperatures under 20 K, which allowed for very high signal-to-noise data. At increased temperatures it seems unlikely that variations in dimer structure would be observable, due to the large degree of structural heterogeneity. However, though the variations might not be observable, we can reasonably infer that they must still exist.

¹ Professor Emeritus, Department of Chemistry and Biochemistry, Florida State University, Tallahassee, FL, USA