Evidence of Coherent Dynamics in Water Droplets of Waterfalls

Evidence of Coherent Dynamics in Water Droplets of Waterfalls

Madl P1*, Del Giudice E2, Voeikov VL3, Tedeschi A4, Kolarž P5, Gaisberger M6 and Hartl A6

1 University of Salzburg, Material Research and Physics, Hellbrunnerstr. 34 A-5020 Salzburg, Austria
2 Centro Studi Eva Reich, Via Orti 5, Milan, I-20135, Italy 
3 Lomonosov Moscow State University, RUS-119995, Moscow
4 WHITE Holographic Bioresonance, Milan, Italy
5 Institute of Physics, Pregrevica 118, RS-11080 Belgrade
6 Institute of Physiology and Pathophysiology, Paracelsus Medical University, Strubergasse 21, A-5020 Salzburg, Austria

*Correspondence E-mail: [email protected]

Key Words: Charged waterfall-aerosol, Water-coherence, Coherence Domains (CD), Size and charge of CDs, QED

Received June 21st, 2011; Accepted July 1st, 2013; Published July 20th, 2013; Available online October 10th, 2013

doi: 10.14294/WATER.2013.7

 

Abstract

It is the scope of this paper to propose an additional charging mechanism of water-fall generated aerosols. The observations leading to this approach arose from a field study at five waterfalls in the Austrian Alps. Thereby, size distributions of ion clusters, their mobility and their intermediate progenies near waterfalls have been measured with a tandem ion spectrometer consisting of three aspirated Gerdien Cylindrical Ion Detectors (CDI) in combination with a Scanning Mobility Particle Sizer (SMPS).  It was observed that the concentration of negative 0.9-10 nm ions was 2-3 orders of magnitude higher than at the reference points up to several 100s of meters away from the waterfalls. Here we discuss the observed features in a quantum electro-dynamic scheme. We find good agreement between theory and observations obtained in the field, which supports the view that water in this size range is highly structured and coherent.

 

Article Outline

 

Introduction

It has been known for a long time that water falling in waterfalls splits into a fog of tiny droplets whose surface is negatively charged. Measurements near waterfalls demonstrate that negatively charged particle inventories reveal distinct distribution patterns, which are dominated by clusters around 0.6 to 2.5 nm (Laakso et al., 2007) and associated progeny in the 120 nm range. Interestingly, the larger peak appears to be a characteristic phenomenon as we were able to observe these also on other occasions at the falls of Möll and Gartl (Kolarž et al., 2012). If this peak relates to classical (mechanical) origins only, then it should shift and fluctuate according to meteorological conditions, varying splashing modes that induce charging, and other abiotic parameters. The fact that it is stuck more or less at this particular diameter suggests an intrinsic property of aerosolized water bearing predominantly a net negative charge. So far, charges on these droplets are attributed to bursting water films (generated either by impact on surfaces and/or fragmentation of water droplets during free fall – e.g. Zilch et al., 2008) and can easily be detected even with a very simple commercially available air-ion counter. In general, the total charges on the positive side are usually <15% of the total negative charges (Bhattacharyya et al., 2010, Laakso et al., 2007). As has been proposed already some 80 years ago (Currie & Alty, 1929) charge formation could originate from oriented dipoles at the water-vapor boundary. Based on these observations, the charge separation mechanism has been attributed to the presence of an electrical double layer at the surface of the water droplets, where the outermost layers acquire an excess negative charge. Electrophoretic mobility measurements seem to support this view; however, the entire dynamics is not yet fully resolved.

In more recent studies, spectroscopic measurements on the interfacial region of water have shown that 20-30% of molecules exhibit dangling hydrogens, which leave 70-80% of interfacial water dipoles with their positive end directed toward the droplet interior (Paluch, 2000; Parfenyuk, 2002). One could consider however, that charge separation may be induced via a completely different process called electrodynamic ionization (Agostinho et al., 2011). Yet due to the lack of a persisting electrostatic field at the falls and according to their own observation that “positive and negative charges on water droplets do not happen in the presence of strong electric fields”, this option can be excluded. We refer to the provided supplementary material (included below) where we have listed additional material from the Gartl falls, which clearly states that electromagnetic field strengths are quite low. The maximum values, closest to the fall, peak at 1.1 V/m and 59 nT for the electric and magnetic field intensities (Jell, 2005 – unpublished data).

Thus, the present paper, which is a follow-up publication of previously published results from field studies about ion measurements at some waterfalls in the Austrian Alps (Kolarž et al., 2012), proposes a novel charging mechanism of waterfall generated aerosols.

 

Materials and Methods

The experimental setup included – among other instruments, a GPS device and a hand-held Ion Counter – two essential units that have been operated in tandem mode. One set regards a triplet of fully self-contained aspirated Gerdian Cylindrical Ion Detectors (CDI) – each assigned to discrete size channel of 0.9, 1.5 and 2.0 nm, whereas the second device regards a Scanning Mobility Particle Sizer (SMPS) that covers a continuous size range of 5.5 to 350 nm. For reasons of readability, the instruments are briefly described, however, for a detailed description of the CDI we refer to Kolarž et al. (2009), and for the SMPS to Madl (2003).

Gerdian Cylindrical Ion Detector (CDI Version 6): The sensor part of the CDI consists of three cylindrical and coaxially arranged electrodes, i.e., a measuring (central), a polarizing and a shielding electrode. A fan ventilates the space between the centermost and middle electrodes. In the inter-electrode space air-ions of desired polarity and mobility are forced by the electric field across the electrostatic gradient to deliver their ion-related charges to the measuring electrode. Detection of the charge is achieved via a Faraday Cup Electrometer (FCE), providing readouts in one second intervals.

The Scanning Mobility Particle Sizer (SMPS), Grimm model 5400 is capable of measuring the size distribution of sub-micrometer range. The particles are classified with a Dynamic Mobility Analyzer (DMA) that – similar to the CDI – utilizes electrical mobility to separate among different aerosol size classes. Particle concentrations, on the other hand are measured with a Condensation Particle Counter (CPC). The SMPS is a self-contained automated system that is controlled via an external computer. The SMPS comes in two versions – one using a M-DMA (5.5-350 nm), and the other one a L-DMA (10-1100 nm). Due to the small size, the former was used as it sufficiently describes the aerosol inventory at the waterfall. In order to maintain the originally present negative charge of waterfall ions, the instrument was operated without the attached neutralizer (241 Amsource). Operating the instrument with the neutralizer would induce a statistical Boltzmann charge distribution, thereby eliminating the aerosol’s original charge. For an in-depth discussion of the pro and cons of the neutralizer in the context of waterfalls, see Kolarž et al. (2012) along with the discussion material provided therein. Together with the auxiliary battery pack, the entire system can be operated autonomously in the field for more than 8 hours in a row.

Field Location & Data Acquisition: Although several falls have been investigated during our field campaign, this particular article focuses only on the data-set collected at the Krimml Falls. This selection is based on several reasons: Krimml provides easier access, has a higher water load and in terms of results, reveal similar properties in charge and size distribution as found with the falls in Gartl and Möll. In addition, results of the former are listed in Kolarž et al. (2012).

Figure 1 depicts the different readings of five sampling locations of a given waterfall (here the one located at Krimml, Salzburg), which are delimited by the closest (next to the waterfall) and the farthest location (the reference point).

Figure 1: Composite plot of the size distribution of negatively charged particles as measured with distance from the waterfall. Indices denote sampling locations at the fall (WF denotes the waterfall; the satellite view reveals the position in the field - Google maps). Size distribution till 2.5 nm recorded with the CDI, particles from 5.5-350 nm with the SMPS instruments (modified from Kolarž et al., 2012).

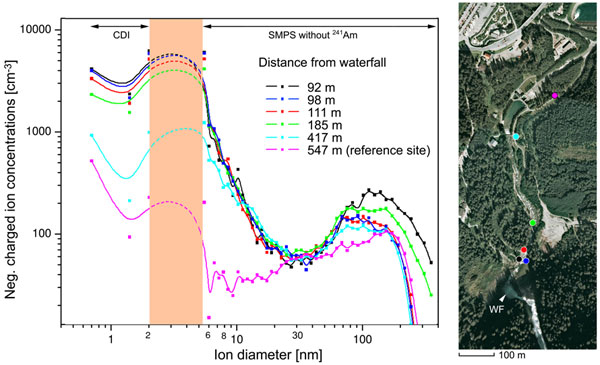
Figure 1: Composite plot of the size distribution of negatively charged particles as measured with distance from the waterfall. Indices denote sampling locations at the fall (WF denotes the waterfall; the satellite view reveals the position in the field – Google maps). Size distribution till 2.5 nm recorded with the CDI, particles from 5.5-350 nm with the SMPS instruments (modified from Kolarž et al., 2012).

 

Transectional data have been obtained by gathering at least three SMPS-scans per location – each scan took about three minutes to cover the full size spectrum from 5.5 to 350 nm, and itself was split into 44 individual size channels. Since each bin consists of nine separate measurements (minus the initial and the last recording – to account for the dynamic measurement principle during switching from one DMA-voltage respectively size bin to the next) an overall set of 924 individual measurements spread over 44 size bins – constitute for the 5.5-530 nm scanning window – have been gathered at each location. At the same time, the CDIs, with its second by second mode of acquisition, logs around 2700 readings for each of the three fixed size bins at the lower end of the particle spectrum, i.e. 0.7, 1.5 and 2.0 nm. Pooled together, each of the five size distributions in that figure is a composite of averaged CDI and SMPS readings with an interpolated regime in-between. Since ions produced from waterworks of high total dissolved solid contents have been found to possess similar motilities as those produced from rainwater (Tammet et al., 2009), lab analysis of water samples have shown that the probes were almost free of organic or mineral contaminants (Alpenverein Krimml, 2010 – unpublished data). The report assigns the Krimmler waterfalls top grade quality (category “A”). An excerpt, with analysis listing three different sampling dates along with the corresponding results has been included as supplementary material.

 

Results

Combining the triplet readings of the CDI with that of the SMPS, one obtains a composite graph as shown in Figure 1. This figure reveals the size distribution of negatively charged particles as mea-sured with increasing distance from the waterfall (92, 98, 111, 185, 417 and 547 m respectively). Therein, only the distribution of negatively charged droplets appears since the instrument is unable to reveal positively charged droplets, which as said in the introduction, account for less than 15% of the total. In the graph, a feature becomes evident, which is astonishing if considered in the framework of the conventional theories of liquid water, namely the presence of aggregates having a size of a few 100 nm. With respect to the smaller aggregates – that measure just a few nanometers and are easily explainable via the conventional framework – the larger ones appear more stable and do not fit the conventional approach. Indeed, these 100 nm aggregates remain remarkably stable with increasing distance from the waterfall. Their presence can still be detected at the reference site roughly half a kilometer away, whereas the number of small aggregates at that location decreases to 1% of the original concentration.

Therefore, the following picture of aerosols originating from a waterfall emerges. Falling water splits into a bimodal size distribution – two families of aggregates with most of them electrically charged. The first family consists of small clusters (a few nanometers), which include at most a few hundreds of water molecules. The second family consists of larger aggregates which, at the normal density of liquid water, include some millions of molecules. Whereas, the small clusters belonging to the first family disappear very fast with distance, the larger aggregates are able to propagate very far from the site of origin. Finally, we should remember that both aggregate types are able to acquire a surface electric charge, which is in most cases negative but could be in some cases also positive. Tammet et al., (2009) attempted to describe a mechanism of how the observed charge separation is induced. According to them, nanometer particles arise out of nucleating burst events, which are associated to the balloelectric effect, i.e. the generation of electric charges by the splashing of water (this effect is also known as the Lenard effect). These authors relate it to the presence of water complexes (e.g. H6O3) and the disruption of the electric double-layer of water. By referring to salt-water, this effect should allocate positive charges on larger droplets and negative charges on smaller ones. Lacking high concentrations of ionic solutes in fresh-water, they have not come up with a satisfactory explanation for fresh-water systems. As mentioned in the introduction, in our previous paper on this topic (Kolarž et al., 2012) we amply referred to Zilch’s mechanical interpretation. Indeed, another research group likewise focusing on this issue, yet using auxiliary technical means aimed at identifying physical mechanisms (in classical terms) of intermediate ion generation (Agostinho et al., 2011), yet the Lenard effect still remains somewhat unsolved and lead us to look towards a quantum mechanical approach.

 

Discussion and Interpretation

In this section we discuss the above observations in a recently proposed theoretical framework, which combines experimental results obtained by Pollack’s group (e.g. Zheng et al., 2003) and the theoretical predictions based on Quantum Electrodynamics (QED) (Preparata, 1995; Del Giudice & Preparata, 1998; Bono et al., 2012; Del Giudice et al., 2010; Del Giudice et al., in press). Zheng et al., (2003) discovered that water close to hydrophilic surfaces exhibits peculiar properties that are different from those of normal bulk water. This water, termed Exclusion-Zone (EZ) water has the following properties (Zheng et al., 2006):

a) It excludes solutes, hence its name;

b) Under stable conditions it forms a thick layer up to 500 μm in width;

c) It appears internally more correlated than normal bulk water, as shown by its viscosity and NMR-response;

d) It absorbs UV-light at 270 nm and is fluorescent if excited by light with this wavelength;

e) Furthermore, Zheng et al. (2009) could show that EZ-water has an electrically charged surface that has the same sign of charge as the adjacent solid surface. EZ-water close to a negatively charged surface acquires a negative surface charge, whereas positive charges (protons) can be found on the opposite side of the EZ-layer. The contrary occurs when the surface charge is positive.

In fact, the last property (e) appears quite mysterious in the framework of conventional theories, and seems to contra-dict the general law of electrostatics, since like electric charges appear to attract and opposite charge appear to repel. A similar phenomenon has been detected in colloids physics where tiny electrically charged microspheres have been found to give rise to metastable crystallites instead of falling apart, as expected by conventional framework (Ise, 2010; Larsen & Grier, 1997). While Ise (2010) traces back these attractions to intermediate counter-ions of opposite charge, Larsen & Grier (1997) did not find any counter-ions present which, in order to remain stable, requires the existence of a many-bodied long-range attraction. In the framework of QED, Del Giudice & Preparata (1998) could demonstrate that this long-range attraction is produced by the emergence of a coherent dynamics in the plasma of charged particles when suitable conditions on the charge density are met.

In the context of QED, it is possible to prove Preparata (1995) by using the following theorem. When an ensemble of a large number N of particles (having an internal spectrum of configurations) is coupled with an electromagnetic field (EMF) such as charges, dipoles, and so on, the fluctuations will exceed a critical density N/V (see also Figure 3) at a given temperature T that is lower than a critical value. Once this happens, the system undergoes a phase transition. The minimum energy state is no longer the state where particles are mutually independent at vanishing values of the EMF. This new minimum energy state is a state where all particles oscillate in unison between two configurations and in phase with the coherent EMF and are thus unable to drift away but are rather self-trapped within the particle ensemble.

This new state has an energy level lower than the previous non-coherent state; the difference is termed “energy gap” and protects the coherent state from destruction induced by thermal collisions. At a finite value of the energy gap, this protection is partial, so that at any value of T lower than the critical value molecules are split in two fractions; the coherent fraction Fc and the non-coherent fraction Fnc (Fc + Fnc = 1) just like it occurs in the Landau model of superfluid Helium. The coherent state extends in a region named Coherence Domain (CD) whose size is the wavelength of the EM-mode responsible for the coherent oscillations. The above theory applies to all molecular species – including water.

Yet still, water is peculiar (Bono et al., 2012; Del Giudice & Preparata, 1998; Del Giudice et al., 2010; Del Giudice et al., in press) in that coherent oscillations of water molecules occur between the ground molecule state, where all electrons are tightly bound and an excited state (12.07 eV) where one electron per molecule is so loosely bound to be considered almost free (Figure 2).

 

Figure 2: Formation of the multimode laser properties due to the energy gap establishes a pumping mechanism. This process results in synchronized excitation and relaxation patterns between the ground level and excitation at 12.07 eV of the involved water molecules (adapted after Chan et al., 1993).

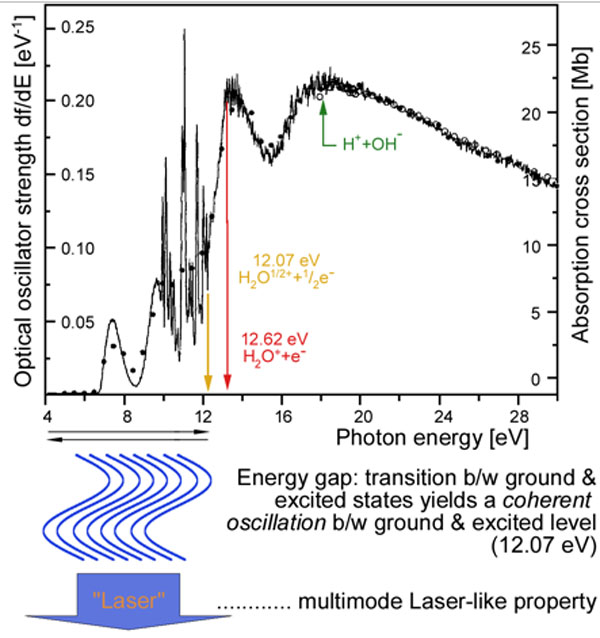
Figure 2: Formation of the multimode laser properties due to the energy gap establishes a pumping mechanism. This process results in synchronized excitation and relaxation patterns between the ground level and excitation at 12.07 eV of the involved water molecules (adapted after Chan et al., 1993).

 

Consequently, water-CDs whose size is the wavelength of 100 nm (Figure 3) correspond to an energy level of 12.07 eV become a reservoir of quasi-free electrons, and at the same time give rise of course to corresponding quasi-free protons. Both Arani et al., (1995) and Preparata (1995) describe the quantum electro-dynamic principles and list the equations that have been used to anticipate such behavior.

 

Figure 3: Formation of coherence domains (CDs) of aerosolized water molecules. The free-floating dipoles start to feel mutually attracted and establish coherent resonance clusters that result in the formation of 75 nm large CDs in which molecules resonate in unison. The newly formed coherent polarizing field becomes entrapped by CDs themselves and reveals a characteristic wavelength of about 100 nm. The formation of CDs is a fundamental property of liquid water and unlike the laser, no energy pumping is required to establish coherence (Arani et al., 1995).

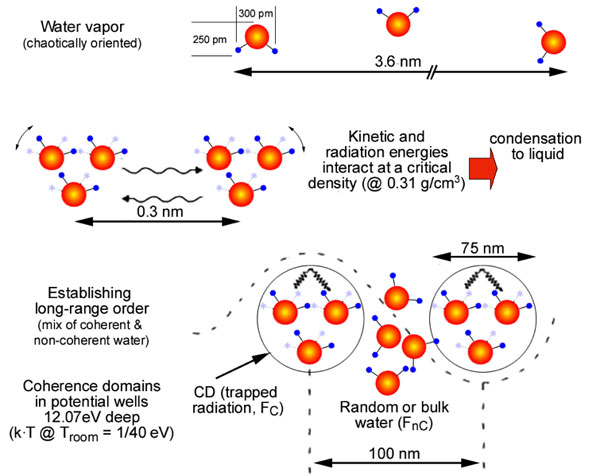
Figure 3: Formation of coherence domains (CDs) of aerosolized water molecules. The free-floating dipoles start to feel mutually attracted and establish coherent resonance clusters that result in the formation of 75 nm large CDs in which molecules resonate in unison. The newly formed coherent polarizing field becomes entrapped by CDs themselves and reveals a characteristic wavelength of about 100 nm. The formation of CDs is a fundamental property of liquid water and unlike the laser, no energy pumping is required to establish coherence (Arani et al., 1995).

 

Later, it has been shown by Buzzacchi et al., (2002) that coherent and non-coherent fractions of non-liquid water are almost equally distributed at room temperature so that a reasonable picture of water is given by an array of CDs having the non-coherent fraction as a very dense gas of molecules squeezed in interstices among CDs (Figure 3). Since non-coherent molecules are squee-zed at very short mutual distances, they are able to form aggregates using short-range static forces, which basically emerge from dipole-dipole interactions. The short-range nature of these interactions form aggregates whose size could not exceed a few nanometers, and therefore could account for the small units detected in our field investigation (see Figure 1). With regard to the smaller aggregates (nano-sized aerosols), the squeezing produced by the cage as a result of the formed CDs disappear, which accounts for the short life-time observed in our field experiment.

Coming back to the coherent fraction, the self-trapped EMF on the CD-boundaries gives rise to a repulsive gradient force (Marchettini et al., 2010) that is proportional to the EMF-gradient and inversely proportional to the mass of the particle acted upon by the field. Consequently, electrons, which are several thousand times lighter than nuclei, are pushed towards the boundaries of CDs whereas protons remain inside. CDs in a sense appear as “giant atoms”.

This said, it is now possible to discuss the interaction of water with hydrophilic surfaces. The attraction between water molecules and surface substrate shields the molecules from the disrupting effect of collisions, so that water close to such a surface is mainly coherent. Since foreign molecules are unable to resonate with the intrinsic frequency of the CDs, they are excluded from CDs and consequently disappear from this region. Therefore, QED-theory provides a simple explanation of the phenomenon of solute exclusion, which is not understandable when relying on the conventional framework.

A yet unresolved issue regards the problem of the sign of the electric charge dispersed on hydrophilic surfaces. We assume that the charges are stuck on the surface but able to oscillate as a plasma. Starting with negative charges, which are ultimately electrons, a new kind of coherence becomes possible (Del Giudice et al., in press). A mixed coherence state involving both quasi-free electrons from the surface of water-CDs and electrons originating from the surface substrate (EZ-water) will result in a further decrease of energy making the system more stable. Let us recall, that the plasma frequency is proportional to the square root of the charge density. The number of electrons on the solid surface, and therefore its plasma frequency is fixed, whereas the number of electrons of water-CDs involved in the process can be determined by the requirement that its plasma frequency should be equal – in order to achieve coherence – to the plasma frequency of the solid surface. This requirement determines the depth of the layer of water involved in the process.

In the case of a positive charge of the surface, the requirement of having coherence – which minimizes the energy of the system – induces reshuffling of the CD-structure, which pushes the quasi-free protons towards the surface, whereas quasi-free electrons are now forced inwards.

In both cases (positive and negative surface charge) the energy gap produced by the onset of coherence decreases the binding of the charge on the solid surface with their corresponding matrix. This facilitates breakage of the bonds above a critical threshold value induced by environmental variables such as flow-speed and turbulence. The water of the river becomes therefore an ensemble of turbulently mixed charged subunits.

 

Conclusion

With the concepts presented above it is possible to merge and summarize the field experiments with the outlined theory, and at the same time address the problem of negatively charged aerosols originating from waterfalls. In a river, solid surfaces such as rocks constituting the river-bed and suspended solid particles (sand, prokaryotes, protozoa, autotrophic algae) give rise to EZ-water. According to the electric charge present on these solid surfaces, the river can be regarded as an ensemble of flowing coherent CDs made up by both positively and negatively charged entities. When the flow becomes fragmented by the waterfall, the constituting units show up as an aerosol of separated units, each one carrying the electric charge of the prevailing river-flow dynamics.

Since the feature depicted in Figure 1 highlights the existence of aggregates as large as 100 nm, it suggests the presence of aggregates made up of single CDs or of small clusters of them (super-coherent domains). On the other hand, the small aggregates should arise from metastable structures formed by non-coherent molecules as a result of the squeezing property in bulk water.

With this in mind, extended coherence (supercoherence), namely coherence among CDs, emerges as a logical consequence of the biological dynamics, for instance in photosynthesis (Tedeschi, 2010). Actually, coherent water aerosol, as present in waterfalls, has been shown to be beneficial to living organisms such as for the health of exposed individuals (Gaisberger et al., 2012). Similar observations have also been made in gardens (Spinetti, 2010) and open air inhalation spas (Kwasny et al., 2008). Indeed, Chinese traditions such as Tai Ji Quan and Qi Gong exercises are recommended to be performed near water-falls (Watts, 1975). Since coherent water seems to be a fundamental issue in all living organisms, it is very likely that coherent water indeed does promote health. Thus and in accordance with findings published by Voeikov & Del Giudice (2009), the biological relevance of negatively charged particle inhalation will be laid out in a subsequent paper. But it does not stop here as the formation of CDs and their implications reach well beyond medical relevance and may well include such basic phenomena as stability of sand-water mix-tures, reduction of friction at the liquid-solid interface, and atmospheric lightning.

 

Acknowledgements

The current research project was funded by the Salzburg National Park Fund along with funds from the EU program for rural development. It was partially also supported by MES Serbia No: 171020, 45003.

References

Agostinho LLF, Fuchs EC, Metz SJ, Yurteri CU, Marijnissen JCM (2011) Reverse movement and coalescence of water microdroplets in electrohydrodynamic atomization. Phys Rev. E, 84: 026317-1-12.

Arani R, Bono I, Del Giudice E, Preparata G. (1995) QED Coherence and the Thermodynamics of Water. Intl. J. Mod. Phys.B., 9: 1813-1841.

Bhattacharyya I, Maze JT, Ewing GE, Jarrold MF. (2010) Charge Separation from the Bursting of Bubbles on Water. J. of Physical Chemistry A., 115(23): 5723-5728.

Bono I, Del Giudice E, Gamberane L, Henry M. (2012) Emergence of Coherent Structure of Liquid Water. Water, 4: 510-532.

Buzzacchi M, Del Giudice E, Preparata G. (2002) Coherence of the glassy state. Int. J. Mod. Phys. B., 16: 3761-3786.

Chan WF, Cooper G, Brion CE. (1993) The electronic spectrum of Water in the discrete and continuum regions. Absolute optical oscillator strengths for photoabsorption (6-200 eV). Chemical Physics, 178: 387-400.

Currie BW, Alty T. (1929) Absorption at a Water Surface. Part 1. Proc. R. Soc. Ldn, 122: 622–633.

Del Giudice E, Preparata G. (1998) Electrodynamical like charges attractions in metastable colloid crystallites. Modern Phys. Lett. B. 12: 991-885.

Del Giudice E, Spinetti PR, Tedeschi A. (2010) Water Dynamics at the Roots of the Metamorphosis in Living Organisms. Water, 2: 566-586.

Del Giudice E, Voeikov VL, Tedeschi A, Vitiello G. (in press) Coherence in aqueous systems: origin, properties and consequences for the living state. In: Fels D. & Cifra M. (eds) Fields of the Cells, Basel, CH.

Gaisberger M, Šanović R, Dobias H, Kolarž P, Moder A, Thalhamer J, Selimović A, Huttegger I, Ritter M, Hartl A. (2012) Effects of Ionized Waterfall Aerosol on Pediatric Allergic Asthma. Journal of Asthma, 49(8): 830-838.

Ise N (2010) Like likes like: counterion-mediated attraction in macroionic and colloidal interaction. Phys. Chem. Chem. Phys.: 12: 10279-10287.

Kolarž PM, Filipovic DM, Marinkovic BP. (2009) Daily variations of indoor air-ion and radon concentrations. Applied Radiation and Isotopes, 67: 2062–2067.

Kolarž PM, Gaisberger M, Madl P, Hofmann W, Ritter M, Hartl A (2012) Characterization of ions at Alpine waterfalls. Atmospheric Chemistry and Physics, 12: 3687–3697.

Kwasny F, Madl P, Hofmann W. (2008) Effects of salt-aerosols from a gradierwerk on Inhalation therapy and ambient aerosols. Berichte der Nat-Med-Vereinigung Salzburgs 15: 99-108.

Laakso L, Hirsikko A, Gronholm T, Kulmala M, Luts A, Parts TE (2007) Waterfalls as sources of small charged aerosol particles, Atmos. Chem. Phys., 7, 2271–2275.

Larsen AE, Grier DG (1997) Like charges attractions in metastable colloid crystallites. Nature 385: 230-235.

Madl P. (2003) Instrumental development and application of a Thermodenuder. Diploma Thesis at the QUT (Brisbane, AUS) in corporation with Salzburg University (AUT), Chapter III-3. [02-01-2012]

Marchettini N, Del Giudice E, Voeikov VL, Tiezzi E. (2010) Water: A medium where dissipative structures are produced by a coherent dynamics. J. Theo. Bio., 265: 511-516.

Paluch M. (2000) Electrical Properties of Free Surface of Water and Aqueous Solutions. Adv. Colloid Interface Sci., 84: 27–45.

Parfenyuk VI. (2002) Surface potential at the gas-aqueous solution interface, Colloid J., 64: 588-595.

Preparata G. (1995) Dynamics and Thermodynamics of Water; in: QED Coherence in Matter. World Scientific, Singapore; p. 195-217.

Spinetti PR. (2010) The ecosystem dynamics of the garden. Int. J. Des. Nat. Ecodyn. 5: 49-55.

Tedeschi A. (2010) Is the living dynamics able to change the properties of water? Int. J. Des. Nat. Ecodyn., 5: 60-67.

Voeikov V, Del Giudice E. (2009) Water Respiration – The Basis of the Living State. Water Journal, 1: 52-75.

Watts A. (1975) Tao: The Watercourse way, Al Huang Pantheon Books, New York – USA, 47-49. PMCid:PMC1130347

Zheng JM, Chin WC, Khijniak E, Khijniak E Jr, Pollack GH (2006) Surfaces and interfacial water: evidence that hydrophilic surfaces have long-range impact. Adv Colloid Interface Sci., 23;127(1):19-27.

Zheng JM, Pollack GH (2003) Long range forces extending from polymer surfaces. Phys Rev E., 68: 031408.

Zheng JM, Wexler A, Pollack GH (2009) Effect of buffers on aqueous solute-exclusions zones around ion-exchange resins. J. Colloid Interface Sci. 332: 511-514.

Zilch L., Maze J., Smith J., Ewing G., Jarrold, M. (2008) Charge separation in the aerodynamic breakup of micrometer-sized water droplets. J. Phys. Chem. A., 112: 13352-13363.

 

Supplementary Material

Field strength Intensities

Auxiliary measurements made during the field investigation regard a Spectran-NF5030 spectrum analyzer (built in EMF-meter). The spectrum analyzer yielded results in the 400 to 600 Hz-range (i.e. 14 V/m near the WF, versus 10 V/m further a field and 8 V/m at 547m distance from the falls = reference site). Unfortunately the instrument used was not able to detect static fields.

In order to complement the field intensities we are able to refer to earlier measurements made during a field-campaign at the Gartl waterfall, together with H. Jell, (Salzburg city council, personal communication, 2005) we know that static field-strength intensities do decrease with distance (see Table S1). The data have been gathered with a set of LF-detectors such as an electric isotropic sensor EFI 3 and a magnetic isotropic sensor MAG 3. The data have been recorded using a data-logger UMS 4 (all units from Fauser Elektrotechnik).

Table S1: Field strength intensities of the Gartl waterfall along a gradient of 100 m.

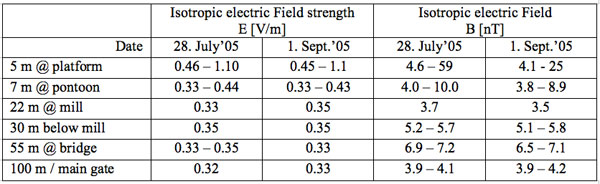
Table S1: Field strength intensities of the Gartl waterfall along a gradient of 100 m.

 

Table S2: Water quality report for water from the Krimml and Stuiben waterfalls (three samples each).


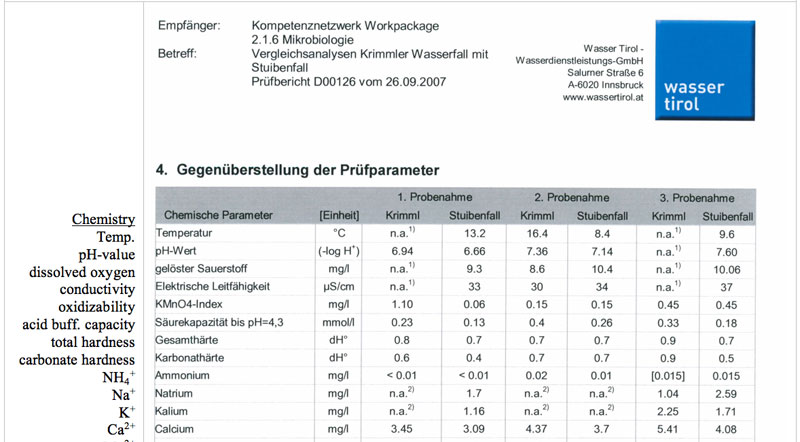
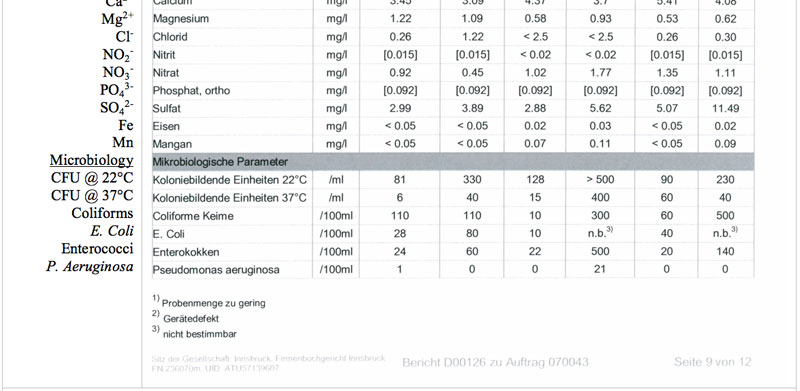
Table S2: Water quality report for water from the Krimml and Stuiben waterfalls (three samples each).

 

Water Analysis

Together with the Alpenverein and the major of Krimml, it was possible to retrieve a water quality report. The analysis dates back to the period between 18th to 31st July 2007 where three samples have been screened at two different waterfalls – the Stuiben and the one at Krimml – the former was not studied in this field investigation. The excerpt in Table S2 depicts a summary and assigns the Krimmler waterfalls top grade (category “A”). The parameters listed below and have been determined according to Austrian Standardization Guidelines.

Close Menu