 Why Is Catalase So Fast? A Preliminary Network Hypothesis for the Rapid Enzyme-catalysed Decomposition of Hydrogen Peroxide
Why Is Catalase So Fast? A Preliminary Network Hypothesis for the Rapid Enzyme-catalysed Decomposition of Hydrogen Peroxide
Lionel R. Milgrom1*
1School of Human Sciences, London Metropolitan University, 166-220 Holloway Road, London N7 8DB, UK
*Correspondence E-mail: [email protected]
Key Words: Catalase; hydrogen peroxide disproportionation; hydrogen-bonded networks; colligative properties; exclusion zones (EZ).
Received May 10th 2015; Revised Oct 12th; Accepted March 1st 2016; Published April 15th; Online April 28th, 2016
Abstract
Catalases are some of the most efficient enzymes known, disproportionating hydrogen peroxide (H2O2) to water and oxygen at rates of around tens of millions of molecules per second. Conventional biochemistry suggests a random diffusion-limited mechanism in which H2O2 molecules make their way from the external aqueous milieu, down channels from the enzyme surface, to the active sites where they are disproportionated at an extremely rapid rate.
Here, an alternative mechanism for the efficiency of catalase action is proposed, which at the same time does not contradict its known enzyme biochemistry. Catalase proteins are envisaged as epicentres of an extended network of hydrogen-bonded water and H2O2 molecules, stretching out from beyond the enzymes’ active sites, into the external cellular aqueous milieu. Consequently, as catalase functions, it provides a coherent oxidative ‘pulse’ to the H-bonded network that effectively ‘unzips’ H2O2 molecules into water and oxygen as far as it extends from the enzyme.
Such a mechanism predicts that most catalase H2O2 disproportionation should be occurring external to the enzyme. An experimental protocol is proposed, using immobilised catalase and the chemiluminescent reagent luminol, which if successful, would suggest (at least as far as catalase is concerned) some re-evaluation of the reductionist framework of enzyme reaction mechanisms involving just random molecular collisions.
Article Outline
- Introduction
- Current Thinking About Catalase
- Is Enzyme Action Due to Random Collisions or Coherent ‘Action-at-a-Distance’?
- A Network Hypothesis for Catalase Action
- Discussion
- Conclusion
- Acknowledgements
- References
Introduction
Preamble: It could be argued that to become more acceptable within mainstream medicine, the complementary and alternative medical (CAM) components of integrative medicine need evidence bases whose rigour matches that of mainstream medicine. Leaving aside the question of whether or not such evidence bases already exist, the problem with such an argument is that it assumes:
• The evidence base for conventional medicine is itself rigorous;
• The reductionist biochemical framework underpinning much of today’s biomedical practice is fundamentally correct. An example of this last point might be the classical view of enzyme catalysis. This is predicated on a reductionist narrative that cellular reactions occur as a result of random thermal molecular motions. Throughout its life therefore, all a cell’s biochemical complexity amounts to is a series of responses to chaotic molecular collisions.
Thus, the catalases constitute some of the most efficient enzyme systems known, with large specificity constants kcat/Km of around 108 to 109 M-1 s-1 [Web reference 1]. This means catalases are capable of disproportionating many tens of millions of hydrogen peroxide (H2O2) molecules per second. In order to achieve such extraordinarily high rates of reactivity, H2O2 molecules would need to travel extremely rapidly to and react with, active sites buried deep within the enzymes’ protein structures, and far removed from the bulk intracellular aqueous milieu in which they function. This might suggest that catalases operate with kinetics that seemingly are impossibly faster than H2O2 diffusion rates. Although several mechanisms have recently been invoked to explain this phenomenon (including spacial and force-field factors between enzyme and substrate [Chou and Jiang, 1974], and quantum mechanical tunnelling [Garcia-Viloca et al., 2004; Olsen et al., 2004; Kamerlin and Warshel, 2010]), it is difficult to fully reconcile the speed, precision, and subtlety of catalases with a classical reductionist narrative of diffusion-controlled random molecular collisions.
In this paper, an alternative hypothesis for catalase efficiency is proposed. This envisages the enzyme acting as a ‘hub’ embedded in, connected to, and acting on an essentially exo-enzymatic hydrogen-bonded network of intracellular water and H2O2 molecules.
Oxygen and evolution: A major breakthrough occurred during the evolution of life on Earth, when organisms acquired the ability to utilise molecular oxygen [Web references 2 and 3]. Among other things, this enabled the aerobic catabolism of foods (oxidative cellular metabolism) which produces far greater amounts of energy than can be obtained anaerobically.
Over billions of years, this led to predation and a gradually accelerating rate of evolution. Increasingly complex animal and plant life forms colonised the planet, culminating in the appearance of mammals about 200 million years ago, and later to the rise of some top mammalian predators after the dinosaur extinction around 66 million years ago. So, “Oxygen is life….Take away oxygen and organisms cannot produce enough energy to support an active lifestyle, or even make them worth eating. Predation, an essential driver of evolutionary change, becomes impossible.” [Lane, 2010]
Living with oxygen: There is however, a potential downside to oxygen: it is all too readily converted into compounds called reactive oxygen species or ROS (sometimes via photosensitised photochemical production of singlet oxygen, 1O2) [Milgrom, 1997; Imlay, 2013]. These include hydroxyl radicals, .OH; nitric oxide, NO; superoxide radicals, O2–., and peroxide, O22- (as hydrogen peroxide, H2O2). Critically, however, small amounts of ROS are necessary for healthy functioning as they are important intercellular signalling molecules: in large amounts though, ROS can be highly toxic because of their ability to react with sensitive intracellular biomolecules (DNA, proteins, lipids in bi-layer membranes, etc.) and so disrupt the vital biochemical pathways that sustain life [Morrell, 2010]. This is called oxidative stress.
A cell’s response to too much oxidative stress is to commit suicide, via the activation of caspases (an acronym derived from their full name, cysteine-aspartic proteases) [Thornbury and Lazebnik, 1998]. They function as so-called ‘executioner’ proteins triggering apoptosis (programmed cell death), necrosis, and inflammation. Though in acute conditions, this is effective in the short term, it is thought that chronically high levels of ROS-induced oxidative stress may cause severe tissue damage, leading to a number of diseases including inflammatory joint disease, insulin-dependent diabetes mellitus, asthma, cardiovascular disease, and many neurodegenerative diseases, e.g., Alzheimer’s and amyotrophic lateral sclerosis (ALS or Lou Gehrig’s disease – a progressive neurodegenerative disorder which affects motor-neuron cells in the brain and the spinal chord, leading ultimately to total paralysis).
Are ROS always bad? This ‘bad-guy’ image [Rhodes, 2011] of ROS however, has been challenged recently with suggestions that ROS are not as toxic as thought [Ahluwalla, et al., 2004], and that they could actually help strengthen an organism by triggering the body’s protective and repair mechanisms [Web reference 4]. In addition, cells are not completely defenceless, as they are able to deploy a range of antioxidant enzymes to counteract ROS (see Figure 1). For example, superoxide dismutases (SODs) convert superoxide O2–. to oxygen and hydrogen peroxide [McCord and Fridovich, 1988], while catalases and glutathione peroxidases disproportionate hydrogen peroxide into harmless water and oxygen gas [Diaz et al., 2012]. Indeed, it is now evident that deficiencies or imbalances in cellular anti-oxidant enzyme levels can result in, or be a signature of cancer cells [Oberley and Oberley, 1997].
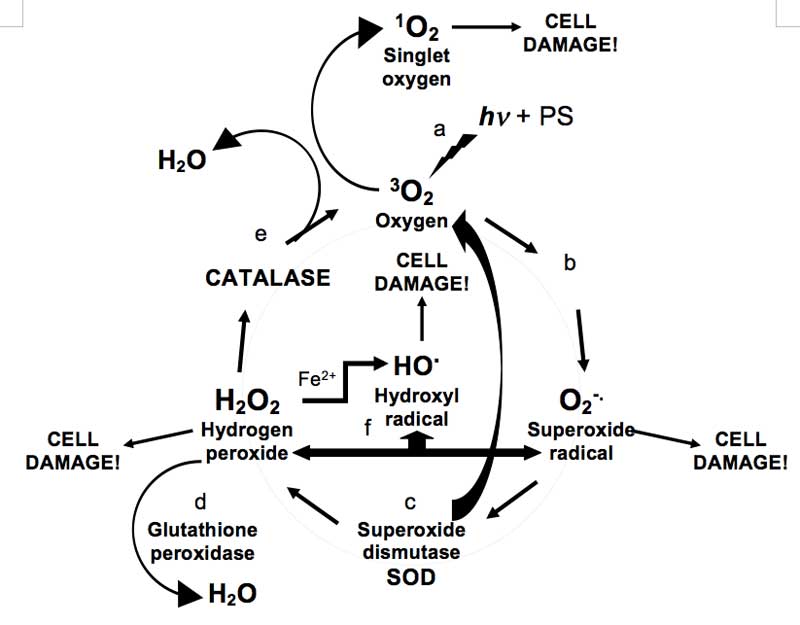
Figure 1: Simplified diagram of ROS production and scavenging: a, Triplet ground-state oxygen 3O2 is photo-sensitised (hv + PS) to highly reactive singlet oxygen 1O2; b, oxygen converted to superoxide radicals; c, SOD converts superoxide radicals to hydrogen peroxide and oxygen; d, glutathione peroxidase converts hydrogen peroxide to water; e, catalase converts hydrogen peroxide to water and oxygen; f, routes for the production of hydroxyl radicals – hydrogen peroxide can react with ferrous ions and superoxide.
Hydroxyl radicals however, represent a ‘chink’ in this anti-oxidant armour. They can be produced in the body from superoxide and hydrogen peroxide (via the Haber-Weiss reaction [Koppenol, 2001]) or by hydrogen peroxide reacting with ferrous Fe2+ ions (via the Fenton reaction [Goldstein et al., 1993]): against hydroxyl radicals there is no enzymic defence [Sies, 1993]. Though hydroxyl radicals are more reactive than superoxide and hydrogen peroxide, their destructive action occurs over a much shorter range. Yet they are thought to be responsible for several neurological autoimmune diseases, e.g., HIV-associated neurocognitive disorders (HAND) that are associated with metabolic encephalopathy induced by HIV infection [Gray et al., 2001].
Nevertheless, without the evolution of superoxide dismutase and catalase antioxidant enzymes, it is doubtful whether oxidative cellular metabolism could have ever been possible. Living with oxygen it would appear, is a precipitous existence involving continuous cellular ‘negotiation’ between the beneficial and harmful aspects of ROS. Eventually, however, this negotiation fails [Rhodes, 2011], as all cells and ultimately the organisms of which they are a part, age and die.
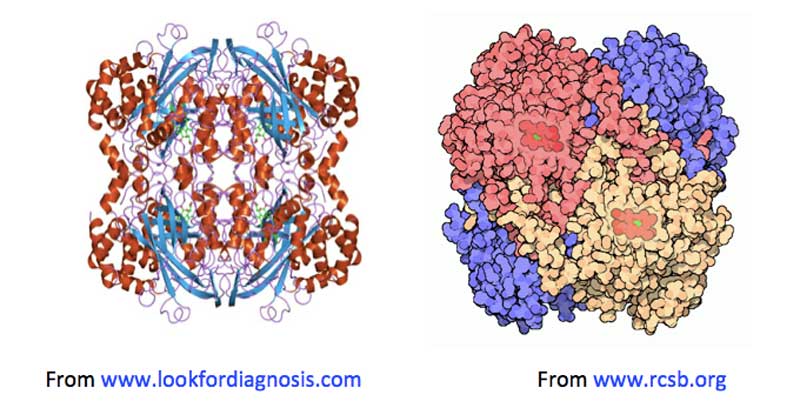
Figure 2: Two images of catalase, both showing haemin units (on the left, in green: on the right in red), buried below the surface of the enzyme, along increasingly narrow channels, lined with hydrophobic amino acids.
The Catalases: Ubiquitous throughout nature, catalases group into three clades: 1, green algae and plants; 2, archaea, bacteria and fungi; 3, archaea, bacteria, fungi, and animals [Klotz and Loewen, 2003; Zamocky et al., 2008]. All catalases oversee the highly efficient conversion of hydrogen peroxide into oxygen and water.
(1) 2H2O2 = 2H2O + O2
Indeed, catalase enzymes are the most efficient, catalysing this disproportionation sometimes up to the staggering rate of many tens of million hydrogen peroxide molecules per second [Rhodes, 2011]. It is worth thinking about this briefly: it means hydrogen peroxide molecules enter catalases’ active sites, react, and the products (oxygen and water) exit the enzyme every tens of millionths of a second.
Most catalases are haemin-containing enzymes (i.e., their active sites consist of a ferric Fe3+ ion complexed within a planar cyclic tetradentate porphyrin ligand [Milgrom, 1997]) made up of tetrameric protein subunits (see Figure 2). Each subunit’s active site is buried deep within the protein structure, and is only accessible from the surface via channels lined with hydrophobic amino acids. It is thought these channels are the routes H2O2 molecules use to find their way from outside the enzyme to the active sites where the disproportionation reaction takes place [Diaz, 2012].
Some catalases are capable of using hydrogen peroxide to catalyse the oxidation of organic compounds, such as alcohol. Such enzymes are said to be bi-functional having both catalase and peroxidase activity [Web reference 2]. There are also bacterial catalases whose action depends not on haemin but instead utilise complexes of manganese ions. Here, only mono-functional, haemin containing catalases are considered.
As proteins go, catalases are slightly tougher than most, having relatively stable structures that are better able to resist pH changes, thermal denaturation and proteolysis than other enzymes [Web reference 2]. This greater stability is important during times in a cell’s life-cycle when levels of proteases are high and there is rapid turn over of protein. Given their central role in maintaining the viability and health of aerobic organisms, it would be advantageous to further understanding the aetiology and progress of some of the chronic diseases mentioned above, if we could fully comprehend how catalases work.
Although much is known about the structure of catalases [Diaz, 2012] and the overall mechanism [Dominguez, 2010] by which they disproportionate H2O2, how they do it so efficiently is not entirely understood. In particular, the incredibly high throughput of H2O2 molecules from outside the enzyme deep into its active-site interior, and water/oxygen egress post reaction, would all seem to militate against the notion of an essentially random, iterative, molecule-by-molecule H2O2 disproportionation reaction mechanism.
Consequently, while in agreement with many years of biochemical findings, the model for catalase action suggested here will attempt to augment current thinking about its mechanism. It proposes catalases serve as ‘hubs’ for an extremely fast ‘network’ of coordinated H2O2 dis-proportionation reactions which, though triggered by and from the enzymes’ active sites, would occur mainly some distance away, in the bulk of the surrounding fluid medium.
Current Thinking About Catalase
The catalase H2O2 disproportionation reaction: As mentioned earlier, catalase enzymes are the most efficient, capable of disproportionating many millions of H2O2 molecules per second. The accepted mechanism of this catalytic reaction (derived from many years of biochemical and modelling studies) envisages a two-step process shown in Equations 2 and 3 [Alfonso-Prieto, 2008]. Here, ‘Enz-[Por-Fe(III)]’ represents the resting state of the enzyme ([Por-Fe(III)] being the Fe3+ porphyrin active site). This undergoes two-electron oxidation (and oxygen transfer) by an H2O2 molecule to an oxyferryl porphyrin π-cation radical active form of the enzyme (known as Compound 1), represented by ‘Enz-[Por+.-Fe(IV)=O]’ in Equation 2. The H2O2 molecule is reduced to water. Then, in what has come to be known as the catalatic step [Diaz, 2012], Compound 1 is reduced back to the resting state of the enzyme by another H2O2 molecule, which is itself oxidised to water and oxygen in Equation 3. The sum total of these reactions (adding together Equation 2 and 3) simplifies to the disproportionation reaction shown in Equation 1.
(2) Enz-[Por-Fe(III)] + H2O2 = Enz-[Por+.-Fe(IV)=O] + H2O
(3) Enz-[Por+.-Fe(IV)=O] + H2O2 = Enz-[Por-Fe(III)] + H2O + O2
Adding Equations 2 and 3:
(1) 2H2O2 = 2H2O + O2
As a haemin-containing enzyme, bovine liver catalase (BLC) was one of the first proteins to be crystallised [Sumner, 1937] in 1937, but its high-resolution crystal structure (and those of catalases from other organisms) was not solved until more than 40 years later [Murthy, 1981; Reid, 1981; Vainshtein, 1981; Foroughi, 2011]. Ultimately, what these crystal structures of monofunctional catalases reveal is that they consist of four tightly integrated protein subunits, each of around 55 to 69 kDa for clades 1 and 3 catalases (i.e., small-subunit catalases or SSCs such as BLC), and around 75 to 86 kDa from clade 2 (i.e., large-subunit catalases or LSCs). In all haemin-containing catalases, their active sites are buried deep inside each sub-unit around 20 Å beneath the catalase molecular surface.
Detailed analysis of these crystal structures combined with molecular dynamics studies reveal that there are channels (the main ones around 40-45 Å long) leading from the catalase surface to the active sites [Dominguez, 2010; Kalko, 2001]. In clade 2 LSCs (but not clade 1 and 3 SSCs), these main channels are interrupted by a ‘gate’ consisting of a short peptide loop of four amino acids (the purpose and significance of this gate will be discussed later).
Further, the amino acids on the surface of catalase and leading down into these channels to the active sites (mainly histidine, proline and charged residues) are so arranged that the relative proportion of H2O2 to water molecules gradually increases, from the bulk phase around the enzyme to close to the catalase surface (about 4-5 Å), to the active sites. Thus it appears that the amino acid sequence of catalase enzymes have evolved in such a way as to ensure that in an aqueous milieu containing H2O2, it is the latter that is gradually concentrated at the active sites, and that this helps account for these enzymes catalytic efficiency [Dominguez, 2010].
Further insights into catalase structure: As mentioned above, only LSCs from clade 2 possess the short tetrapeptide ‘gate’ interrupting the main channel from the surface of catalase down to the enzyme’s active sites. It has been suggested that the function of this gate is to control access of H2O2 to the haemin active sites [Dominguez, 2010].
Thus Compound 1 (containing the highly reactive oxyferryl intermediate shown in equation 2) if not immediately involved in the disproportionation step of Equation 3, can go on to inactivate the enzyme. So, it is reasoned, an important function of the tetrapeptide ‘gate’ “..would be to regulate access of H2O2to the active site in such a manner that Compound 1 is only formed when a second molecule of H2O2 is present to complete the reaction.” [Dominguez, 2010] Gate opening would therefore be dependent on H2O2 concentration at the accesses to the gate (molecular modelling shows that at 6M H2O2 concentration, all the gates would be open, but that at ~300 mM H2O2 concentration, only half the gates would be open), which could help explain the observation that catalase enzyme activity increases with H2O2 concentration [Diaz, 2001; Diaz, 2009].
The absence of such gating in front of the active sites for SSCs, particularly for clade 3 catalases (which includes multicellular animals) might suggest that H2O2 production levels in the intracellular milieu of faster metabolising creatures are large enough to ensure enough H2O2 molecules will always reach the active site in time to react with the Compound 1 intermediate before it can inactivate the enzyme.
To sum up, catalases:
1. Are ubiquitous throughout nature in aerobic organisms as one of the frontline defences against ROS, particularly H2O2;
2. Are among the most efficient enzymes, turning over many millions of H2O2 molecules every second;
3. Have active sites buried deep within their protein structures;
4. Have groupings of amino-acid residues in their tertiary protein structures which have the effect of concentrating H2O2 molecules near and into the channels leading down to their active sites;
5. The H2O2 disproportionation reaction (Equation 1) requires two molecules of H2O2 so that the first-formed highly active intermediate compound 1 does not survive long enough to inactivate the enzyme.
6. To achieve this, LSCs (but not SSCs) have short tetrapeptide ‘gates’ which block access to their active sites until the H2O2 concentration is large enough.
It is thought the last three points are the reasons for the efficiency of catalases. This, in turn, rests on the assumption that the catalase disproportionation reaction occurs via an extremely rapid but sequential iteration of H2O2 molecules through the enzyme’s active sites.
Here an additional possibility is considered. In aqueous solution, H2O2 is known to form strong hydrogen bonds in water [Moin, et al., 2012], so that within the aqueous milieu of aerobic organisms’ intracellular fluid, H2O2 can form a network of dynamically hydrogen-bonded molecules [Web reference 5]. Therefore, catalase enzymes would be sitting within (and connected via their active sites to) this hydrogen-bonded network. It is proposed therefore, that catalases might well be able to catalyse the ultra-fast disproportionation of H2O2 outside the enzyme in the intra-cellular aqueous milieu, via a coherent mechanism.
Is Enzyme Action Due to Random Collisions or Coherent ‘Action-at-a-Distance’?
The standard model for enzyme action: This involves an essentially two-step process in which a substrate S binds reversibly with the enzyme E to form an enzyme-substrate complex ES (Equation 4). Formation of this complex has the effect of stabilising the substrate’s transition state of the reaction. This (with the aid of co-factors and/or metal ions) then goes on to form the product irreversibly (Equation 5), and on its release from the enzyme, leaves the latter ready to repeat the process.
(4) E + S ⇆ ES
(5) ES = E + P
Why the substrate S would be bound selectively into the enzyme’s active site is explained in terms of the well-known ‘lock and key’ principle (and its updated induced-fit modification) [Kent, 2000]. Here, certain amino-acid side-chains in the active site (specifically, their respective chemical properties), combined with the enzyme’s shape, lead to only one or at most a few types of molecules that can bind long enough for an irreversible chemical reaction to take place. Thus most enzymes exhibit a high degree of specificity; binding specific substrates, catalysing specific reactions usually extremely rapidly, and producing specific products. The problems arise when it comes to accounting for this behaviour within a reductionist paradigm of conventional biochemistry.
“…full of sound and fury, signifying nothing…”[Shakespeare, 1623] or meaningful response? Watterson discusses in detail the differences between what he calls the classical or traditional (reductionist) view and the structuralist view of the energetics of living processes [Web reference 6]. Thus in the classical view cellular reactions are merely responses to the thermally driven random collisions of molecules: metabolic pathways are nothing other than sequences of independent reactions occurring as if all the reagents were present in solution. “The cell itself is a complicated, but nonetheless statistical, collection of chemicals, and its behaviour at any moment is an average behaviour.” [Web reference 6] In other words, however sophisticated, the cell is just a random “bag of chemicals” [Dawkins, 1988].
In the structuralist view, stimuli (chemical messengers) initiate responses in the form of chemical reactions, which occur in a strict sequence that can spread coherently across the whole cell. In this way, the cell’s response may be interpreted as being ‘meaningful’. As a consequence, the cell’s energy resources are not randomly squandered, but stored and manipulated in a way reminiscent of information processing. Thus the structuralist view is of “..the cell as a unit, in which the internal processes are under its control, in contrast to one of a chaotic collection of chemical reactions.” [Web reference 6]. It is in considering the nature of these energy resources that the reductionist view of cellular reactions could be in difficulties.
The problem with proteins: For example, proteins are relatively easily denatured in aqueous solution, which means that the stability of their all-important shapes is low; in the range of 20 – 60 kJ mol-1 [Kauzmann, 1959; Tanford, 1968]. Hydrogen-bond energies are of the order of 12 – 38 kJ mol-1 [Fersht, 1999]. As Watterson points out [Web reference 6], this can only mean that protein molecules consisting of several thousand chemically bonded atoms, rely on just a few relatively weak (when compared to covalent bonds) hydrogen bonds to hold them together [Finney, 1982]. In other words, given how relatively low these energies are, it is surprising proteins are able to retain their 3-D shapes (vital to their functions) within the energetic cellular environment; something the classical reductionist view of cellular reactions is unable to predict or explain b. Enzyme catalysis emphasises this point.
bWatterson’s “wave-cluster-domain model” attempts to integrate the active cooperation and participation of cellular water with the action of a cell’s biomolecular components [Watterson, 1991; Watson, 1995]
Here, the reductionist view maintains that the energy released from enzyme-substrate binding is used to lower the activation energy of the transition state. Though this energy (on moderate binding affinity) amounts to around only 30 kJ mol-1, i.e., that of just a few hydrogen bonds, if it were retained by the enzyme and not dissipated, it would still be enough to denature the protein (the slightly greater stability of catalases mentioned earlier, not withstanding). Quoting Watterson, “…it is doubtful that nature evolved catalytic machines which are on the verge of breakdown each time they begin to function…” [Web reference 6].
Further, as they function, proteins may undergo large conformational changes, which in the classic view, are envisaged as occurring in empty space. Again, Watterson points out that this ignores the effect of the intracellular cytoplasmic aqueous milieu in which these changes take place, and which has the same density and thermal energy as its protein solute [Web reference 6]. In this situation, the protein’s hydrophilic domains have many thousands of water molecules associated with them. Their mobilisation requires large numbers of solvent hydrogen bonds to be broken, and whose collective energy far exceeds the thermal stability of the protein’s hydrophilic domains.
For example, at a very conservative ‘guestimate’ (taking the lowest of the range of hydrogen bond energies above – 12 kJ/mole – and just a thousand water molecules associated with a protein’s hydrophilic domains), one arrives at a figure of around 12,000 kJ/mole for their collective energy (assuming each water molecule forms just one hydrogen bond with a neighbour or the protein: a water molecule can form up to four hydrogen bonds with its neighbours [Jorgensen and Madura, 1985]). This is roughly equivalent to the energy of over thirty carbon-carbon, carbon-nitrogen, or carbon-oxygen covalent bonds [Jones and Atkins, 2000], in other words, more than enough energy to not only disrupt protein folding, but to potentially begin breaking apart a protein’s primary structure. Thus the aqueous cytoplasmic surroundings ought to be having a major disruptive effect on protein function [Watterson, 1997]. Yet clearly it does not, because proteins retain their shape and function.
Consequently, while the reductionist classical view might be valid for describing ordinary solution chemistry performed in laboratory glassware (the surrounding solvent acting as a ‘heat bath’ for the reactants), it is inadequate when considering protein structure and function within the cellular cytoplasm: for there is nothing random, chaotic, or statistical about cellular biochemical events. Such predetermination of reaction sequences must involve active cooperation between the water of the cytoplasmic medium, with proteins, DNA, lipids, and other cellular biomolecules. This means “…cellular processes involve energies far in excess of those supplied by metabolic steps like substrate binding.” [Web reference 6]
Colligative properties: Watterson [Watterson, 1996] and Chaplin [Chaplin, 2012] suggest the source of this energy might originate from within the colligative properties of water c, via the opposing forces of pressure at the macro level (e.g., of the ‘container’, in this case, the cell membrane), and attractive intermolecular forces (e.g., hydrogen bonding, London dispersion forces, etc.) between molecules, on the micro level. This could lead to some dynamic ordering of the solvent into flexible giant short-lived 3-D clusters, that could perhaps provide just the kind of mesoscopic [Subramanian and Anisimov, 2014] environment to support a sequence of predetermined cellular reactions (see Figure 3)
cThose properties (e.g., elevation and depression of freezing point, relative lowering of vapour pressure, and osmotic pressure) that depend on the ratio of solute particles to solvent molecules, and which are independent of the nature of the solute.
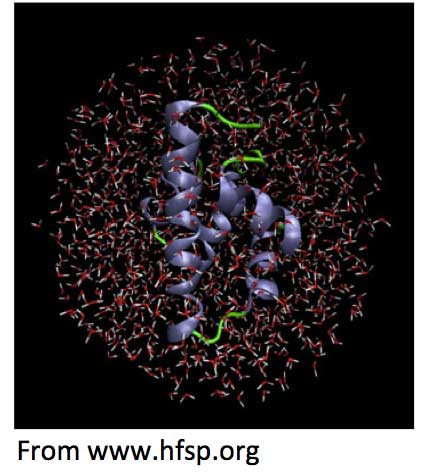
Figure 3: A protein molecule surrounded by a mesoscopic sphere of water molecules
Variations in the number of dissolved solute molecules (e.g., proteins) in a solvent can lead to the generation of high osmotic pressures at aqueous interfaces [Chaplin, 2014], particularly ion-exchange and uncharged hydrophilic surfaces. Indeed, large osmotic pressures can also be generated at hydrophilic surfaces without any solvent [Chaplin, 2012]. Consequently, far from envisaging the cell’s biomolecular reactions as occurring randomly in a vacuum, they proceed against an ordered backdrop of active cytoplasmic aqueous involvement. This is constantly pushing, pulling, extending, contracting, flowing or gelling, so providing an energy operating above the level of thermal collisions and which can override their disruptive effects.
…. And exclusion zones: A somewhat alternative view for the origin of a potential source of cellular energy has been proposed by Pollack et al. [Pollack, 2013a] and others [Mollenhauer and Morre, 1978; Green and Otori, 1970; Yoshida, et al., 1995], concerning the mesoscopic d properties of aqueous solutions next to surfaces [Chai et al., 2008; Zheng et al., 2006; Chai et al., 2012; Sulbaran, 2014]. It appears that interfacial water next to ionically charged or neutral uncharged hydrophilic surfaces expels solutes into the bulk of the solution. This creates an “exclusion zone” (EZ) free of solute particles, that can extend some several hundred microns back from the surface. Moreover, it can be visualised [Pollack, 2013a] using low molecular weight dyes, proteins, and microspheres. Indeed, the existence of force fields in the EZ has been demonstrated, which reduce in strength as a function of distance from the surface [Chen et al., 2012; Huszar et al., 2014].
dMesoscopic = a particle size regime midway between microscopic and macroscopic, characterised by regions where large numbers of particles are quantum mechanically correlated with each other.
The water in the EZ has some interesting properties. Thus, it has an absorption peak at 270 nm, greater density, greater viscosity, a negative charge compared with bulk water, and the ability to store energy; enough energy, it would seem, to drive biological reactions. Pollack has explained these findings [Pollack, 2013a] based on the notion of the EZ layer being in a different state to liquid water, more akin to a liquid crystalline (or fourth) phase of water, based on a honeycomb structure consisting of repeating giant 2—D hexagonal layers (see Figure 4). This has been dismissed by Chaplin [Chaplin, 2012] partly on the grounds that generation of osmotic pressure at aqueous interfaces might be a better explanation, and abhorrence of Pollack’s use of the idea of 2-D hexagonal water clusters to explain his findings (this first appeared during the abortive debate over “polywater” more than forty years ago [Web reference 7], which was later debunked [Rousseau and Porto, 1970]).
Pollack’s ideas have also been criticised (from within his own Department of Bioengineering at the University of Washington in Seattle, USA) and an alternative explanation was put forward in terms of concentration gradients [Schurr et al., 2013; Schurr, 2013]. This, in turn has been refuted and answered by Pollack [Pollack, 2013b]; osmosis and the formation of electrical gradients being seen as secondary to EZ formation at interfaces and around solute particles.
It is not the purpose of this paper to compare and contrast these various views on the possible generation of cellular energy. Rather it is to use them to indicate that the classical reductionist view of how cellular biochemistry works seems inadequate for the task of dealing with certain inescapable energetic facts, and that there are better more systems-oriented interpretations worthy of pursuit. Finally in this section we shall examine some recent data, which suggests that proteins and their substrates might not need to be in direct contact for biochemical reactions to take place.
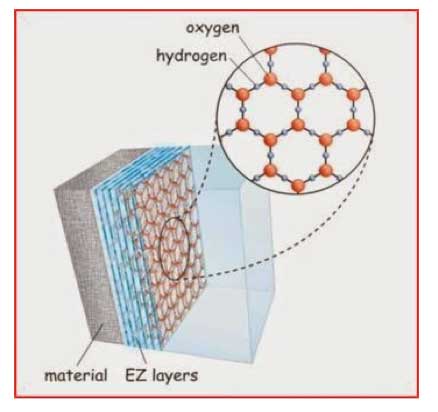
Figure 4: Layers of EZ (exclusion zone) water next to hydrophilic material.
The sense of smell: All molecules possess their own shapes, and the more atoms there are in a molecule, the more complex those shapes can become. It has generally been thought that a molecule’s shape determines what it will smell like. This is based on the traditional ‘lock-and-key’ principle (similar to that used to describe how enzymes catalyse reactions with their substrates) in which protein-based receptors in our noses match certain molecular shapes [Gaillard et al., 2004]. Generally, when the right shaped molecule fits into the right receptor, a signal is triggered in an attached neurone, which then transmits the signal to the part of the brain where olfaction is perceived.
Recent research however suggests that the simple lock-and-key principle on which the olfactory properties of molecules are supposed to be based, might not be entirely correct. Thus, if all the hydrogen atoms in the molecule acetophenone (see Figure 5a) are replaced with hydrogen’s heavier isotope deuterium, Turin et al. were able to demonstrate that the resulting deuterated acetophenone (see Figure 5b) was perceived to smell differently [Gane et al., 2013]. The two molecules have the same shape and only differ in that all their C-H bonds are replaced by C-D bonds.
The essential difference between these two molecules therefore is not in their shapes or sizes, but in their C-H and C-D vibrational frequencies. Turin suggests perhaps our sense of smell depends on sensing differences in vibrational frequencies, not necessarily differences in molecular shape and size. Now, this is a quantum mechanical effect, which is transmitted through space and would not require molecules to first be in direct physical contact with their protein receptors.
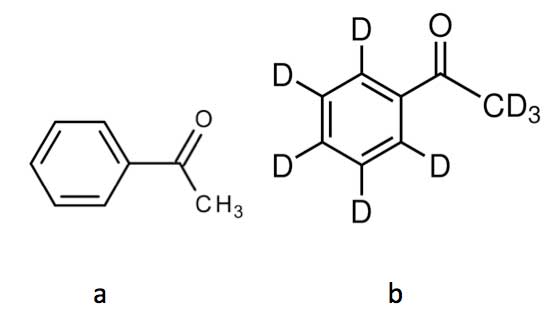
Figure 5: Acetophenone (a) and deuterated acetophenone (b).
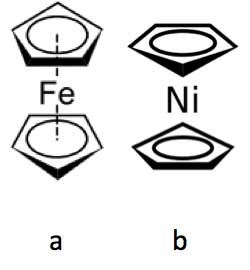
Figure 6: Ferrocene (a) and nickelocene (b).
Brookes et al. have noted a similar olfactory difference between the molecules ferrocene, which has a spicy smell (see Figure 6a), and nickelocene, which smells oily (see Figure 6b). Both molecules have the same shape and size but differ only in their central metal atom (iron in ferrocene and the only slightly heavier nickel in nickelocene) [Brookes et al., 2012]. Again, this means there will be key molecular vibrational differences between them, which presumably accounts for their olfactory differences.
However, a much more striking demonstration of the importance of molecular vibrations in olfaction is when two entirely differently shaped and sized molecules are perceived as having similar smells. Thus the small triatomic V-shaped molecule hydrogen sulphide (H2S; Figure 7a) has a similar smell of rotten eggs as the much more complex decaborane (B10H14; Figure 7b), which consists of a cluster of ten boron and fourteen hydrogen atoms arranged in an open basket shape [Brookes et al., 2012]. Surprisingly, the two molecules appear to have similar overall vibrational frequencies, and though their sizes and shapes are entirely different, the olfactory receptor site seems to respond to them as if they are the same.
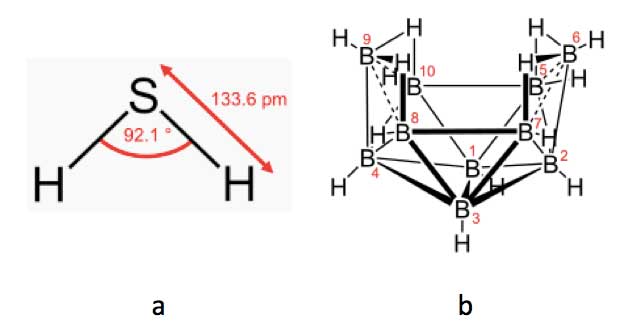
Figure 7: Hydrogen sulphide, H2S (left), and decaborane, B10H14 (right)
It is worth noting that in 1999, the late French biochemist Jacques Benveniste announced similar conclusions in which he claimed he could record these overall substrate vibrational frequencies, then ‘play’ them back to their receptors, which then responded as if they were in their substrates’ physical presences [Thomas et al. 2000; Milgrom, 2001]. In other words, Benveniste was claiming that receptors could react at a distance electromagnetically to the overall vibrational signatures of their substrates, and not necessarily just to their direct physical presence. Although the results of Benveniste’s so-called ‘digital biology’ experiments were later attributed to an experimenter effect [Jonas et al. 2006] (and so in many people’s minds, effectively debunked), along with the work of Turin and Brookes (and all that has been mentioned in this section so), it would suggest the classic lock-and-key hypothesis for enzyme/receptor-substrate interaction is inadequate.
A Network Hypothesis for Catalase Action
The formation of giant hydrogen-bonded water clusters in a wide-range of concentrations and thermodynamic conditions has been studied for some time [Geiger et al. 1979; Partay et al. 2007], both experimentally and theoretically using percolation theory [Stauffer, 1985]. In the latter, a percolation threshold is defined which pertains to the formation of long-range connectivity in random systems, below which a giant connected component does not exist.
For the purposes of the hypothesis to be developed here, we may assume that the aqueous milieu of the cellular cytoplasm is in a state above the percolation threshold, so that a giant hydrogen-bonded network exists within it. From this perspective, it is worth remembering that hydrogen peroxide forms strong hydrogen bonds with water [Moin, 2012], which would give added impetus to the notion that catalase operates within an intracellular hydrogen-bonded network.
As before, we represent the resting state of the enzyme as Enz-[Por-Fe(III)], and the active state oxo-ferryl Compound 1 as Enz-[Por+.-Fe(IV)=O]. The catalase enzyme is now envisaged as a ‘hub’ sitting in a network of hydrogen-bonded water and H2O2 molecules which is connected via the channels leading from the surface, to the enzyme’s active sites. This means that instead of considering the H2O2 molecules as being presented individually and in rapid succession to the active sites, it is necessary to consider the whole network of nH2O2 molecules hydrogen bonded to water and each other, spreading out from the enzyme.
The H2O2 molecule closest to the active site oxidises the resting enzyme to Compound 1, and is itself reduced to water. However, this leaves (n-1)H2O2 molecules still networked. The active Compound 1 then oxidises a H2O2 molecule to water and oxygen in the so-called catalatic step but, it being connected to the rest of the network, causes the latter to effectively ‘unzip’ other H2O2 molecules, the whole network undergoing a fast coherent reaction to water and oxygen. The sequence of reactions may be formulated as follows:
(6) Enz-[Por-Fe(III)] + nH2O2 = Enz-[Por+.-Fe(IV)=O] + H2O + (n-1)H2O2
(7) Enz-[Por+.-Fe(IV)=O] + (n-1)H2O2 = Enz-[Por-Fe(III)] + H2O + O2 + (n-2)H2O + (n-2/2)O2
Adding Equations 6 and 7 gives:
(8) nH2O2 = 2H2O + O2 + (n-2)H2O + (n-2/2)O2
Which simplifies to:
(9) nH2O2 = nH2O + n/2 O2
Finally, doubling both sides of Equation 9 and dividing through by n, gives Equation 1:
(1) 2H2O2 = 2H2O + O2
By these reactions effectively reducing back to Equation 1, it implies this preliminary network hypothesis presented here does not contradict the known catalase H2O2 – disproportionation chemistry that has previously been discovered and investigated.
Discussion
This preliminary network hypothesis to explain why catalase disproportionates H2O2 so efficiently is not in itself new. Prior to the lock-and-key [Stryer et al. 2002] and induced fit models [Koshland, 1958], early ideas of enzyme action imagined they induced changes in the surrounding water, which then accelerated reactions in molecules nearby [Kohler, 1973]. Interestingly, this notion of essentially coherent operation has recently been suggested to explain the enzymatic action of endonucleases when reading DNA sequences [Kurian, 2014].
In the case of catalase, it should be remembered that some of its surface amino acids are hydrophilic polar/charged. It is thought this helps concentrate H2O2 molecules near and into the channels leading to the enzyme’s active sites [Dominguez, 2010]. But as Pollack has pointed out, these are also the conditions that could generate EZ layers near the catalase enzyme’s surface [Pollack, 2013a]. EZ layer formation also leads to the generation of free protons (as hydroxonium ions, and less frequently, solvated hydroxide ions), both of which in the presence of transition metal ions such as Fe(II)/Fe(III), are known to provide catalytic environments for H2O2 redox chemistry [Web ref. 8]. Consequently, and in the words of Pollack, “ …biological catalysis may resemble generic catalysis, involving little more than high concentrations of EZ-generated protons.”
Therefore, given that according to Equations 6-9 and 1 the network hypothesis does not appear to violate known chemistry and biochemistry, the notion that catalase activity during H2O2 disproportionation might also be occurring in the cytoplasmic aqueous milieu, does not seem too far-fetched. The question now is how to demonstrate it experimentally.
One possibility as to how this might be achieved is to use the well-known chemiluminescence reaction of H2O2-derived oxygen with luminol [Huntress et al. 1934]. In crime-scene forensics, luminol is used to detect the presence of blood; the iron in the haemoglobin leading to disproportionation of H2O2, whose oxygen release generates luminol chemiluminescence [James and Eckert 1998] (see Figure 8).
To observe exo-enzymatic H2O2 disproportionation, it would however be necessary to use immobilised catalase [Yoon et al. 2007] and then ensure the H2O2-reaction solution containing the luminol underwent the minimum of disturbance. This is to make sure that H2O2 disproportionation really is occurring at a distance from the immobilised enzyme and is not being carried away from it by random mixing of the solution that would occur were the solution to be disturbed.
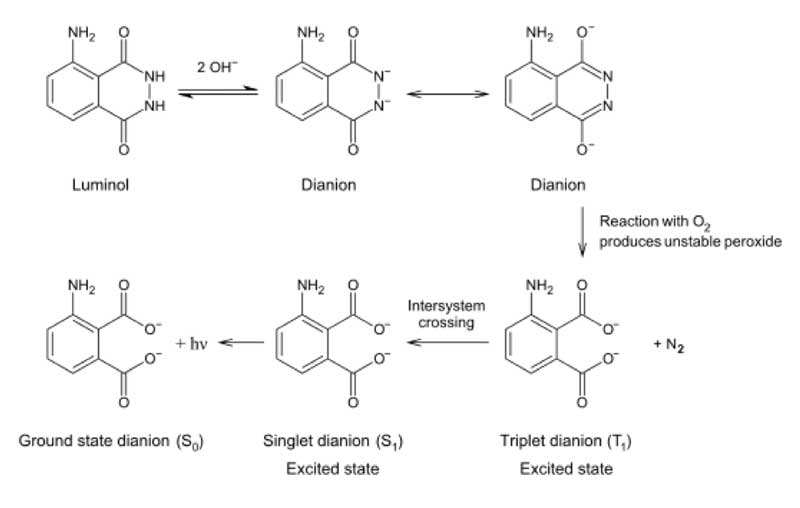
Figure 8: Reaction scheme showing the generation of chemiluminescence when luminol reacts with oxygen.
Conclusion
Proponents of integrative medicine have been criticised for attempting to combine the scientific evidence base of conventional medicine with (it is claimed [Gorski, 2011]) non-science-based complementary and alternative medical (CAM) practices. Apart from a perhaps scientifically imperialistic view [Dupré, 1994] that disregards hundreds of years of practical (so-called ‘anecdotal’) experience, the problems with such criticisms are three-fold.
Firstly, there is either ignorance, or outright rejection of the growing evidence bases for many CAMs [Web references 9 and 10], particularly if they are perceived to contradict the dominant reductionist paradigm of the biosciences. Secondly, the evidence-based medicine ‘brand’ [Greenhalgh, 2014] has itself been accused of lacking relevance to patients, but more seriously has become tarnished by the essentially criminal activities of the globalised pharmaceutical industry [Goldacre, 2012; Gøtzshe, 2013; Kassirer, 2007]. Thirdly, there are fundamental philosophical and practical flaws in the current evidence base of conventional medicine [Milgrom, 2014] which, when combined with an uncritical acceptance of reductionist biochemistry (as taught in many of the standard texts on the subject), can have a negative effect on the introduction of new ideas into the teaching and understanding of biomedicine [Web reference 11].
Thus, as was pointed out earlier, there are anomalies in the classical reductionist interpretation of enzyme activity which when examined more closely, suggest for example that the energies released on substrate binding might be enough to denature the enzyme’s protein. Such a contradiction leads one to suspect that something is missing from the classic interpretation. This might be inclusion of the effect of the cytoplasmic aqueous surroundings (on enzyme activity in particular, and cellular biochemistry in general), in stabilising protein structures. It is within this context that the mechanism of catalase action is being re-evaluated.
Drawing on recent research, the purpose of this paper has been to propose a plausible but at this point still preliminary network hypothesis, as an alternative explanation for the extremely efficient disproportionation of H2O2 by catalase. In so doing, it is hoped that a more systems-oriented, less reductionist approach to the functioning of an important enzyme might help encourage a similar approach to researching and understanding what effects CAM therapies are having at the biochemical level. At this time, however, such speculation must wait until it can be experimentally demonstrated that a network hypothesis of catalase action is not only plausible, but possible. Such experimentation will be reported on in a forthcoming publication.
Acknowledgements
The author is indebted to some of the 6th Form students of University College School, Hampstead, London UK for asking a series of questions which provided the inspiration behind this paper.
References
Ahluwalla J, Tinker A, Clapp LH, Duchen MR, Abramov AY, Pope S, Nobles M, Segal AW (2004). The large-conductance Ca2+-activated K+ channel is essential for innate immunity. Nature 427: 853-7.
Alfonso-Prieto M, Vidossich P, Rodriguez-Fortea A, Carpena X, Fita I, Loewen P, Rovira C (2008). Electronic state of the molecular oxygen released by catalase. J Phys Chem 112: 12842-12848.
Brookes JC, Horsfield AP, Stoneham AM (2012). The swipe-card model of odorant recognition. Sensors 12(11): 15709-49.
Chai B, Zheng J, Zhao Q, Pollack GH (2008). Spectroscopic studies of solutes in aqueous solution. J Phys Chem A 112: 2242-2247.
Chai B, Mahtani AG, Pollack GH. Unexpected presence of solute-free zones at metal-water interfaces (2012). Contemp Mater 3: 1-12.
Chaplin MF (2014). Interfacial osmostic pressure. In: Aqua Incognita: Why Ice Floats On Water and Galileo 400 Years On, pp 329-340. Eds. Lo Nostro P, Ninham BW. Connor Court, Ballarat.
Chaplin MF (2012). Self-generation of colligative properties at hydrophilic surfaces. arXiv:1203.0206 [cond-mat.soft]
Chen C-S, Chung W-J, Hsu IC, Wu C-M, Chin WC (2012). Force-field measurement within the exclusion zone of water. J Biol Phys 38: 113-120.
Chou K-C, Jiang S-P (1974). Studies on the rate of diffusion-controlled reactions of enzymes. Spatial factor and force-field factor. Scientia Sinica 27(5): 664-680.
Dawkins R (1988). The Blind Watchmaker. Penguin Books, London United Kingdom.
Diaz A, Loewen PC, Fita I, Carpena X (2012). Thirty years of heme catalases structural biology. Arch Biochem Biophys 525: 102-110.
Diaz A, Rangel P, Montes de Oca Y, Lledas F, Hansberg W (2001). Molecular and kinetic study of catalase-1, a durable large catalase of Neurospora crassa. Free Radic Biol Med 31: 1323-1333.
Diaz A, Valdes VJ, Rudino-Pinera, Horjales E, Hansberg W (2009). Structure—function relationships in fungal large subunit catalases. J Mol Biol 386: 218-232.
Dominguez L, Sosa-Peinado A, Hansberg W (2010). Catalase evolved to concentrate H2O2 at its active site. Arch Biochem Biophys 500: 82-91.
Dupré, J (1994). Against Scientific Imperialism. PSA: Proceedings of the Biennial Meeting of the Philosophy of Science Association: 374–381.
Fersht A (1999). Structure and Mechanism in Protein Science. Freeman and Co, New York, p179.
Finney JL (1982). Solvent effects in biomolecular processes. In : Biophysics of water, pp55-58. Eds. Franks F, Mathias S. J Wiley and Sons, New York.
Foroughi LM, Kang YN, Matzger AJ (2011). 60 years from discovery to solution: crystal structure of catalase form III. Acta Crystallogr D: Biol Crystallogr 67: 756-762.
Gaillard I, Rouquier S, Giorgi D. Olfactory receptors (2004). Cell Mol Life Sci 61(4): 456-469.
Gane S, Georganakis D, Maniati K, Vamvakias M, Ragoussis N, Skoulakis EM, Turin L (2013). Molecular vibration-sensing component in human olfaction. PLoS One 8(1): e55780.
Garcia-Viloca M, Gao J, Karplus M, Truhar DG (2004). Quantum mechanical methods for biomolecular simulations. Science 303(5655): 186-195.
Geiger A, Stillinger FH, Rahman A (1979). Aspects of the percolation process for hydrogen-bond networks in water. J Chem Phys 70(9): 4185-4193.
Goldacre B (2012). Bad Pharma: How Drug Companies Mislead Doctors and Harm Patients. Fourth Estate, London UK.
Goldstein S, Meyerstein D, and Czapski G (1993). The Fenton reagents. Free Rad Biol and Med 15(4): 435–445.
Gorski D (2011). Andrew Weil and ‘integrative medicine’: The ultimate triumph of quackery? Science-based Medicine, 11th of September.
Gøtzche PC (2013). Deadly Medicines and Organised Crime: How Big Pharma Has Corrupted Healthcare. Radcliffe Publishers, London UK.
Gray F, Adle-Biassette H, Chretian F, Lorin de la Grandmaison G, Force G, Keohane C (2001). Neuropathology and neurodegeneration in human immunodeficiency virus infection. Pathogenisis of HIV-induced lesions of the brain, correlations with HIV disorders and modifications according to treatments. Clin Neuropathol 20(4): 146-155.
Green K, Otori T (1970). Direct measurement of membrane unstirred layers. J Physiol 207: 93-102.
Greenhalgh T. Howick J, Maskrey N (2014). Evidence-based medicine: a movement in crisis? BMJ 327: g3725.
Huntress EH, Stanley LN, Parker AS (1934). The oxidation of 3-aminophthalhydrazide (luminol) as a lecture demonstration of chemiluminescence. J Chem Ed 11(3): 142-145.
Huszar IN, Martonfalvi Z, Laki AJ, Ivar K, Kellermayer M (2014). Exclusion zone dynamics explored with microfluidics and optical tweezers. Entropy 16: 4322-4337.
Imlay JA (2013). The molecular mechanisms and physiological consequences of oxidative stress: lessons from a model bacterium. Nature Reviews: Microbiology 11: 443-454.
James SH, Eckert WG (1998). Interpretation of Bloodstain Evidence at Crime Scenes, p 154. 2nd ed, CRC Press LLC, Boca Raton, Florida.
Jonas WB, Ives JA, Rollwagen F, Denman DW, Hintz K, Hammer M, Crawford C, Henry K (2006). Can specific biological signals be digitised? FASEB Journal 20: 23-28.
Jones LL, Atkins P (2000). Chemistry: Molecules, Matter, and Change, Ch 5, p 382. WH Freeman and Co, New York.
Jorgensen WL and Madura JD (1985). Temperature and size dependence for Monte Carlo simulations of TIP4P water. Mol Phys 56 (6): 1381.
Kalko SG, Gelpi JL, Fita I, Orozco M (2001). Theoretical study of the mechanism of substrate recognition by catalase. J Am Chem Soc 123: 9665-9672.
Kamerlin SCL, Warshel A (2010). At the Dawn of the 21st Century: Is Dynamics the Missing Link for Understanding Enzyme Catalysis? Proteins 78(6): 1339-1375.
Kassirer JP (2007). On the Take: How Medicine’s Complicity with Big Business Can Endanger Your Health. Oxford University Press, USA.
Kauzmann W (1959). Some factors in the interpretation of protein denaturation. Adv Protein Chem 14: 1-63.
Kent M (2000). Advanced Biology, p 43. Oxford University Press, Oxford, UK.
Klotz MG, Loewen PC (2003). The molecular evolution of catalytic hydroperoxidases: Evidence for multiple lateral transfer of genes between prokaryota and from bacteria into eukaryota. Mol Biol Evol 20: 1098-1112.
Koppenol W.H (2001). The Haber-Weiss cycle – 70 years later. Redox Report 6(4):229–234.
Koshland DE (1958). Application of a theory of enzyme specificity to protein synthesis. Proc Natl Acad Sci USA 44(2): 98-104.
Kohler RE (1973). The Enzyme Theory and the Origin of Biochemistry. Isis 64(2): 181-196.
Kurian P, Dunston G, Lindesay J (2014). Does quantum entanglement in DNA synchronise the catalytic centres of type II restriction endonucleases? arXiv:1403.5342v1 [physics.bio-ph] 21 Mar 2014.
Lane N (2010). First breath: Earth’s billion-year struggle for oxygen. New Scientist, issue 2746, 5th of February.
McCord JM, Fridovich I (1988). Superoxide dismutatse: the first twenty years (1968-1988). Free Radic Biol Med 5(5-6): 363-9.
Milgrom LR (1997). The Colours of Life, and references therein, Oxford University Press, Oxford.
Milgrom L (2001). Thanks for the memory. The Guardian, 15th March.
Milgrom L (2014). “Living is easy with eyes closed….” on blinded RCTs and specific and non-specific effects of complex therapeutic interventions, and references therein. Eur J Integ Med 6: 552-559.
Moin ST, Hofer TS, Randolf BR, Rode BM (2012). An ab initio quantum mechanical field molecular dynamics simulation of hydrogen peroxide in water. Comput Theoret Chem 980: 15-22.
Mollenhauer HH, Morre DJ (1978). Structural compartmentalisation of the cytosol: zones of exclusion, zones of adhesion, cytoskeletal and intercisternal elements. In: Subcellular Biochemistry vol 5, pp 327-362. Ed Roodyn DB. Plenum Press, NY.
Morrell NC (2008). Reactive oxygen species: finding the right balance. Circulation Res 103: 571-2.
Murthy MR, Reid TJ, Sicignano A, Tanaka N, Rossmann MG (1981). Structure of beef liver catalase. J Mol Biol 152: 465-499.
Oberley TB, Oberley LW (1997). Antioxidant enzyme levels in cancer. Histol Histolpathol 12: 525-535.
Olsen MMH, Siegbahn PEM, Warshel AJ (2004). Simulations of the Large Kinetic Isotope Effect and the Temperature Dependence of the Hydrogen Atom Transfer in Lipoxygenase. J Am Chem Soc 126(9): 2820-2828.
Partay LB, Jedlovszky P, Brovchenko I, Oleinikova A (2007). Formation of mesoscopic water networks in aqueous systems. Phys Chem Chem Phys 9: 1341-1346.
Pollack GH (2013). The Fourth Phase of Water: Beyond Solid, Liquid, and Vapour. Ebner & Sons Publishers, Seattle, Washington, USA.
Pollack GH (2013). Comment on “A theory of macromolecular chemotaxis” and “Phenomena associated with gel-water interfaces: Analyses and alternatives to a long-range ordered water hypothesis. J Phys Chem 117: 7843-7846.
Reid TJ, Murthy MR, Sicignano A, Tanaka N, Musick WD, Rossmann MG (1981). Structure and haem environment of beef liver catalase at 2.5 Å resolution. Proc Natl Acad Sci USA 78: 4767-4771.
Rhodes CJ (2011). Can free radicals be good for you? Sci Prog 94(4): 451-462.
Rousseau DL, Porto SPS (1970). Polywater: polymer or artefact? Science 167: 1715-1719.
Schurr JM, Fujimoto BS, Huynh L, Chiu DT (2013). A theory of macromolecular chemotaxis. J Phys Chem 117: 7626-7652.
Schurr JM (2013). Phenomena associated with gel-water interfaces: Analyses and alternatives to a long-range ordered water hypothesis. J Phys Chem 117: 7655-7674.
Shakespeare S (1623). The Tragedy of MacBeth, Act 5 Scene 5. First Folio.
Sies H (1993). Strategies of antioxidant defence. Eur J Biochem 215(2): 213-9.
Stauffer D (1985). Introduction to Percolation Theory. Taylor and Francis, London and Philadelphia.
Stryer L, Berg JM, Tymoczko JL (2002). Biochemistry (5th ed). WH Freeman, San Francisco.
Subramanian D, Anisimov MA (2014). Phase behaviour and mesoscale solubilisation in aqueous solutions of hydrotropes. Fluid Phase Equil 362: 170-176.
Sulbaran B, Toriz G, Allen GG, Pollack GH, Delgado E (2014). The dynamic development of exclusion zones on cellulosic surfaces. Cellulose 21: 1143-1148.
Sumner JB, Dounce AI (1937). Crystalline catalase. Science 85: 366-367.
Tanford C (1968). Protein denaturation. Adv Protein Chem 23: 121-282.
Thomas Y, Schiff M, Belkadi L, Jurgens P, Kahhak L, Benveniste J (2000). Activation of human eutrophils by electronically transmitted phorbol-myristate acetate. Med Hypoth 54(1): 33-39.
Thornberry N, Lazebnik Y (1998). Caspases: enemies within. Science 281(5381): 1312-1316.
Vainshtein BK, Melik-Adamyan WR, Barynin VV, Vagin AA, Grebenko AI (1981). Three-dimensional structure of the enzyme catalase. Nature 293: 411-412.
Watson J (1995). The quantum of water and protein and the structure of the cell. In: Quantum Worlds, chapter 5. WH Freeman and Co, New York.
Watterson JG (1991). The interactions of water and proteins in cellular function. Prog Mol Subcell Biol 12: 113-134.
Watterson JG (1996). Water clusters: pixels of life. In: Toward a Science of Consciousness, pp 397-405. Eds Hameroff SR, Kaszniak AW, Scott A. MIT Press, Cambridge, Massachusetts, USA.
Watterson JG (1997). The pressure pixel: unit if life. Biosystems 41: 141-152.
Yoon DS, Won K, Kim YH, Song BK, Kim SJ, Moon SJ, Kim BS (2007). Continuous removal of hydrogen peroxide with immobilised catalase for waste water reuse. Water Sci Technol 55(1-2): 27-33.
Yoshida H, Ise N, Hashimoto T (1995). Void structure and vapour-liquid condensation in dilute deionised colloidal dispersions. J Chem Phys 103: 10146.
Zamocky M, Fortmuller PG, Obinger C (2008). Evolution of catalases from bacteria to humans. Antioxid Redox Signal 10: 1527-1548.
Zheng J-M, Chin W-C, Khijniak E, Khijniak E Jr, Pollack GH (2006). Surfaces and interfacial water: Evidence that hydrophilic surfaces have long range impact. Adv Colloid Interface Sci 127: 19-27.
Web References
[1] Enzyme Kinetics. www.uscibooks.com/changten.pdf Accessed 04/18/2015.
[2] McDowall J. Catalase. www.ebi.ac.uk/interpro/potm/2004_9/Page1.htm Accessed 02/07/2015.
[3] Goodsell D. Molecule of the Month, Sept 2004. pdb101.rcsb.org/motm/57 Accessed 04/02/2015.
[4] Free radicals good for you? Banned herbicide makes worms live longer. www.sciencedaily.com/releases/2010/12/101220084442.htm Accessed 04/02/2015.
[5] Chaplin MF. Water structure and science. www1.lsbu.ac.uk/water/memory_of_water.html Accessed 03/13/2015.
[6] Watterson JG. Enzyme Function: Random Events or Coherent Action? www.lsbu.ac.uk/water/watterson.pdf Accessed 3/20/2015.
[7] Chaplin MF. ‘Polywater’, declustered water, and other waters. www1.lsbu.ac.uk/water/polywater.html Accessed 3/24/2015.
[8] Baker C. Decomposing hydrogen peroxide www.rsc.org/Education/EiC/issues/2007May/ExhibitionChemistry.asp Accessed 4/1/2015.
[9] Evidence-based acupuncture: www.evidencebasedacupuncture.org Accessed 3/17/2015.
[10] The British Homeopathic Association www.britishhomeopathic.org/evidence/the-evidence-for-homeopathy/ Accessed 3/17/2015.
[11] Khorsandi-Taskoh A. Interdisciplinary Higher Education: Criticism, challenges, and obstacles.ir.lib.uwo.ca/cgi/viewcontent.cgi?article=1014&context=researchday Accessed 3/17/2015.
