On Fractal Geometry for Water Implosion Engineering

On Fractal Geometry for Water Implosion Engineering

---

Jurendic T¹, Pavuna D^2*

¹Department of Industrial and Physical Pharmacy, Purdue University, West Lafayette, IN 47907, USA

¹Bioquanta Inc., Dravska 17, HR-48000 Koprivnica, Croatia 

²Physics Section, Ecole Polytechnique Federale de Lausanne (EPFL) Station 3, FSB, CH-1015 Lausanne, Switzerland

^*Correspondence E-mail: [email protected]

Key Words: fluid mechanics, fractal geometry, implosion engineering, vortex, water clusters

Received March 22nd, 2012; Accepted June 11th, 2012; Published December 9th, 2012;

Available online December 15th, 2012

doi: 10.14294/WATER.2012.7

 

Summary

Historically water engineering was predominantly treated within a conventional mathematical framework, like Bernoulli approach or more advanced Navier-Stokes equations; lately by various numerical modeling schemes. Here we outline how the natural, yet complex water (and related fluids) flow and implosion engineering can successfully be treated by contemporary fractal mathematics. Such an approach could gradually improve our fluid engineering and the planetary use of natural water in bio-medical, transport and energy context.

 

Article Outline

• Introduction
• Discussion
• Conclusions
• Acknowledgements
• References
• Discussion with Reviewers

 

Introduction

Despite remarkable technological successes, everyone who teaches introductory university physics (science) courses is aware how patchy our understanding of contemporary physics and science is in general. Moreover, while our data production is growing exponentially, we cannot claim an exponential progress in our understanding of nature. The progress seems rather slow in classical fluid and practical water engineering, due to the simple fact that we mostly teach engineers to use rather conventional mathematical approximations (Constantin and Foias, 1988), even though there exists much more potent, and well established, mathematical approaches. In this brief paper we outline a more appropriate approach to water (and related fluids) by using fractal mathematics (Mandelbrot, 1983) in the context of fluid engineering. Such an approach could gradually enable numerous, useful engineering applications, specially in the implosion pump development and related environment friendly technologies.

 

Discussion

It was recognized already in the 1930s that spiral motion is a basic form of the motion of water in nature, and that was later the basis for some nature-friendly technologies (Bartholomew 2010). The combined spiral and chaotic motions produce the so-called vortex (see Fig.1).

An actual vortex can be observed as the bathwater goes down the plughole. The Coriolis Effect determines the rotation direction of spiraling water’s vortex motion. The reason for this type of motion is that water always tries to follow the path of least resistance rather than the shortest straight path. The vortex forms as a result of acting gravitational and Coriolis fields and enables water to reduce flow resistance by curving inwards. In such a way any resistance caused by usual straight motion disappears. As water implodes in the vortex, the matter at the exterior of the vortex moves more slowly than in the center and that causes the emergence of a strong centripetal force. The suction process that causes matter to move inwards is called implosion. The implosion vortex motion causes the increase in density, the pressure and the flow speed, a temperature drop and a reduction of frictional resistance.

 

---

Figure 1: Schematic illustration of the water vortex.

---

 

In the implosion process the centripetal form of motion dominates. This type of matter motion results in cooling, structuring and condensing. Therefore in the implosion water vortex system (Fig. 1) water is cooled, structured and condensed. The term “structured” is understood as the property of the higher order system. Higher structured liquid water is nothing else than the ensemble of water clusters which consist of more than one water molecule. Such clusters can be observed whenever irregular water molecules build higher order systems.

Different polygonal water structures (clusters) were reported by Jhon (2004). He developed the hexagonal water structure theory that explains the existence of three different water cluster shapes. There are hexagonal hook-shape, hexagonal chain-shape and pentagonal hook-shape. The water molecules do not exist separately in the water system, but rather as a cluster of molecules. It was indeed proven by Chaplin (2009), that in liquid water, the water molecule does not propagate ‘isolated’, but in clusters that are continuously forming and dissociating. Water clusters held together by many hydrogen bonds have lower molecular density and are favored at lower temperatures and pressures (Chaplin, 2009). The structured model for water proposed by Chaplin (2012) contains a mixture of hexagonal and pentagonal substructures and contains cavities capable of enclosing small solutes. This model was developed by arranging alternating sheets of boat-form and chair-form water hexamers from the lattices of hexagonal and cubic ice respectively. This structure was folded to form an icosahedral three-dimensional network with capacious pores capable of partial collapse due to competition between bonded and non-bonded interactions. Such clusters appear to be relatively stable in liquid water, forming curved surfaces when bound together by means of the three potential hydrogen bonds on each of their faces (Chaplin, 2012). Thirteen icosahedra can theoretically build an icosahedra super cluster.

Although it may appear that all the above mentioned clusters are regularly shaped, it is not completely true. The aforementioned examples clearly show that at a molecular level the liquid water is a mixture of diff-erent water clusters and water molecules. Independently of that approach, if the liquid water is taken to be an ensemble of clusters, or of water molecules, it is obvious that at a molecular level the liquid water is an irregularly shaped natural object that cannot be appropriately described by using usual (Euclidean) geometry.

Some Insights From Fractal Geometry

A simple bathwater example illustrates that the prevailing natural movements are non-linear. Inward spiral (centripetal) water motion is non-linear motion and one possible way to describe such a system from the mathematical point of view is within fractal geometry.  

The concept of fractal geometry, introduced by Benoit B. Mandelbrot, provides a solid platform for the analysis of the aforementioned natural phenomena. We are dealing with mathematics of non-smooth objects that can be characterized as a general framework for the study of irregular sets. Irregular sets provide a much better representation of many natural phenomena than do the figures of “classical” Euclidean geometry (Falconer, 2003). The term fractal can be described as an irregular object that does not fit into a classical geometrical setting, as a set which shows irregularities on all scales, or as proposed by Mandelbrot as a set with Hausdorff dimension strictly greater than its topological dimension. More about Hausdorff dimension can be found in the literature (Mandelbrot, 1983; Falconer, 2003). Following these definitions, many fractals can be easily observed in nature in the form of clouds, islands, rivers, trees, waves, fluid motions, etc. 

For this work, of particular interest are a water molecule and the dynamical implosion water vortex system. The central role in fractal geometry is played by dimension, meaning number of dimensions or dimensionality (Mandelbrot, 1983). In this sense it is important to describe the term fractal dimension. In literature many different definitions of fractal dimensions have been proposed, yet following Mandelbrot’s definition of the fractal, fractal dimension can be observed as Hausdorff dimension. It is well known that in Euclidean dimensions (D) objects can be observed as zero-dimensional (D=0), one-dimensional (D=1), two-dimensional (D=2) or three-dimensional (D=3). The example of a zero-dimensional object is a point, one-dimensional is a curve, two-dimensional is a surface and three-dimensional is a volume. In fractal dimension (DF) observed objects can be larger or smaller than one-, two- or three-dimensional. One example of fractal dimension represents one of the best known fractals, called the Cantor set, whose dimension is DF=0.631 (Mandelbrot, 1983). It means that in fractal dimension, the fractal object shows inter dimensional properties. Fractals can also be one-, two- or three-dimensional, as in classical geometry, but more frequent is the case where the fractal is, for example, more two-dimensional than three-dimensional, or vice versa. 

Today’s fluid statics and dynamics often approximate natural shapes by using classical (Euclidean) geometry approach. From the aforementioned reasons, it is clear that the liquid water system is irregularly shaped. For better understanding of both fluid statics and dynamics and especially water system behavior, a new approach dealing with irregular natural water molecule shapes by using fractal geometry is of high importance. Using such an approach it is possible to develop new mathematical relations that take into account all shape depending properties and much more.

Looking at implosion water vortex system from the fractal geometry viewpoint, there are two possible approaches, top-down and bottom-up.

Top-down Approach

The top-down approach deals with the whole vortex system, where a vortex alone can be considered as a fractal object that consists of water clusters which are also fractal objects; those then consist of water molecules as fractal objects, and so forth. In this sense the vortex system could be studied as a continuous dynamical system with a fractal attractor. An attractor is a set to which all nearby orbits converge (Falconer, 2003). The Lorenz system of equations is one example of such a system (Lorenz, 1963). Lorenz studied the thermal convection of a horizontal layer of a fluid heated from below and developed deterministic ordinary nonlinear differential equations to represent forced dissipative hydrodynamic flow. He emphasized that certain mechanically or thermally forced non-conservative hydro dynamical systems may exhibit either periodic or irregular behavior when there is no obviously related periodicity or irregularity in the forcing process. Both periodic and non-periodic flow is observed when the forcing process is held constant.

Analogously to Lorenz’s oscillator (three-dimensional non-linear dynamical system that exhibits turbulent flow and evolves over time in a complex, non-repeating pattern) (Lorenz, 1963), the water vortex system can be characterized as a non-linear hydro dynamical system that exhibits a turbulent flow.

By using Navier-Stokes equations, continuity equations and heat conduction equations, Lorenz has developed three differential equations (Falconer, 2003). Solutions of these equations can be identified by trajectories in the phase space (Lorenz, 1963). The trajectories are concentrated onto a Lorenz attractor that consists of two discs each made up of spiraling trajectories. Certain trajectories leave each of the discs almost perpendicular and flow into other discs, exhibiting a chaotic behavior (Falconer, 2003). This Lorenz attractor seems to be a fractal of Hausdorff dimension 2.06; similarly to Lorenz’s study where thermal convection was studied, the dynamical water vortex system must be studied individually.The water vortex system can be considered as an open or closed system. An open water vortex system corresponds to the water flow out of vortex following spiral path, while the closed system represents the situation in which the water does not flow out.

As a closed hydro dynamical system of finite mass the water vortex system can be mathematically treated as a finite collection of molecules: In such a case the governing laws can be expressed as a finite set of ordinary differential equations; these are generally highly intractable. In order to propose soluble equations, the vortex system could be approximated by a continuous mass distribution. In this sense the governing laws can be expressed as a set of partial differential equations, with dependent variables: pressure, temperature, velocity and density. In such a system as in any real hydro dynamical system, viscous dissipation is expected to occur.

So, due to various natural phenomena that exhibit turbulent and non-periodic flow with a non-smooth surface, the water vortex appears to be a rather interesting and challenging object of study for the applications of fractal mathematics.

Bottom-up Approach

The other possibility to deal with the vortex within the fractal geometry approach is to consider a water molecule as a fractal object. A water molecule consists of one oxygen and two hydrogen atoms. The basic geometric structure of water molecule shows that hydrogen-oxygen-hydrogen angle is from 104.45° in liquid water to 109° in the ice. Such irregular geometric water structure can be considered as a non-linear object. As a water molecule is a structure with an irregular shape, using fractal geometry to determine its characteristics seems rather natural.  So, let us consider a water molecule as a fractal object F, with a fractal dimension, D_F. Because of its nonspecific shape, according to the Hausdorff approach, the fractal F may be covered with balls b, of  diameter d_b, whose measurement unit is γ = d_b^α, where α is Hausdorff exponent. Therefore, α-covering measure M can be defined as follows:

(1)

where ε is a measurement unit for identical specific shaped objects (boxes). In this sense ε can be the length of the box side, if the object is a box. In our case object F is irregular and as proposed by Hausdorff, ε is replaced by d_b. Therefore, fractal dimension D_F is defined:

(2)

(3)

Without introducing further mathematical considerations it is important to underline that the Hausdorff measures generalize well-known ideas of volume, surface and length. As mentioned by Falconer (2003) it is possible to determine the volume of α-dimensional ball of diameter 1. If the water molecule fractal F can be represented as a sum of balls of diameter d_b, and if it is possible to determine volume of each ball, it should be possible to determine the fractal dimension of the water molecule. 

As we already noted, the water clusters exist in the liquid water and consist of water molecules (Fig. 2). Cluster building, in this sense, can be represented as a process of water molecules aggregation. As a natural object, a water cluster grows in an apparent fractal form, because it is composed of irregular shaped fractals, respectively water molecules. Aggregation, as an assumed process for cluster building, can be defined as a physical process in which clusters are built up from water molecules. Dealing with iron particles, Forrest and Witten (1979) have observed that aggregates have fractal structures. They interpreted the aggregation in terms of the scaling laws.

Scaling properties are of high importance in order to understand the fractals. In fractal theory, the scaling properties of α-dimensional Hausdorff measure Mα is λα (Falconer, 2003).  Similar to the Forest and Witten (1979) approach, the fractal dimension of a water cluster could be obtained using the density-density correlation function g(R) (Vicsek, 1999):

(4)

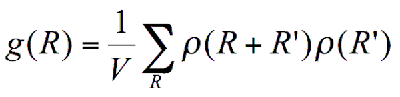
Where ρ(R) is a local density at the point R. ρ(R) is equal to 1 if the point is a part of a  fractal object. If that is not the case ρ(R) is equal to 0. As mentioned above, the volume of the fractal object V is equal to the number of the covering balls N. The number of covering balls N with radius s in the D dimensional volume can be found through:

(5)

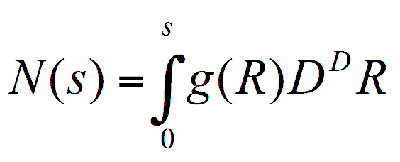
Given the density-density function, from this follows the power law behavior g(R) ∝ R^-G. The relation between the density-density correlation function G, Euclidean dimension D and fractal dimension D_F is D_F=D-G. G can be defined using a linear fit of ln(g(R)) as a function of ln(R). 

When the fractal dimension of the water cluster is known, it is possible to determine the fractal dimension of the whole vortex system. In literature exists other known approaches to define D_F , yet in this short paper our intention is only to point out that the water system can be meaningfully considered as a fractal object on different scales.

Implications For Fluid Dynamics

The goal of the two previous approaches (top-down and bottom-up) was to suggest that the water system is a fractal object and should be treated as such. The main applications of such approaches are in fluid dynamics, where part of the water system is always represented as a regularly shaped object.  This immediately seems inadequate when one is aware of the irregularly shaped water molecules. Although at the microscopic level they are connected in “regular” pentagonal, hexagonal or other structures, the actual water molecules are not regular. Because of the irregular water molecule structure, one hydrogen atom remains always outside the structure. Therefore, all actual clusters are irregular.

The description of icosahedral water model can be even more complicated, i.e., one can use the sphere, cylinder, cube, etc. By using the fractal geometry approach, the water cluster can be represented in the form that actually is observed in the nature, avoiding oversimplifying approximations of classical geometry.

Independently, whether the considered water molecule is a pentagon, hexagon, tetrahedron or icosahedron, it is obvious that all these objects are irregularly shaped. Therefore, a serious task of fractal geometry is to define the icosahedral or any other water molecular model as a fractal object. If the water cluster can be described by fractal geometry (reasons are given above), there is a logical extension that the implosion water process that produces water clusters (higher order structure) can also be described within the fractal geometry framework.

All aforementioned structures of water molecule, polygonal structures, icosahedra or vortex system cannot be completely described and understood by using the classical approach, yet can be treated within the fractal mathematics. Defining such clusters (with all irregularities) in more appropriate ways opens up a completely new approach in study of the fluid dynamics. A natural fractal is used as a study object within the fluid dynamics.

The core object in fluid dynamics is no longer a sphere, cylinder or cube, as a part of the water system, but rather the water fractal, which is natural, self-similar and nicely fits the real situation. Fig. 2a shows water fractals (water molecules and water pentagonal cluster) inside the pipe. As can be seen such structures are not possible to represent using natural geometry. The same situation can be observed by representing of water icosahedral cluster (Fig. 2b). 

 

---

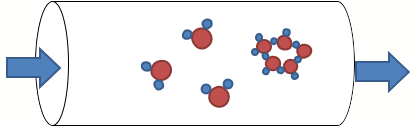
Figure 2a: Water molecules and a water pentagon as fractals. 

Figure 2b: Water icosahedral cluster as a fractal. 

---

 

Developing appropriate mathematical models to describe vortex behavior formed by implosion, by using fractal geometry, will be a good basis for understanding the mass, heat and momentum transfer in the whole system.

Observing vortex systems as a closed hydrodynamical system of a finite mass and from the mathematica equations. Such differential equations. Such differential equations should contain characteristics features of a vortex in the form of dependent variables as pressure, temperature, velocity and density. In treating a finite dynamical system such as a vortex, phase space concept, solutions of appropriate differential equations are very useful. To better understand the implosion process, the detailed study of pressure, temperature and velocity gradient is of great importance, as well. Henceforth it is possible to determine all the crucial parameters and transport properties in the implosion process.

Better in-depth understanding of the implosion phenomenon from the mathematical and engineering points of view represents a good basis for the development of new sustainable and modern equipment, processes and technologies. Fig. 3 represents the scheme of the pneumatic water turbine, one example of many possible future nature-friendly machines.

 

---

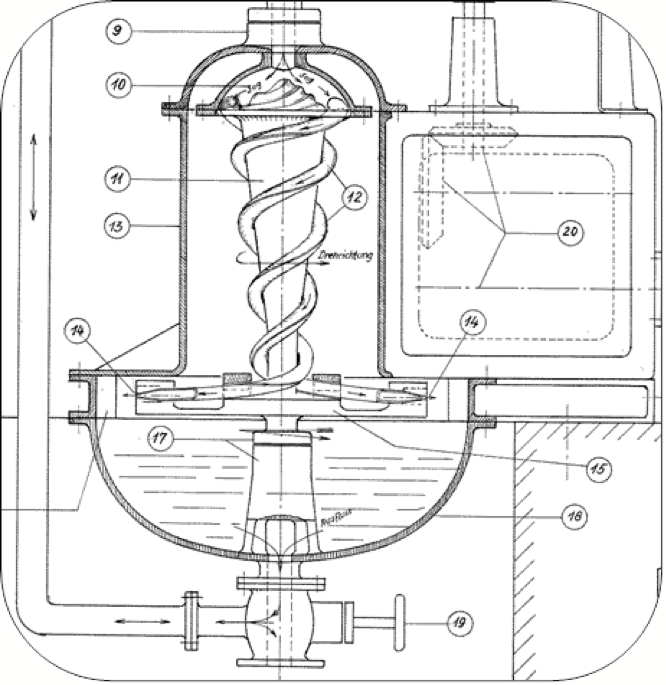
Figure 2b: Schematic diagram of the Pneumatic Water Turbine.

---

 

Given its rather high complexity, the study of implosion phenomena requires a coordinated and truly interdisciplinary approach.

 

Conclusions

In this brief paper we have outlined how a fractal mathematics approach could be used in studies of water flow and implosion processes in contemporary engineering. Given new discoveries and insights into the behavior of water (Pollack, 2010), we argue that such an approach and future extensions in related engineering/mathematical problems may gradually influence the worldwide water management and improve our planetary water (and related fluids) engineering within a better, nature friendly civilization.

 

Acknowledgements

We gratefully acknowledge discussions with many colleagues worldwide, most notably with Gerald Pollack, Urs von Gunten, Gunther Pauli, Klaus Rauber and Ina Matijevic.

 

References