Domains Formation Mediated by Electromagnetic Fields in Very Dilute Aqueous Solutions: 1. Quantum Electrodynamic Aspects

Domains Formation Mediated by Electromagnetic Fields in Very Dilute Aqueous Solutions: 1. Quantum Electrodynamic Aspects

Yinnon TA1*,  Liu ZQ2

1 K . Kalia, D.N. Kikar Jordan 90666, Israel

2 Department of Physics Qufu Normal University, Qufu, 273165, China

*Correspondence E-mail: lwcdsrc@kalia.org.il

Key Words: Water aggregates; molecular associates; coherence domains; ferroelectric orderings; polar liquid solutions; aqueous solutions; quantum electrodynamics.

Received Jan 15th 2015; Revised June 4th; Accepted June 30th; Published Aug 10th; Available online Oct 25th, 2015

doi: 10.14294/WATER.2015.4

 

Abstract

10-7 – 10-4 m sized molecular groupings in solutions are the foci of our research. The concentration of the solutions varies from 2 M to 10-20 M. The solutions are prepared by serial dilutions of a stock solution with polar solvents (e.g., water) and vigorous shaking after each dilution step. Light scattering, dielectric permittivity, electric conductivity, pH and others measurements, reported in previous publications, evidenced: (i) electromagnetic fields mediate formation of the groupings; (ii) the impact of the groupings on some of the solutions’ physicochemical properties (e.g., electric conductivity) is correlated with their bioactivity. The aim of our current research is analyzing experimental data pertaining to the groupings’ characteristics and confirming that these agree with those predicted by quantum electrodynamics (QED). Towards this aim, in the current paper we provide a concise overview of recently derived predictions of QED relevant to molecular groupings in solutions. We also cite publications presenting experimental data verifying some of these predictions. In the two following papers in this journal’s issue, we employ QED for analyzing recent published experimental data pertaining to groupings in solutions of, respectively, strong electrolytes and other solutes (weak electrolytes, non-electrolytes).

 

Article Outline

 

Introduction

Down to ultra low concentrations (C) – about 10-20 M – serial diluted vigorously shaken polar liquids (SDVSPL) may affect bio-systems (Palmina et al., 1994; Konovalov et al., 2008, 2014a; Konovalov and Ryzhkina 2014b) a. The biological active solutes include inorganic-, organic- or bio-molecules, strong or weak electrolytes. For example, pesticides, poisons, synthetic or natural remedies affecting enzymes, membranes and organisms. In ultra low concentrated (ULC) SDVSPL at ambient conditions, part of the solvent molecules form groupings, as initially revealed with calorimetric, electric conductivity and pH data; serial diluted solutions, which at each dilution step are not vigorously shaken, do not contain groupings for C below a solute type dependent critical concentration (Ccrit); typically ~10-8 M < Ccrit <~10-6 M (Elia and Niccoli, 1999, 2000, 2004a, 2004b). The groupings comprising 10-7 – 10-5 m sized molecular associates, their electrokinetic potential and their impact on the liquid’s dielectric permittivity were first uncovered with dynamic light scattering, electrophoresis and dielcometric titrations, respectively (Konovalov et al., 2008; Ryzhkina et al., 2009). Stabilization of the groupings occurs during the period of about 1-18 hours after the SDVSPL’s preparation. For 10-13 M < C <10-3 M aqueous SDVSPL of strong electrolytes, transmission electron microscopy, atomic force microscopy and dielectric permittivity data revealed presence of 10-5 – 10-4 m sized molecular associates (Lo et al., 1996, 2009; Ho, 2014).

a SDVSPL preparation involves serial decimal or centesimal diluting a “stock” solution. Hitherto, mainly aqueous SDVSPL have been studied, but solutions with other solvents were also investigated. Aqueous SDVSPL are prepared with freshly doubly distilled water or water purified by Simplicity®Water Purification Systems – Millipore, with specific electrical conductivity below 2.5 μS/cm. Dust is removed. Stock solutions are analyzed for absence of impurities. C of stock solutions are in the 4 M – 10-3 M range. After each dilution step, SDVSPL are vigorous shaken, e.g., with lab dancer shaker, by vertical vortexing or other methods. Plastic or glass vessels are used. Temperature and pressure are kept constant, typically, respectively,  at 298 K and ~1 Atm. As controls, the solvent (e.g., doubly distilled water) is serial diluted and shaken after each dilution step, with all experimental parameters identical to those of SDVSPL preparation.

For solute type dependent C ranges, correlation was observed between the solutions’ bioactivity, electric conductivity, the groupings’ effective hydrodynamic diameter and electrokinetic potential; all these properties non-linearly depend on C and are reproducible (Konovalov et al., 2014c). Not for all kinds of solutes, their ULC SDVSPL contain groupings. For some solute types their ULC SDVSPL have the customary characteristics of infinite diluted solutions (Konovalov, 2013). Solute attributes required for inducing groupings and the origins of their physical, chemical, catalytic and bio-active properties are not yet clarified. Impurities released by containers affect SDVSPL but cannot account for their typical properties. For a concise discussion of impurities’ effects see Yinnon and Liu (2015a).

As to forces underlying the groupings formation, electrodynamic ones play a role — electromagnetic fields (EMF) affect aqueous SDVSPL containing groupings (Montagnier et al., 2009; Ryzhkina et al., 2011; Elia et al., 2012; Konovalov et al. 2014a,b). On storing samples under hypo electromagnetic conditions, i.e., in a Permalloy container with residual field of 10 nano Tesla, no groupings are observable for 10-20 M<C<Cthr; weak EMF influence the groupings for Cthr <C<~10-4 M. The threshold concentration Cthr is solute type dependent, typically 10-10 M<Cthrr<10-6 M.

Customary models of ULC solutions at ambient conditions cannot account for SDVSPL’s properties. These models predict that: EMF, serial dilutions or vigorous shaking do not affect SDVSPL characteristics; solvated solutes distribute homogenously, move independently and randomly; polar solvent molecules (except solvation shells’ solvent molecules) move randomly; for aqueous solutions, its water molecules (H2O) form flickering hydrogen-bond networks (Horne, 1971). These customary models explicitly include electrostatic forces and assume electrodynamic ones can be treated perturbatively. However, quantum electrodynamic (QED) models explicitly including electrodynamic forces show interactions between EMF and liquid molecules may lead to formation of various domains (Del Giudice, 1988, 2000; Arani et al., 1995; Preparata, 1995 chapters 2, 5, 10; Yinnon and Yinnon, 2012). For example, EMF interactions with electrolytic solutes, polar solute molecules or with solvent molecules with sufficiently large electric dipole moments, for solute type dependent C ranges, may lead to distinctive domain types. Within the context of formal QED theory of polar liquids, the conditions for formation of these domains and their properties were ab initio derived. SDVSPL observed phenomena signify QED has to be employed for their explanation. Indeed, the QED model for SDVSPL proposed by Yinnon and Yinnon (2011) has provided consistent explanations for various phenomena, e.g., self-organization of molecules in SDVSPL, these liquids’ electric conductivity, heat of mixing and their dependence on time and volume (Yinnon and Elia 2013). 

Our study’s foci are: (a) employing QED for explaining recently observed (and to the best of our knowledge yet unexplained) characteristics of the various groupings present in SDVSPL; (b) elucidating the relation between these characteristics and the liquid’s properties, e.g., its dielectric permittivity, spectra and bioactivity.  As to their importance, SDVSPL have implications for numerous technologies and bio-processes. 

Since QED of polar liquids hitherto mainly is employed for explaining special phenomena, many readers may be unfamiliar with it. Its aspects relevant to our analyses of SDVSPL were derived in a series of publications published since 1988. Some of these publications contain many mathematical expressions. Therefore we deem it appropriate to provide a short overview of the topic to the non-physicists, i.e., an overview which uses intuitive arguments only. Of course avoidance of the rigorous mathematical technicalities implies we have to pay the price of some imprecision. For those interested to study the issues more in depth, we point out their sources. 

Based on the QED properties presented in our overview, Yinnon and Yinnon (2011) and Yinnon and Elia (2013) proposed a model for very dilute solutions. We will employ their model for explaining recently measured SDVSPL properties. Including in this paper a concise summary of their model and employing it for analyzing measured SDVSPL properties would make it excessively lengthy. Therefore, below we suffice with providing an overview of QED properties of polar liquids. In the two publications following this one (Yinnon and Liu, 2015a, 2015b) respectively, for SDVSPL of strong electrolytes and of other solutes (weak electrolytes, non-electrolytes), we will present their models and employ these for explaining recently observed phenomena.  

As to the outline of this paper, we first present an overview of polar liquids’ characteristics predicted by QED. The overview starts with some historical milestones pertaining to modeling effects of EMF on intermolecular interactions and thermodynamics of molecular ensembles. Next it focuses on structural aspects of the ensembles resulting from electrodynamic interactions, i.e.: phase transitions leading to formation of coherence domains; the physics underlying these domains; the domains’ effects on thermodynamics of the ensembles; formation of supra-domains; types of domains present in polar liquids or their solutions; properties of the various domains hitherto identified. After that, in the Discussion section, we shortly discuss the status of experimental data confirming characteristics of polar liquids predicted by QED. In the Conclusion section we point out some challenges ahead. A list with abbreviations we add at the end of this paper. We stress that in the following we do not derive any new features of QED.

 

QED Predictions for Polar Liquids’ Characteristics

Modeling Effects of EMF on Intermolecular Interactions

Assessing effects of electrodynamic forces on thermodynamic and structural properties of molecular ensembles for many decades posed numerous challenges. London (1930) showed that quantum fluctuations of the EMF affect intermolecular forces. Such fluctuations can be represented by virtual photons popping out of empty space (the quantum vacuum), as allowed by the uncertainty principle. These fluctuations are non-thermal — these persist when temperature vanishes. London applied second order perturbation techniques to the electrostatic interactions between molecular dipoles to account for quantum fluctuations. His approach was a non-relativistic one and pertinent only to interactions between molecules in vacuum over distances of the order of 10-10-10-9 m, e.g., rarefied gas. He derived that the fluctuations underlie the intermolecular dispersion force, which is a component of the van der Waals force. Casimir and Polder (1948) used fourth-order perturbation techniques to derive the interactions between molecules and the EMF over longer distances, i.e., distances of the order or larger than the molecules’ characteristic absorption wavelengths. At such distances, relativistic effects play a role. Their inclusion for example enabled explaining the Casimir effect, which exemplifies the considerably strength of the interactions mediated by virtual photons (Casimir 1948). After the advent of quantum field theory, which proved to be the most accurate physics theory, Dzyaloshinskii et al. (1961) employed it to study the interactions between molecules in a liquid and the EMF. Their approach is based on perturbation techniques and Feynman diagrams. It for example enabled them to derive the effects of dispersion forces on the thermodynamics of liquids.

Phase Transitions Induced by QED Interactions Leading to Coherence Domains

The aforementioned approaches treated interactions between molecules and the EMF as small perturbations. Albeit conditions for fluctuating EMF majorly affecting condensed matter, e.g., leading to phase transitions, were predicted (Dicke, 1953, Hepp and Lieb, 1973a,b). However, issues like the Hamiltonian’s form required for describing the interactions between the fluctuating EMF and molecules (Bialynicki-Birula and Rzazewski, 1979) for many years prevented their verification. Hence, a practical approach was adopted: condensed matter was modeled by explicitly including electrostatic interactions, while QED ones were described perturbatively or even ignored. The resulting theories explained numerous phenomena and led to the current customary models of polar liquids. Yet Preparata (1988, 1995) and Del Giudice et al. (1988, 1993) succeeded to resolve the aforementioned issues. They developed a non-perturbative (variational) quantum field theory model of liquids using the Feynman path integral. Their model enabled investigating phase transitions. They derived that QED interactions may lead to phase transitions whenever density and temperature are, respectively, above and below transition values. These values depend on variables like the coupling between matter and radiation. For water and other polar liquids, they showed that the transitions lead to auto-organization of a fraction of the liquid’s molecules in 10-7–10-4 m sized coherence domains (CD). This fraction depends on temperature. Within a CD, solvent or solute molecules coherently oscillate in-phase with a coherently condensed EMF. As to the molecules which do not join CD, these move randomly in the interstices between the CD. Independent research groups confirmed aforementioned (Sivasubramanian et al., 2001, 2002, 2003, 2005; Emary and Brandes, 2003; Apostel, 2009) 

The Physics Underlying Coherence Domains

For elucidating the physics underlying CD, we summarize explanations by Del Giudice et al. (1998), Preparata (1995 chapters 2,3,10), Arani et al. (1995) and Bono et al. (2012). Consider an ensemble of N molecules, which initially all move randomly within a volume Ve. Whenever the energy of a quantum fluctuation of the EMF (a virtual photon) equals that of a specific molecular excitation, all molecules within the volume spanned by the photon are candidates for excitation. This volume we denote Vphoton; it equals λ3, with λ denoting the photon’s wavelength. Vphoton contains about 106 – 1018 molecules, because electronic, vibrational or rotational excitations of molecules require 10-7 < λ < 10-4 m, while molecular sizes typically are about 10-9 – 10-10 m. The photon excites one molecule with probability Pr. The decay time of the excited state determines the durance of the molecule’s excitation. On de-excitation, the photon emitted can fly away or excite a second molecule. The probability PN that it excites another molecule is PN=Pr λ3 (N / Ve). For PN<1, the photon eventually returns to the quantum vacuum. However, when PN=1 [a condition occurring when N / Ve is larger than a transition density (N / Ve)trans], the photon loses the chance of leaving Vphoton and bounces from one molecule to another. Additional virtual photons may share the same fate, leading to a sizable EMF condensing within Vphoton b.  The condensed EMF causes all molecules within Vphoton to oscillate coherently between their ground state |0> and an excited state |b>. Accordingly, Vphoton was denoted Coherence Domain (CD). Since Ve can be partitioned into many Vphoton, other virtual photons may lead to more CD formations. Virtual photons with different λ initially may excite molecules to different |b>. However the system’s dynamics ultimately cause the molecules in all CD to oscillate between |0> and the same |b>. The coupling between the molecules and the EMF determines |b>. 

bThe condensation results from renormalization of the photon’s oscillation time when it interacts with the molecules. Due to the decay time of the molecules’ excited state, the frequency of a photon bouncing between molecules in a CD is smaller than the frequency of the free photon. According to the Einstein equation,  the differences in these frequencies causes the photons’ mass (which is zero for the free photon) to become imaginary. That is, the photons are unable to propagate, these are trapped as excitations of the molecules.

Thermodynamics of Molecular Ensembles Containing Coherence Domains

Only in open systems do CD form (Preparata, 1995 chapters 2,3,10; Arani et al., 1995). The energy of molecules in CD is lower than that of the ensemble’s randomly moving molecules. Accordingly, the energy gained on inclusion of a molecule within a CD has to be released to the environment as the phase transition’s latent heat. For ensembles in contact with a heat bath, temperature (T) determines the fraction of molecules included in CD. This fraction is an inverse function of T. Only below a transition temperature CD form. The energy a molecule gains on its inclusion within a CD is an inverse function of its distance from the center of its CD. When this energy is only slightly less than kBT (with kB the Boltzmann constant), the disruptive dynamics of thermal collisions may push molecules out of the CD. Therefore in specific temperature ranges, CD are meta-stable with molecules constantly desorbing and adsorbing at its surface.

Supra-coherence Domains

CD may agglomerate into supra-domains (supra-CD) (Preparata, 1995, chapter 10). Supra-CD are not ensembles of molecules but agglomerates of domains, like domains in liquid crystals. The agglomeration of CD is energetically favorable, because close packing of CD enables the evanescent tails of their condensed EMF to overlap and interfere constructively. As a result, within a supra-CD the oscillations of all molecules are coherent.

Types of Coherence Domains Present in Polar Liquids or Their Solutions

EMF interactions with electrolytic solutes, polar solute molecules or with solvent molecules with sufficiently large electric dipole moments, for solute type dependent C ranges, may lead to various CD types (Del Giudice, 1988, 1998, 2000; Arani et al., 1995; Preparata, 1995 chapters 2, 5, 10; Yinnon and Yinnon, 2012). The CD types and those of their properties required for modeling SDVSPL we summarize in the next paragraphs, using nomenclature of our previous publications. Hitherto identified CD include: 

  • CDelec, which are composed of solvent molecules only. Some of these molecules reside in an electronically excited state (see Figure 1). Their diameter is ~10-7 m.
  • CDrot, which are composed of ferroelectric ordered polar solvent molecules (see Figure 2). Their diameter is of the order of ~10-4 – 10-5 m.
  • CDplasma, which are composed of few solvated solutes and numerous polar solvent molecules (see Figure 3a). Their diameter is ~10-6 m. The plasma oscillations of their solute molecules are coherent.
  • IPDplasma, which are composed of few solvated solutes and numerous polar solvent molecules (see Figure 3b). Their diameter is ~10-6 m. The plasma oscillations of the solute molecules within IPDplasma are in phase, i.e., an IPDplasma is a  special CD — an In-Phase Domain.

To give the reader an intuitive feeling for the relative sizes of the CDrot, CDplasma and CDelec, we note their ratios are similar, respectively, to those of the sun, earth and moon.

 

Figure 1: Schematic view of a CDelec and its internal structure. Light-blue and yellow colored balls symbolize its molecules residing, respectively, in their ground and an excited electronic states. The molecules’ electric dipole moments, symbolized by arrows, are randomly oriented.
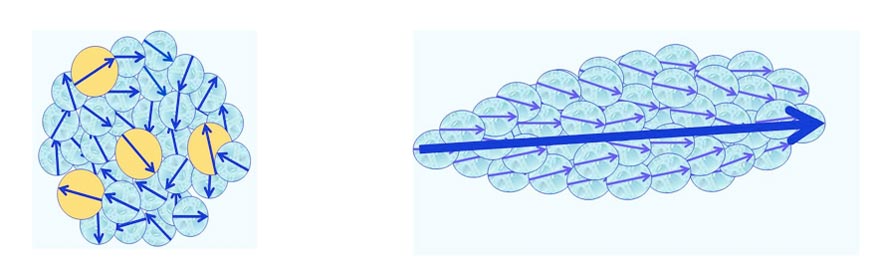
Figure 1: Schematic view of a CDelec and its internal structure. Light-blue and yellow colored balls symbolize its molecules residing, respectively, in their ground and an excited electronic states. The molecules’ electric dipole moments, symbolized by arrows, are randomly oriented.

Figure 2: Schematic view of a CDrot and its internal structure. Light-blue colored balls symbolize the molecules constituting the domain. Their blue arrows symbolize the molecules’ electric dipole moments. The large blue arrow symbolizes the electric dipole moment of the domain, resulting from the ferroelectric ordering of its molecules.

 

Properties of CDelec —

CDelec formation is mediated by ultra violet EMF (Arani et al., 1995; Preparata, 1995 ch. 10, Bono et al., 2012). Their formation is a central aspect of the condensation of a liquid from its vapor. Only for water the characteristics of CDelec have been derived.  We denote with the CDelec of water. The H2O constituting reside in a state which is a superposition of their ground |0> state (with a weight of about 87%) and the excited |b> state (with a weight of about 13%). One electron of an H2O residing in its |b> state is almost free (binding energy ≈ 0.4 eV). Hence, a is a pool of ~106 quasi-free electrons located at their boundary with ~7, 21, 35, 49,… kHz excited states, and correspondingly an ensemble of quasi free protons (the partners of the quasi-free electrons (Del Giudice et al., 1998, 2007). H2O are tetrahedrally ordered in . agglomeration in supra- underlie the hydrogen-bond network of bulk water.

Energy gained by a H2O’s inclusion in is ~0.17 eV at T=273 K and pressure of 1 Atm. only exist for temperatures below the transition temperature of 500 K. The fraction of H2O included in for T<180 K equals 1. For 180 K < T < 500 K, this fraction is less than 1. The H2O, which are not included in , move randomly in between or evaporate. Chemical potentials determine the fraction of H2O included within , percentages of H2O randomly moving in between and percentages of evaporated H2O. Bulk water and ice-Ih contain . At T=298 K, the fraction of H2O included in is about 20 percent. In bulk water, at ambient conditions, some H2O continually adsorb on while simultaneously others desorb from the domains, causing a ~10-14 s timescale flickering landscape. Thus observation requires fast resolution probes. Interfaces, CDrot, CDplasma and IPDplasma may stabilize and supra-, i.e., reduce their flickering, easing their observation. cannot contain solutes. Solvated solutes locate outside .

 

Figure 3 a-b: Schematic pictures of, respectively, CDplasma, and IPDplasma and their internal structures. Blue balls symbolizes solute molecules, with their yellow cosine curves symbolizing their plasma oscillations. For IPDplasma these oscillations are in-phase, for CDplasma these are just coherent. Light-blue colored balls symbolize polar solvent molecules. Their blue arrows symbolize their electric dipole moments. In IPDplasma these dipoles are spherically symmetric oriented around their nearest neighbor solute molecule. In CDplasma only the dipoles of H2O constituting the hydration shell are spherically symmetric oriented; all non-hydration shell solvent molecules are oriented randomly.

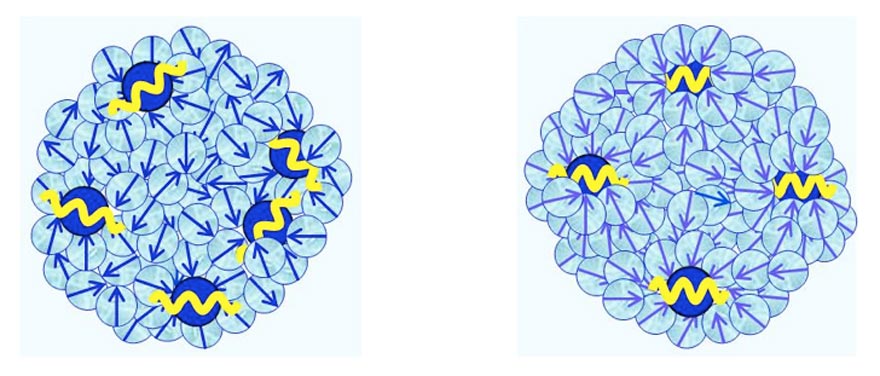
Figure 3 a-b: Schematic pictures of, respectively, CDplasma, and IPDplasma and their internal structures.Blue balls symbolizes solute molecules, with their yellow cosine curves symbolizing their plasma oscillations.For IPDplasma these oscillations are in-phase, for CDplasma these are just coherent. Light-blue coloredballs symbolize polar solvent molecules. Their blue arrows symbolize their electric dipole moments.In IPDplasma these dipoles are spherically symmetric oriented around their nearest neighbor solute molecule.In CDplasma only the dipoles of H2O constituting the hydration shell are spherically symmetricoriented; all non-hydration shell solvent molecules are oriented randomly.

 

Properties of CDrot —

CDrot formation results from their solvent molecules’ dipole moment interacting with Far Infra Red EMF (Del Giudice et al., 1988; Del Giudice and Vitiello, 2006). CDrot have an electric dipole moment due to the ferroelectric ordering of their solvent molecules (see Figure 2). In bulk water,  as well as in the bulk of many other polar liquids, at ambient conditions CDrot do not auto-organize. However, immersing objects with sizable asymmetric charge distributions (e.g., macromolecules, hydrophilic membranes) may induce their formation, resulting in a permanent time dependent polarization. Solutes are pulled into CDrot. Few solute particles can locate in CDrot and do not wreck their host. Many solute molecules destroy CDrot. Solute type determines critical C below which CDrot persist (). CDrot’s molecules coherently oscillate between two rotational states, resonating in-phase with the coherently condensed photons mediating their interactions.

QED CDrot are analogues of classical ferroelectric domains, which form due to an instability in the expression relating polarization density, polarization susceptibility and an external electric field (Sivasubramanian et al., 2005). QED, classical electrodynamic models, computer simulations and experimental data show that for bulk polar liquids at pressure of 1 Atm, CDrot may exist for temperatures below a transition temperature (Yinnon et al., 2015c — submitted to Water journal). For H2O the value of this transition temperature is 1160 K. Whenever the energy a solvent molecule gains by inclusion in CDrot is higher than kBT, the solvent molecules auto-organize into CDrot. Whenever this energy is lower than kBT, CDrott do not form spontaneously. However, by disturbing the liquid, for example by immersing a hydrophylic membrane into it, CDrot may form. On removal of the membrane, these CDrot are meta-stable and may persist for many months.

CDrot may agglomerate into supra-domains. Supra-CDrot may stabilize supra-. The latter are encapsulated in the former. Such assemblies we denote │supra-CDrot<supra->│. The state of H2O belonging to both CDrot and is a superposition of the state typifying the H2O constituting CDrot and the state typifying the H2O constituting . In Figure 4 we present a schematic picture of bulk water containing macromolecules with sizable asymmetric charge distributions which stabilize │supra-CDrot <supra->│.

 

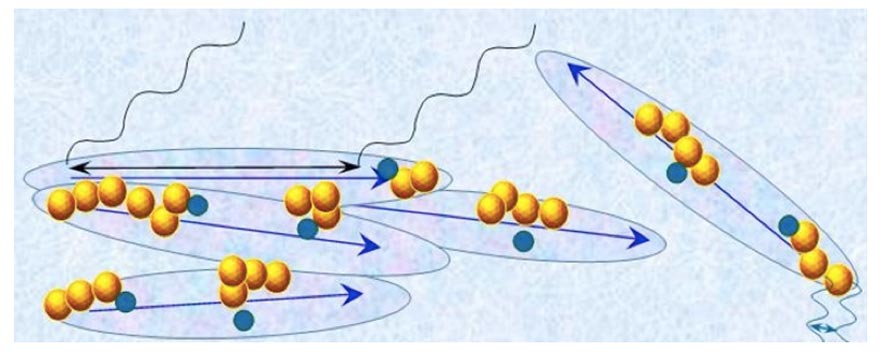
Figure 4: Schematic picture of bulk water containing macromolecules (represented by dark-blue balls)with a sizable asymmetric charge distributions at C< , i.e., at concentrations below the critical concentration for CDrot formation. The water contains large elongated domains. These represent the10-5-10-4 m CDrot stabilized by the macromolecules. The blue arrows represent the electric dipole moments of CDrot, resulting from their ferroelectric ordered H2O. Yellow-brown colored balls and their agglomerates represent, respectively, ~10-7 m sized and supra- . These are locatedin CDrot. are stabilized by CDrot. The agglomerates of elongated domains and the yellow-brownballs represent the │supra-CDrot<supra-CDelecH2 0 >│. The various domains and macromolecules sizes are not presented according to their realistic scale ratios. The black cosine curves represent Far Infra Red(FIR) EMF facilitating interactions (symbolized by black double arrow) among H2O over 10-5-10-4 m distances.These interactions underlie CDrot formation. The blue cosine curves represent UV EMF facilitatinginteractions (symbolized by blue double arrow) among H2O over 10-7 m distances. These interactions underlie formation.

 

Properties of CDplasma and IPDplasma —

CDplasma form when <C< and IPDplasma when C<, due to interactions between solutes and tetra Herz to mega Herz EMF (Del Giudice et al., 2000; Yinnon and Yinnon, 2012). At , CDplasma transform into IPDplasma. The transition concentrations  and depend on solute type and the polar solvent type. Typically ~10-6 M<<~10-4 M and  < < . CDplasma and IPDplasma are composed of few solvated solutes and numerous polar solvent molecules — these domains are not micelles c. CDplasma and IPDplasma are very stable domains. Energy gained by a solute on incorporation in IPDplasma is larger than that of CDplasma (few eV), implying this difference underlies solvation of difficult soluble compounds for . The solvated solute molecules within IPDplasma are crystalline-ordered, with the polar solvent molecules symmetrically aligned around their nearest neighbor solute molecule (see Figure 3b). i.e., the liquid IPDplasma have a crystalline structure. CDplasma’s solvated solute molecules and their non-solvation shell solvent molecules locate randomly (see Figure 3a).

For a CDplasma, the plasma oscillations of its identical solvated solute molecules are coherent, resonating in phase with the coherently condensed photons mediating their interactions (Del Giudice et al., 2000). For an IPDplasma, the plasma oscillations of its identical solvated solute molecules are in-phase, resonating in phase with the in-phase condensed photons mediating their interactions (Yinnon and Yinnon, 2012).  

For the diameter of CDplasma holds: vCDplasma ≈1/v CDplasma. For monovalent electrolytes, vCDplasma=7.4×103(mp/mi)1/2C 3/4 GHz is the frequency of EFM mediating the attractive interactions between identical solvated solute molecules, with mi and mp, respectively, the mass of the ion and the proton. The expression of vCDplasma results from C influencing a counter-ion mean charge density distribution , with: denoting the Debye length, ε  is the dielectric constant, and e the charge of the electron. LD equals the distance beyond which the Coulomb electric field around a solute molecule is at any instant fully screened by all its neighboring solvent molecules. For solutions containing non-monovalent ions or non-electrolytic solutes, vCDplasma resembles the aforementioned expression, but is solute type dependent. The expressions for vCDplasma connote that on dilution the diameter of CDplasma increases, the number of CDplasma’s solvated solute molecules diminishes and that of its solvent molecules enhances.At C=, LD equals the distance between closest neighbor’s identical solute molecules. This distance is proportional to C-1/3. For C>, LD is smaller than this distance. For C≤, LD is larger than this distance. Thus for C≤, solvated solute molecules in CDplasma start experiencing the repulsive Coulomb interactions with their identical nearest neighbors. Therefore on diluting below , it is energetically unfavorable the number of solute molecules in IPDplasma () and the frequency of their plasma oscillations decreases and the diameter of IPDplasma increases. In other words at C≤: the frequency of IPDplasma’s solutes’ plasma oscillations and the diameter of IPDplasma have values determined respectively, by vCDplasma for C= and  = x with  the volume of the domains at . The aforementioned implies that on diluting solutions below , the number of IPDplasma diminishes.

 

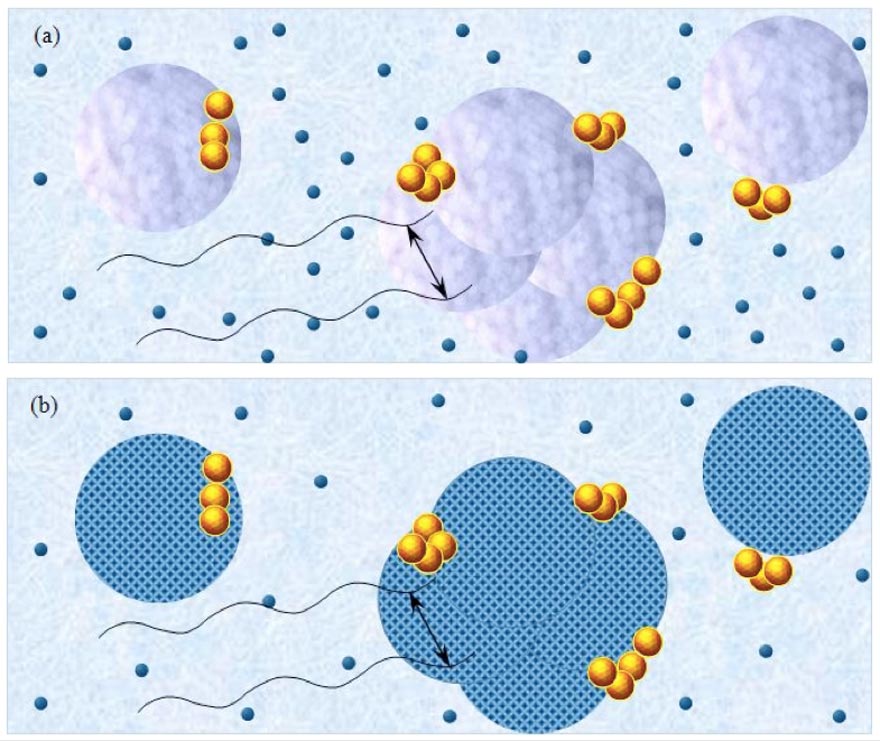
Figure 5a-b: Schematic pictures of polar liquids containing solvated solutes. Figure (a) pertains to CIPDplasma<C<CCDplasma with purple-blue colored balls and their agglomerates representing, respectively, ~10-6 m CDplasma and supra-CDplasma. Figure (b) pertains to C<CIPDplasma, with blue-crystalline structured balls and their agglomerates representing, respectively,  the ~10-6 m crystalline structured IPDplasma and supra-IPDplasma. Tiny dark-blue balls represent ~10-9 m solvated solutes with their hydration shells — these randomly move in the interstices between the domains. Yellow-brown balls and their agglomerates represent, respectively, ~10-7 m and supra-, which are stabilized by CDplasma or IPDplasma. Black cosine curves represent THz to MHz EMF facilitating interactions (symbolized by black double arrows) among the solvated solutes organized in CDplasma or IPDplasma. These interactions span ~10-6 m. Sizes of the domains and solvated solutes are not presented according to their realistic scale ratios.

 

CDplasma and IPDplasma may stabilize CDelec at their borders. Stabilization only occurs at the borders, because CDelec cannot contain solutes. A schematic picture of a polar liquid with solutes  at <C<, i.e., wherein part of the solute molecules are organized in CDplasma, is presented in Figure 5a. A similar picture but for C<, i.e., a solution wherein part of the solute molecules are organized in IPDplasma, is presented in Figure 5b.

Concentration ranges for CD formation —

The abovementioned transition concentrations , and delineate C ranges for formation of, respectively, CDrot, CDplasma and IPDplasma. Their theoretical underpinnings vary greatly.

  • Solvent molecules coherently oscillating between two of their rotational states is crucial for their organization in CDrot. Solutes affect these oscillations. In the presence of few solutes, the rotational states of the solvent molecules get only slightly perturbed and the coherence persists. However, numerous solutes destroy the coherence (Del Giudice and Vitiello, 2006). Therefore CDrot only form for C<.
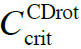  • Coherence of the plasma oscillations of solvated solute molecules sets in only below a solute type dependent C, i.e.,  –– see Del Giudice et al. (2000)  Eq. 14. The coherence is crucial for CDplasma formation.
  • In phase plasma oscillations of solvated solute molecules set in when nearest neighbor molecules experience their Coulomb interactions, i.e., when their intermolecular distance is less than the Debye length — a condition satisfied for C< 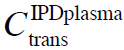(Yinnon and Yinnon, 2012). These in phase oscillations are crucial for IPDplasma formation.
  • H2O coherently oscillating between their electronic ground state and an excited state is crucial for their organization in 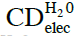. Due to energetic reasons solutes cannot penetrate into 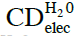. Thus formation of 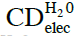is independent of C.

 

Superfluidic CD —

CDrot, IPDplasma and are superfluidic domains (Bono et al., 2012; Del Giudice et al., 2013; Yinnon and Yinnon, 2012), i.e., their molecules do not collide. A single collision would destroy their coherence.  CDplasma are not superfluidic — their coherent oscillating solvated solute molecules and hydration shells’ solvent molecules do not collide but their non-hydration solvent molecules do collide. Solvent molecules neither included in CD nor in solvated solutes’ hydration shells move randomly and collide; so do solvated solute molecules not included in CDplasma or IPDplasma.

As to the impact of CD colliding with the randomly moving molecules located in their interstices: when the collision energy is larger than the energy a molecule gains by its inclusion in CD, a molecule may desorb from the CD. The superfluidity implies that collisions excite the whole CD. For example, as in superfluidic Helium, whirlpools (so called rotons or vortexes) may be created. These excited CD states also may be induced by stirring or irradiation. When an excites state’s energy is less than the energy a molecule gains by its inclusion in CD, it persists for macroscopic times. Hence CD constitute “long-term information storage devices”. The superfluidity of CD has implications for the liquid’s properties, e.g., electric conductivity.

Fractions of molecules included in CD —

Fractions of solvent molecules included in CDrot, in CDelec, in IPDplasma or CDplasma, and fractions of solvated solutes included in CDplasma or IPDplasma depend on temperature, concentration and solute type (Preparata 1995 chapter 10; Del Giudice et al., 2000; Yinnon and Yinnon, 2012).

 

Discussion

Experimental data conforming to some predictions of the QED model for polar liquids and their solutions have been discussed in various publications. A detailed review of these is outside the scope of this paper, although indeed called for. Here we suffice with citing some relevant papers. 

In their seminal publications predicting presence of CDrot, CDelec and CDplasma in aqueous systems, Del Giudice et al. (1988, 2000) and Arani et al. (1995) showed these clarify various phenomena which for many decades were unexplainable with the customary electrostatic models, e.g., some of the so called anomalies of water. Yinnon and Yinnon (2009) point to significant experimental data in the literature pertaining to domains in aqueous solutions which have properties conforming to those of CDrot, and CDplasma. Since 2009 additional experimental data corroborating the presence and properties of these domains has accumulated — see for example Del Giudice et al., 2010, 2013; De Ninno and Congiu Castellano, 2011; De Nino et al., 2013; Germano et al., 2013; Liu et al., 2011, 2012; Yinnon and Yinnon, 2011; Yinnon and Elia, 2013; Elia et al., 2015; Yinnon et al., 2015c. Identification of IPDplasma and their properties, together with analyses of some experimental data verifying these, were carried out by Yinnon and Yinnon (2012).

For all CD types, analyzed experimental data mainly concern their dynamics, their impact on the liquid’s physicochemical properties and some of their structural aspects. As to the effects of EMF on CD, hitherto the related measurements have not been analyzed in depth, and the effects only have been inferred (Montagnier et al., 2009; Yinnon and Yinnon, 2011; Yinnon and Elia, 2013).

 

Conclusions

This paper relates on the structure of polar liquids and their solutions. The quantum electrodynamics (QED) theory’s predictions for the structure of these liquids considerably differ from those of the customary electrostatic theories. While the former explicitly describe the electrodynamic interactions mediated by EMF, the latter assume that these interactions can be treated as small perturbations or ignored. Since the former shows that electrodynamic interactions under certain conditions induce phase transitions leading to formation of coherence domains, the limits of the customary theories have to be carefully assessed. Hitherto, only few assessments were undertaken. These mainly focus on the domains’ dissipative dynamics and their impact on the liquid’s physicochemical properties.

A detailed review of these assessments is called for – in particular it is needed to map the many challenging research projects still required for verifying numerous aspects of polar liquids predicted by QED. However, even now it is overt that QED analyses are required for a series of experimental data published since 2008 pertaining to direct observation of domains in polar liquids and the effects of EMF on these, e.g., for liquids perturbed by serial dilutions or immersion of membranes [for reviews of the data see Konovalov and Ryzhkina (2014b) and Elia et al. (2015)]. As to the liquids perturbed by membranes, some QED analyses are presented in Del Giudice et al. (2010, 2013) and Yinnon et al. (2015c). As to serial diluted solutions, analyses of their directly observed domains and the impact of EMF, these are the foci of the following papers in this journal’s volume (Yinnon and Liu, 2015a and 2015b).

Though the aforementioned stresses the need for gathering additional experimental data supporting the predictions of the QED model, it should be emphasized that additional theoretical work is required too. Hitherto only a few properties of polar liquids resulting from their electrodynamic interactions have been derived. For example, a mathematical expression for the critical concentration below which CDrot form is still lacking. Also the derivation of quantitative expressions for physicochemical variables of polar liquids containing CD, e.g., their electric conductivity, dielectric permittivity and surface tension, are important challenges ahead. Detailed predictions on the excited states of the various CD and their influence on spectra of polar liquids also has to be addressed in future research projects.

 

Acknowledgements

With much appreciation we thank Prof. A. I. Konovalov for his many helpful discussions, his careful reading of the manuscript and his detailed constructive comments. Tamar Yinnon expresses her gratitude to Prof. A. M. Yinnon for his continuous support and encouragement. She also thanks Dr. A. De Ninno and Dr. Z. Kirson for helpful discussions pertaining to the history of modeling quantum fluctuations. She also thankfully acknowledges the valuable discussions with Prof. N.P. Pal’mina and her technical support. Z.-Q. Liu thankfully acknowledges the support of the National Natural Science Foundation of China (No. 11302118), Natural Science foundation of Shandong Province (No. ZR2013AQ015) and the Science Foundation of Qufu Normal University (No. BSQD2012053).

 


Table 1: List of abbreviations in alphabetic order, followed by Greek symbols abbreviations.

 

References

Apostol, M (2009). Coherence domains in matter interacting with radiation. Phys Lett A 373: 379-384.

Arani R, Bono I, Del Giudice E; Preparata G (1995). QED coherence and the thermodynamics of water. Int J Mod Phys B 9: 1813-1841.

Bialynicki-Birula I, Rzazewski K (1979). No-go theorem concerning the superradiant transition in atomic systems. Phys Rev A 19: 301-303 and references therein.

Bono I, Del Giudice E, Gamberale L, Henry M (2012). Emergence of the Coherent Structure of Liquid Water. Water 4: 510-532.

Casimir HBG (1948). On the attraction between two perfectly conducting plates. Proc Kon Nederland Akad Wetensch B51: 793–795.

Casimir HBG, and Polder D, (1948). The Influence of Retardation on the London-van der Waals Forces. Phys Rev 73: 360–372.

De Ninno A, Congiu Castellano A (2011). Co-ordination of water molecules in isotopic mixtures. J Mol Struct 1006: 434-440.

De Ninno A, Congiu Castellano A, Del Giudice E (2013). The supramolecular structure of liquid water and quantum coherent processes in biology. J Phys: Conf Ser 442: 012031 pp 1 – 9.

Del Giudice E, Prepara G, Vitiello G (1988). Water as a free electric dipole laser. Phys Rev Lett 61: 1085-1088.

Del Giudice E, Mele R, Preparata G (1993). Dicke Hamiltonian and Superradiant Phase Transitions. Mod Phys Lett B 7:1851-1855.

Del Giudice E, Preparata G (1998). “A new QED picture of water”, in Macroscopic Quantum Coherence, eds. Sassaroli E, Srivastava YN, Swain J, Widom A (World Scientific, Singapore).

Del Giudice E, Preparata G, Fleischmann M ( 2000). QED coherence and electrolyte solutions. J Electroanal Chem 482: 110–116.

Del Giudice E, Vitiello G. (2006). Role of the electromagnetic field in the formation of domains in the process of symmetry-breaking phase transitions. Phys Rev A 74: 022105-1-022105-9.

Del Giudice E (2007). Quantum Field Theory applied to the water structure. Summer School 2007 of the International Institute of Biophysics Neuss Germany.

Del Giudice E, Spinetti PR and Tedeschi A (2010). Water dynamics at the root of metamorphosis in living organisms. Water 2: 566-586.

Del Giudice E, Tedeschi A, Vitiello G, Voeikov VL (2013). Coherent structures in liquid water close to hydrophilic surfaces. J Phys: Conf Ser 442: 012028.

Dicke RH (1954). Coherence in spontaneous radiation processes. Phys Rev 93:99-110.

Dzyaloshinskii, E; Lifshitz EM; Pitaevskii LP (1961). The general theory of van der Waals forces. Usp Fiz Nauk 73, 381 (1961); English translation: Dzyaloshinskii, I. E., Lifshitz, E. M. & Pitaevskii, L. P. (1961). Adv Phys 10, 165–209.

Elia V, Niccoli M (1999). Thermodynamics of Extremely Diluted Aqueous solutions. Ann New York Acad Sci 870: 241-248.

Elia V, Niccoli M (2000). New Physico-chemical properties of water induced by mechanical treatments: A calorimetric study at 25ºC. J Therm Anal Cal 61: 527-537.

Elia V, Niccoli M (2004a). New Physico-chemical properties of extremely diluted aqueous solutions. J Therm Anal Cal 75: 815-836.

Elia V, Napoli E, Niccoli M, Nonatelli L, Ramaglia A, Ventimiglia E (2004b). New Physico-chemical properties of extremely diluted aqueous solutions. A calorimetric and conductivity study at 25°C. J Therm Anal Cal 78: 331–342.

Elia V, Marrari LA, Napoli E (2012). Aqueous nanostructures in water induced by electromagnetic fields emitted by EDS: A calorimetric study of fullerene and carbon nanotube EDS. J Therm Anal Cal 107: 843-851.

Elia V, Germano R, Napoli E, (2015). Permanent Dissipative Structures in Water: The Matrix of Life? Experimental Evidences and their Quantum Origin. Curr Top Med Chem 15: 559-571.

Emary C, Brandes T (2003). Chaos and the quantum phase transition in the Dicke model. Phys Rev E 67: 066203-066225.

Germano R, Del Giudice E, De Ninno A, Elia V, Hison C, Napoli E, Tontodonato V, Tuccinardi FP, Vitiello G (2013). Oxhydroelectric effect in bi-Distilled Water. Key Eng Maters 543: 455-459.

Hepp K, Lieb EH (1973a). On the Superradiant Phase Transition for Molecules in a Quantized Radiation Field: the Dicke Maser Model. Ann Phys 76: 360-404.

Hepp K, Lieb EH (1973b). Equilibrium statistical mechanics of matter interacting with the quantized Radiation field. Phys Rev A 8: 2517-25.

Ho M-W (2014). Large Supramolecular Water Clusters Caught on Camera – A Review. WATER Journal 6: 1-12.

Horne RA (1971). Water and Aqueous Solutions: Structure, Thermodynamic and Transport Processes. Wiley-Interscience New York. Chapters 8-12.

Iitaka T (2010). Stability of ferroelectric ice. arXiv:1007.1792v1 cond-mat.mtrl-sci.

Konovalov AI, Ryzhkina IS, Murtazina LI, Timosheva AP, Shagidullin RR, Chernova AV, Avvakumova LV, Fattakhov SG (2008). Supramolecular systems based on the melamine salt of bis(hydroxymethyl)phosphinic acid (melafen) dihydrate and surfactants 1. Structure and self-association in water and chloroform. Izv Akad Nauk Ser Khim 1207–1214; Russ Chem Bull Int Ed. 57: 1231-1238.

Konovalov AI (2013). The formation of nanosized molecular ensembles in highly dilute aqueous solutions. Herald of the Russian Academy of Sciences, 83: 513–519.

Konovalov AI (2014a). Nano assoicates: Terra incognita. Science in Russia 199: 1-10.

Konovalov AI, Ryzhkina IS (2014b). Reviews: Formation of nanoassociates as a key to understanding of physicochemical and biological properties of highly dilute aqueous solutions. Russ Chem Bull Int Ed 63: 1-14.

Konovalov AI, Mal’tseva EL, Ryzhkina IS, Murtazina LI, Kiseleva YuV, Kasparov VV, Pal’mina NP (2014c). Formation of nanoassociates is a factor determining physicochemical and biological properties of highly diluted aqueous solutions. Dokl Phys Chem 456: 86-89.

Liu ZQ, Li YL, Zhang GC, Jiang SR (2011). Dynamical mechanism of the liquid film motor. Phys Rev E 83:026303-1 to 026303-7.

Liu ZQ, Zhang GC, Li YL, Jiang SR (2012). Water film motor driven by alternating electric fields: Its dynamical characteristics. Phys Rev E 85:036314 -1 to 036314 -12.

Lo S-Y (1996). Anomalous state of ice. Mod Phys Lett 10: 909-919.

Lo S-Y, Geng XU, Gann, D (2009). Evidence of stable-water-clusters at room temperature and normal pressure. Phys Lett A 373: 3872 -3876.

London, F (1930). On the theory and system of molecular forces. Zeitschrift für Physik, 63: 245-279. English translations in H. Hettema, Quantum Chemistry, Classic Scientific Paper London (1930), Classic Scientific Papers, World Scientific, Singapore (2000), p 369-399.

Montagnier L, Aïssa J, Ferris S, Montagnier JL, Lavallee C (2009). Electromagnetic signals are produced by aqueous nanostructures derived from bacterial DNA sequences. Interdiscip Sci Comput Life Sci 1: 81–90.

Montagnier L, Aïssa J, Del Giudice E, Lavallee C, Tedeschi A, Vitiello G (2011). DNA waves and water. J Phys: Conf Ser 306: 012007.

Pal’mina NP, Mal’tseva EL, Kurnakova NV, Burlakova EB (1994). Effect of α-Tocopherol over a Wide Concentration Range (10-17-10-2M) on Protein Kinase C. Biochimiya (Russian) 59: 193-200.

Preparata G (1988). Quantum field theory of the free electron laser. Phys Rev A 38: 233-237.

Preparata G (1995). QED Coherence in Matter. World Scientific, Singapore, New Jersey, London, Hong Kong.

Ryzhkina IS, Murtazina LI, Kiseleva YuV, Konovalov AI (2009). Properties of Supramolecular nanoassociates formed in aqueous solutions of biologically active compounds in low or ultra-low concentrations. Dokl Phys Chem 428: 196–200.

Ryzhkina IS, Murtazina LI, Academician Konovalov AI (2011). Action of the external electromagnetic field is the condition of nanoassociate formation in highly diluted aqueous solutions. Dokl Phys Chem 440: 201–204.

Sivasubramanian S, Widom A, Srivastava YN (2001). Gauge invariant formulations of Dicke–Preparata super-radiant models Physica A 301 :241-254.

Ibid (2002). Landau ghosts and anti-ghosts in condensed matter and high density hadronic matter. Mod Phys Lett B 16:1201-1209.

Ibid (2003) Microscopic basis of thermal superradiance. J Phys Condens Matter 15: 1109-1118.

Sivasubramanian S, Widom A, Srivastava YN (2005). The Clausius–Mossotti phase transition in polar liquids. Physica A 345: 356 -366.

Yinnon CA, Yinnon TA (2009). Domains in aqueous solutions: theory and experimental evidence. Mod Phys Lett 23: 1959-1973.

Yinnon TA, Yinnon CA (2011). Electric dipole aggregates in very dilute polar liquids: Theory and experimental evidence. Int J Mod Phys B 25: 3707-3743.

Yinnon TA, Yinnon CA (2012). Domains of solvated ions in aqueous solutions, their characteristics and impact on electric conductivity: theory and experimental evidence. Mod Phys Lett 26: 1150006-1 to 1150006-14.

Yinnon TA, Elia V (2013). Dynamics in perturbed very dilute aqueous solutions: theory and experimental evidence. Int J Mod Phys B 27:1350005-1 to 1350005-35.

Yinnon TA and Liu Z-Q (2015a). Domains formation mediated by electromagnetic fields in very dilute aqueous solutions: 2. Analyses of experimental data on solutions of strong electrolytes. WATER Journal 7: 48-69.

Yinnon TA and Liu Z-Q (2015b). Domains formation mediated by electromagnetic fields in very dilute aqueous solutions: 3. Analyses of experimental data on solutions of weak electrolytes and non-electrolytes. WATER Journal in Press.

Yinnon TA, Elia V, Napoli E, Germano R, Liu ZQ (2015c). Water ordering induced by interfaces: an experimental and theoretical study. WATER Journal in Press. 

Close Menu