Nanostructures of Water Molecules in Iteratively Filtered Water
Elia V1, Marchettini N2*, Napoli E1 and Tiezzi E°
1Department of Chemistry, University “Federico II” of Naples, Complesso Universitario, di Monte S’Angelo, Via Cintia, 80126 Naples, Italy
2Ecodynamics Group, Department of Earth, Environmental and Physical Sciences, University of Siena, Pian dei Mantellini, 44, 53100 Siena, Italy
ºEnzo Tiezzi passed away on June 25th, 2010. The authors thank Enzo for his precious ideas and suggestions, which are at the basis of this paper.
*Correspondence E-mail: nadia.marchettini@unisi.it
Key Words: Pure water; conductometry; densitometry; dissipative structures; aqueous nanostructures; filtration.
Received Aug 30th 2015; Revised Feb 11th, 2016; Accepted March 18th; Published April 20th; Online May 15th, 2016
Abstract
Here we present experimental results on the physico-chemical properties (electrical conductivity and density) of pure, twice distilled water, subjected to iterative filtration through Pyrex glass filters (Büchner funnels). Because of the linear correlation between conductivity and calorimetry measures, all the phenomena highlighted by conductivity measurements are also highlighted by calorimetric measurements. After iterative filtration, electrical conductivity increased by two orders of magnitude and density showed variations in the fourth decimal digit. The results highlight the importance of the number of iterations, the dimension of filter pores and the volume of filtered water. Part of the increase (10-30%) may be attributed to impurities released by the glass filters. The hypothesis is that the remaining 70-90% of the increment comes from variations in the supramolecular structure of water. The iterative filtration procedure involves flows of energy and matter in an open system. The energy flux is partially dissipated as heat, permitting formation of dissipative structures. The structured water (exclusion zones) at the interface between the glass pores and the liquid probably also plays a major role in determining the formation of dissipative structures. Water, the main ingredient of living systems, exhibits extraordinary self-organization potential triggered by several kinds of perturbation, including mechanical ones.
Article Outline
Introduction
Papers on water and aqueous solutions are increasingly featured in the scientific literature (Lo SY et al., 1996; Gregory et al., 1997; Wourtersen et al., 1997; Mishima and Stanley, 1998; Elia and Niccoli, 1999; Lobyshev et al., 1999; Woutersen and Bakker, 1999; Elia and Niccoli, 2000; Robinson et al., 2000; Ropp et al., 2001; Errington and Debenedetti, 2001; Kropman and Bakker, 2001; Samal and Geckeler, 2001; Lobyshev et al., 2003; Rey, 2003; Elia and Niccoli, 2004; Bakker et al., 2005; Malescio et al., 2005; Elia et al., 2006; Ball, 2008; Montagnier et al., 2009; Lo SY et al., 2009; Elia and Napoli, 2012; Elia et al., 2013a). “No one really understands water. It is embarrassing to admit it, but the stuff that covers two-thirds of our planet is still a mystery. Worse, the more we look, the more the problems accumulate: new techniques probing deeper into the molecular architecture of liquid water are throwing up more puzzles,” wrote P. Ball (2008) in Nature. The idea of water as a system capable of self-organization triggered by various perturbations (mechanical and/or electromagnetic) is gaining momentum. Many of the properties shown by these new studies on water are not currently explained in terms of classical thermodynamics and quantum mechanics, but by thermodynamics of far-from-equilibrium systems (Prigogine, 1977; Nicolis, 1989; Popescu, 2003; Sanduloviciu et al., 2005; Chiriach, 2006). Coherent quantum electrodynamics (Marchettini et al., 2010) may open up new ways of investigating these novel results. It is reasonable to say that although water is by far the most studied liquid, it is not yet sufficiently understood.
Our past studies on the physico-chemical properties of extremely diluted solutions (EDS) or ultra-molecular dilutions showed that pure water has extraordinary properties. We investigated the physico-chemical variations of water caused by aging small volumes (less than 10 ml) for periods of the order of tens of months. During these experiments, we witnessed sporadic cases of mould formation in the liquid, caused by non-sterile systems and the occasional presence of traces of organic substances. In order to prevent contributions by contaminants to the physico-chemical parameters we were measuring, the solutions were filtered with filter pore sizes ranging from 0.45 to 0.022 μm. The electrical conductivity (μS cm-1) of the clear filtrate was systematically higher than that of the initial solution, often by a large margin. The importance of filtration in the formation of “aqueous nanostructures” was recently highlighted by Luc Montagnier (Nobel laureate in Medicine, 2008) (Montagnier et al., 2009).
Despite their profoundly different nature, the linear correlation between electrical conductivity and density suggests that a single cause underlies the observed changes in these parameters. In fact, electrical conductivity is linked to the transport of electric charges under a gradient of electric potential, while density is linked to bundling of water molecules in the liquid phase. The hypothesis that iterative procedures involving flows of energy and matter in an open system may lead to the formation of dissipative structures or nanostructures of water molecules was confirmed by recent experimental results (Lo, 1996; Elia and Napoli, 2010; Elia and Napoli, 2012; Elia et al., 2013; Yinnon and Elia, 2013; Capolupo et al., 2014; Elia et al., 2014a, Elia et al., 2014b). In liquid phase, UV-vis spectra showed an absorption peak at 275 nm while the FT-IR remained substantially unvaried with respect to untreated water. Lyophilized samples gave solid residues whose nature was investigated by IR spectroscopy. For atomic force microscopy (AFM), liquid samples were evaporated on mica holders at room temperature and pressure. The emerging pictures suggested that physical perturbations having low energy content can promote unexpected self-organization in liquid water that survives evaporation or lyophilisation, forming a solid phase stable at room temperature and pressure.
The aim of this paper is to focus on water iteratively filtered with sintered glass filters. In the liquid phase, these techniques were employed: pH, electrical conductivity, calorimetric and spectroscopic measurements in IR and UV-vis range. In the solid phase we employed these other techniques: Atomic Force Microscopy (AFM) and IR spectra of lyophilized samples. The fact that different approaches showed unexpected agreement despite the fact that they started from parameters of different physical and chemical nature is somewhat revolutionary with respect to classical chemistry and thermodynamics. According to Montagnier, these phenomena illustrate the thermodynamics of far-from-equilibrium systems, conceived by Nobel laureate Ilya Prigogine, and the formation of dissipative structures explains anomalies evident after long periods of time, as well as apparent anomalies stemming from the use of small volumes. Time is of paramount importance in Prigogine’s dissipative structures (Prigogine, 1977; Nicolis, 1989). Hopefully a crossroad can be found, where the points of view on kinetic, thermodynamic and quantum electrodynamic theories converge. A growing body of data, obtained by diverse and unrelated methods, shows that only a unified interpretation that takes these different, yet converging approaches into account can explain and harmonize these novel behaviours of water. In fact, a phenomenon where time (Prigogine’s view) and interfaces with interactions in confined environments play a role may help create a bridge between the thermodynamics of far-from-equilibrium systems and the chemistry of interfaces, so that classical physical chemistry can incorporate the formation of dissipative structures, on one hand, and the formation of water structures, on the other, and maybe even the possibility of “solid” formations (Yinnon and Elia, 2013; Elia et al., 2013c; Capolupo et al., 2014: Elia et al., 2014a; Elia et al., 2014b) that are currently a most unorthodox hypothesis. The idea of water and aqueous solutions as systems capable of self-organization triggered by various perturbations (mechanical and/or electromagnetic) is gaining momentum.
Experimental Background
The iterative filtration of a given volume (1-30 ml) of twice distilled water simply consists in: vacuum-filtering the liquid, recovering the filtrate and repeating the filtration step. This is repeated up to 250 times. The following filters were used in a preliminary study of the effects of iterative filtration:
a. disposable filters (Millipore) made of cellulose acetate, with porosities of 0.45, 0.22 and 0.025 μm;
b. ceramic filters (pot filters);
c. glass filters (Büchner funnels) with porosity between 90 and 5 μm: R1 = 90-120 μm, R2 = 40-90 μm, R3 = 15-40 μm, R4 = 5-15 μm and R5 = 1-5 μm.
The preliminary study showed that the qualitative effects on water were the same regardless of the filter type. After assessing the repeatability of the phenomenon, it was decided to use only Pyrex glass (Büchner) filters. Considering the novelty of the endeavour, we focused on impurities released by glass containers and filters that could affect electrical conductivity and density. The main chemical impurity is alkaline oxide (Na2O) released by glass. In contact with water, it is transformed into sodium hydroxide (NaOH) and in contact with atmospheric carbon dioxide (CO2), sodium hydroxide turns into sodium bicarbonate (NaHCO3). We therefore systematically determined the sodium concentrations of samples and subtracted the contribution of sodium bicarbonate from the conductivity readings. The concentrations of impurities derived from other components of glass (SiO2, B2O3 and Al2O3) were very low compared to sodium bicarbonate and did not contribute significantly to electrical conductivity at the low alkalinity of water, or to density (see Table 9).
Methods
Conductivity measurements – Systematic measurements of specific conductivity were performed on the samples, using a YSI 3200 conductometer with a conductivity cell having a constant of 1.0 cm-1. Before measuring the conductivity of a sample, the cell was calibrated by determining the cell constant K (cm-1). The specific conductivity, χ (μS cm-1), was then obtained as the product of the cell constant and the conductivity of the solution. For a given conductivity cell, the cell constant was determined by measuring the conductivity of a KCl solution with a specific conductivity known with great accuracy, at several concentrations and temperatures. All conductivities were temperature corrected to 25°C, using a pre-stored temperature compensation for pure water (Ball, 2008).
Density measurements – The solution densities were measured using a vibrating-tube digital densimeter (model DMA 5000 by Anton Paar, Austria) with a precision of ±1·10-6 g·cm-3 and an accuracy of ±5·10-6 g·cm-3. The temperature of the water around the densimeter cell was controlled to ±0.001 K. The densimeter was calibrated periodically with dry air and pure water.
Analytical determination of impurities – The concentration of sodium was determined by atomic absorption spectrometry using a Varian Spectra A instrument. Before sample measurement, a calibration curve was obtained using standard solutions of NaCl in water and diluted to 1 liter to obtain 1000 µg/mL of Na. The working conditions were: 5 mA lamp current; acetylene fuel; air support; oxidizing flame stoichiometry. The wavelength depended on the concentration range of sodium. For our samples it was 589.6 nm. Sodium is partially ionized in the air-acetylene flame. To suppress ionization, some potassium chloride solution was added to produce a final concentration of 2000 µg/mL in all solutions, including the blank. Impurities were in the ppm range. Si, Al and B concentrations were determined by the ICP-mass method using an Agilent 7500 ICP-MS instrument.
Results and Discussion
Table 1 reports the volume of the Milli-Q water samples subjected to iterative filtration, the number of iterations (N) and measured electrical conductivity, χ (μS cm-1) and Büchner filter type (R1-R5). Table 2 reports the volume of Milli-Q water samples subjected to iterative filtration, the number of iterations (N) and measured electrical conductivity, χ (μS cm-1), sodium bicarbonate concentrations [Na+] (mol L-1×105) and Büchner filter type (R4). When the number of iterations increased, the specific electrical conductivity and density always increased. The conductivity and density of filtered samples always increased as time flows.
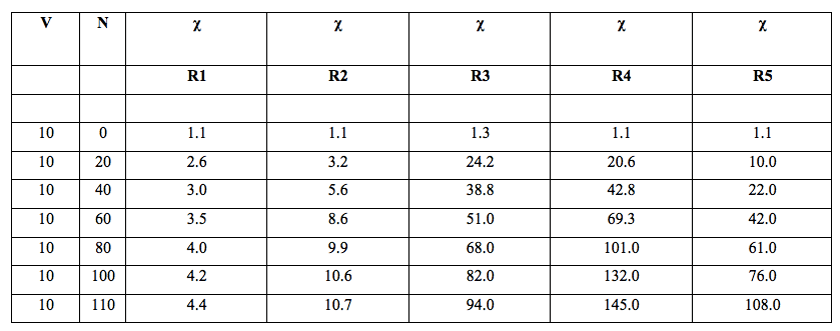
Table 1: Volume of Milli-Q water filtered, V (mL), number of filtrations, N and specific electrical conductivity, χ (µS cm-1) of the water samples after filtrations with filters of decreasing porosity, R (µm): R1 (90-150 µm), R2 (40-90 µm), R3 (15-40 µm), R4 (5-15 µm), R5 (1-5 µm).
We discovered that the increase in electrical conductivity depended on:
1. number of filtrations
2. filter pore size
3. volume of filtered water.
To have information on the role of the three variables we fixed for example the dimensions of the pores and the volume. Then we increased the number of filtrations. Conductivity increased. The speed of the increase (the slope of the quasi linear trend of conductivity versus number of filtrations) depended on the volume used: the smaller the volume filtered, the steeper the slope of the linear trend. To show this relation we changed the volume from 30 to 12 ml after 80 filtrations and then from 12 to 10 (after 140 filtrations) and to 5 ml after 180 filtrations (Table 2). These changes in volume of the filtered samples coincided with significant increases in slope. The change in volume was obtained simply by extracting the necessary quantity of liquid from the sample to obtain the new volume. The extracted volume was used in the normal way for the analytical tests. In each of these experiments the pores of the used filter is R4. These two reported experiments are only examples of large ones.
1. In all these experiments, the conductivity increased with the number of filtrations.
2. The smaller the sample volume, the steeper the slope of the quasi linear trend of conductivity vs. number of filtrations.
3. Conductivity showed a non linear trend with respect to filter pores size (R1 to R5).
Table 2 shows the concentration of Na+ at various numbers of filtrations. The concentrations increased with number of filtrations, as expected. An increase in chemical impurities would not explain this increase in conductivity.
![Table 2: Volume of Milli-Q water filtered, V (mL), number of filtrations, N, with R4 filter (pore size 5-15 µm), specific electrical conductivity, χ (µS cm-1) and concentration of sodium bicarbonate impurities [Na+] (mol L-1×105) released by the glass container.](/uploads/vol7/elia/Table-2.png "Table 2: Volume of Milli-Q water filtered, V (mL), number of filtrations, N, with R4 filter (pore size 5-15 µm), specific electrical conductivity, χ (µS cm-1) and concentration of sodium bicarbonate impurities [Na+] (mol L-1×105) released by the glass container.")
Table 2: Volume of Milli-Q water filtered, V (mL), number of filtrations, N, with R4 filter (pore size 5-15 µm), specific electrical conductivity, χ (µS cm-1) and concentration of sodium bicarbonate impurities [Na+] (mol L-1×105) released by the glass container.
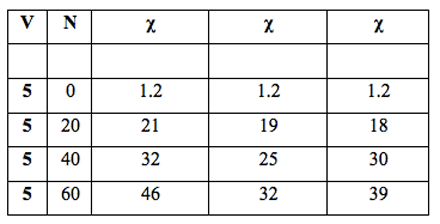
Table 3: Volume of three Milli-Q water samples filtered, V (mL), number of filtrations, N, with R4 filter (pore size 5-15 µm) and specific electrical conductivity, χ (µS cm-1).
The relationship between electrical conductivity and number of filtrations also varied with filter pore size (see Table 1 and Figure 1).
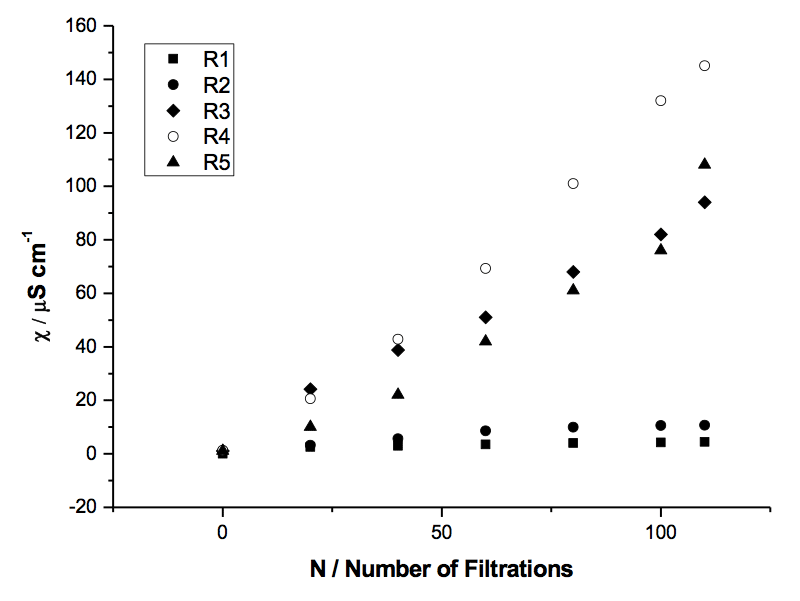
Figure 1: Specific electrical conductivity of samples of Milli-Q H2O filtered with 5 filters of decreasing porosity R (µm): R1 (90-150 µm), R2 (40-90 µm), R3 (15-40 µm), R4 (5-15 µm), R5 (1-5 µm).
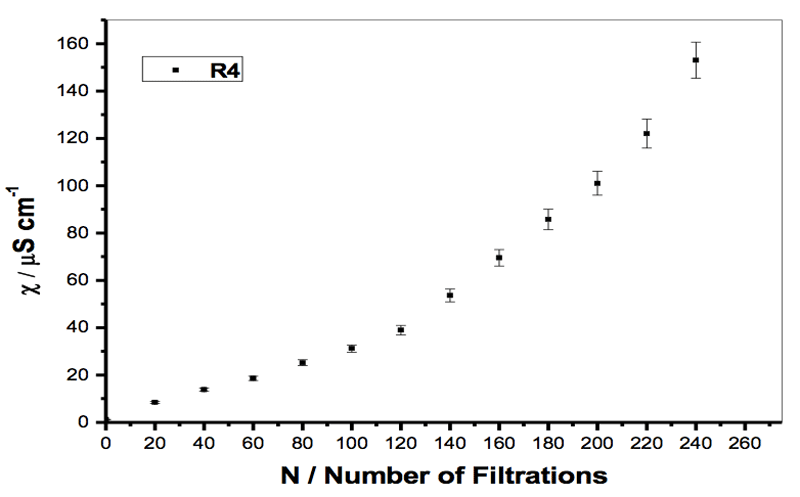
Figure 2: Specific electrical conductivity of a sample of Milli-Q water filtered with filter R4 (5-15 µm), when the initial volume of the sample was reduced from 30 to 5 mL (see Table 2).
The phenomenon was repeatable but not reproducible, i.e. the measured values varied with the experiment. The experimental data suggests that the iterative filtrations modified the physico-chemical properties of the water. For all filter types there was also a significant “volume effect” (Elia et al., 2006), whereby the increase in specific conductivity for each iteration step was greater for small sample volumes (see Table 2 and Figure 2). In fact, the roughly linear trends of χ against number of iterations, for a constant volume of filtered water, showed very different slopes that were steeper for smaller volumes. We calculated the standard deviation on a single experiment by measuring the conductivity of a sample of about 42 μS cm-1 ten times. The mean value was 42.0 μS cm-1 and the standard deviation 0.1 μS cm-1 (0.24% of the mean value). For density measures we found a standard deviation of 2×10-6 g cm-3. In Figures 2-4, the error bar is estimated in excess (5%), from the sensitivity of the instrument.
It can be seen that χ increased systematically with the number (N) of iterations in relation to the following parameters: number of filtrations, filter pore size and sample volume. Table 4 shows specific conductivity χ and the difference between the density d of filtered samples and the density d0 of unfiltered water, for samples the density of which was measured.
We compared the repeatability of the phenomenon by employing the same filter in three experiments with equal sample volumes. A comparable number of filtrations was carried out in these experiments. The results are reported in Table 3 and Figure 3.
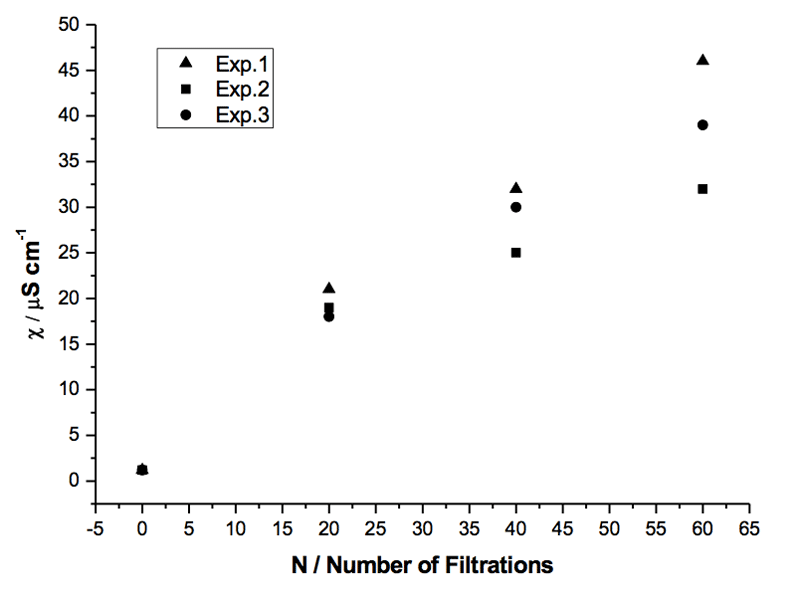
Figure 3: Specific electrical conductivity of three samples of Milli-Q water (volume 5 mL each) subjected to the same number of filtrations with the same filter R4 (5-15 µm) (see Table 3).
Table 5 reports the specific electrical conductivity of the filtered Milli-Q water, the number of filtrations, the density of the samples filtered with R4 filters (pore size 5-15 μm), and the concentration of impurities released from the glass [Na+], [B], [Si], [Al] (mol L-1). The interpolating equation of density as a function of sodium bicarbonate concentration [Na+] used to estimate the influence of chemical impurities on the density measurements was:
(1) dNaHCO3 = 0.99704+0.0638×[Na+]×10-5 R2 = 0.93
Figure 4 shows sample density [(d-d0)×105 (g cm-3)] as a function of specific conductivity (μS cm-1), and the good linear correlation between the two parameters (Y= 0.0794 ± 0.0020, R2 = 0.9649). In this case the error bar is estimated as 2% of (d-d0)×105. Clearly, the experimental uncertainty cannot be responsible for the observed data.
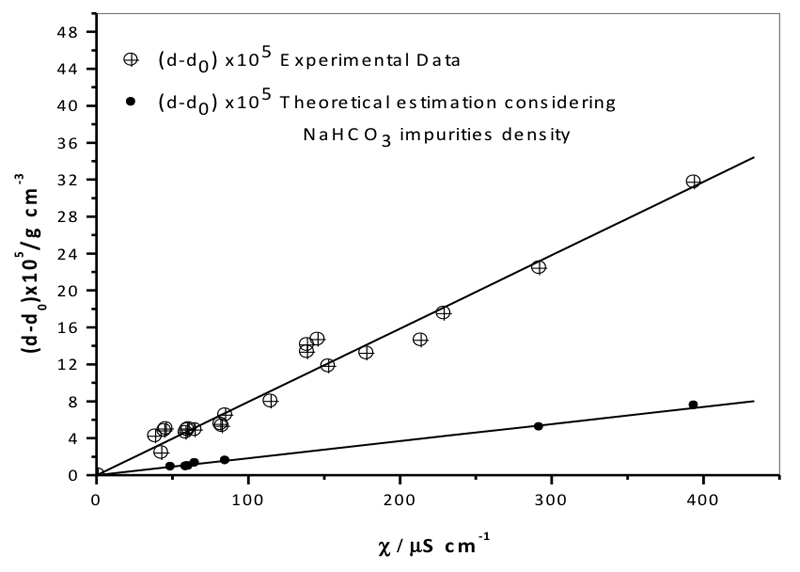
Figure 4: Density vs. specific electrical conductivity as measured experimentally (see Table 4) correcting for the effect of sodium bicarbonate impurities on density (NaHCO3 impurity density was calculated using Eq. 1). The error bars of the largest standard deviation for conductivity and density are too small to be seen.
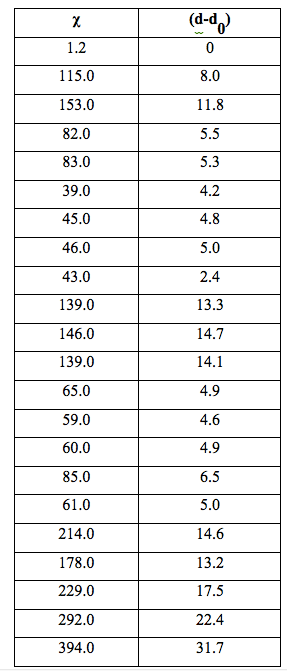
Table 4: Specific electrical conductivity χ (µS cm-1) and difference between density (d) of filtered samples and density (d0) of water (g cm-3×105).
![Table 5: Specific electrical conductivity, χ (µS cm-1), number of filtrations, N, density, d (g cm-1) of water samples filtered with R4 filter (pore size 5-15 µm), concentrations of sodium bicarbonate [Na+], boric acid [B], silicic acid [Si] and aluminium oxide [Al] (mol L-1×105) impurities released from the glass containers.](/uploads/vol7/elia/Table-5.png "Table 5: Specific electrical conductivity, χ (µS cm-1), number of filtrations, N, density, d (g cm-1) of water samples filtered with R4 filter (pore size 5-15 µm), concentrations of sodium bicarbonate [Na+], boric acid [B], silicic acid [Si] and aluminium oxide [Al] (mol L-1×105) impurities released from the glass containers.")
Table 5: Specific electrical conductivity, χ (µS cm-1), number of filtrations, N, density, d (g cm-1) of water samples filtered with R4 filter (pore size 5-15 µm), concentrations of sodium bicarbonate [Na+], boric acid [B], silicic acid [Si] and aluminium oxide [Al] (mol L-1×105) impurities released from the glass containers.
Figure 4 also shows the trend of (d-d0)×105 vs. χ for (d-d0), correcting for the density of NaHCO3 estimated using Equation 1 with the experimental values for the sodium concentration. The contribution of sodium bicarbonate impurities to sample density was clearly small. The density of filtered water samples was much higher than that of unfiltered water, despite the fact that the impurities contributed to the value (see Table 9). The higher the electrical conductivity, the higher the density. This means that the increase in density is caused by the same phenomenon that causes the increase in conductivity.
The quantitative determination of impurities showed that the contribution from sodium bicarbonate, the most abundant impurity, increased with the number of filtrations but remained below 10-30% of the parameters measured. Chemical contribution to the parameters cannot explain their sharp increase. Experimental uncertainty cannot be responsible for the observed data because of the relatively small values of standard deviation, 2-5% of the measured density and conductivity. Conductivity increased more than two orders of magnitude while σ was 0.025% of the whole increase. Density increase was about 35×10-5 g cm-3, while the standard deviation was 0.2×10-5 g cm-3, that is, 0.57% of the whole increase.
A working hypothesis could be to consider water filtration akin to water passing through fine capillaries. The iterative procedure is thus connected with a flow of energy and matter in an open system. The energy flux is partially dissipated as heat, enabling the formation of “dissipative structures” (Prigogine, 1977; Nicolis, 1989). This perturbation appears to trigger the formation of molecular aggregates of water (water clusters, aqueous nanostructures, molecular aggregates of water) that increase the effects of the proton hopping mechanism (De Grotthuss, 1806; Gileadi et al., 2006) Such structures lead to an increase in χ (μS cm-1) and density by virtue of a denser bundling of water molecules. As already mentioned, exclusion zones presumably play a not secondary role in determining the formation of aggregates of water molecules. (Zheng et al., 2006).
Conclusions
The experimental data showed a significant variation in some physico-chemical parameters of Milli-Q water after iterative filtration. Conductivity was 1-2 orders of magnitude higher than initial values after iterative filtration. The increase in the conductivity and density of water was permanent and often increased with time. The systems studied are non-equilibrium systems in which irreversible processes occur. This new field of research on water opens up a completely new scenario whereby the supramolecular structure of liquid water can be modified by mechanical perturbations or ageing, especially ageing in small volumes. This characteristic may be linked to the very different properties of water contained in biological cells. We are not yet able to discuss the nature of the dissipated energy or the kind of water structures formed. The unique volume effect that characterizes the behaviour of these samples is a major feature of dissipative structures. The peculiarities of iteratively filtered water are in line with the hypothesis of aqueous nanostructures in liquid phase.
References
Bakker HJ, Kropman MF, Omta AW (2005). Effect of ions on the structure and dynamics of liquid water. J Phys: Condensed Matter 17: 3215-3224.
Ball P (2008). Water: water-an enduring mystery. Nature 452(7185): 291-2.
Capolupo A, Del Giudice E, Elia V, Germano R, Napoli E, Niccoli M, Tedeschi A, Vitiello G. (2014). Self –similarity properties of nafionized and filtered water and deformed coherent states. Int J Mod Phys B 28: 1450007.
Chiriach S, Lozneanu E, Sanduloviciu M (2006). Self –organisation as physical basis of the hysteresis phenomena. J Optoelec Adv Mat 8(1): 132 – 134.
De Grotthuss CJT (1806). Ann Chim 58: 54-74.
Elia V, Niccoli M (1999). Thermodynamics of extremely dilute aqueous solutions. Ann NY Acad Sci 879: 241-248.
Elia V, Niccoli M (2000). New physico-chemical properties of water induced by mechanical treatments. J Therm Anal Calor 61: 527-537.
Elia V, Niccoli M (2004). New physico-chemical properties of extremely diluted solutions. J Therm Anal Calor 75: 815-836.
Elia V, Elia L, Napoli E, Niccoli M (2006). Conductometric and calorimetric studies of serially diluted and agitated solutions: the dependence of intensive parameters on volume. Int J Ecodynamics 1: 1-12.
Elia V, Napoli E (2010). Dissipative structures in extremely diluted solutions of homeopathic medicines. A molecular model based on physico-chemical and gravimetric evidences. Int J Design and Nature 5(1): 39-48.
Elia V, Napoli E, Niccoli M (2010). Thermodynamic parameters for the binding process of the OH- ion with the dissipative structures. Calorimetric and conductometric titrations. JTAC 102(3): 1111-1118.
Elia V, Napoli E (2012). Nanostructures of water molecules in iteratively filtered water. KEM 495: 37- 40.
Elia V, Marchettini N, Napoli E, Niccoli M (2013a). Calorimetric, conductometric and density measurement of iteratively filtered water using 450, 200, 100 and 25 nm Millipore filters. JTAC 114(2): 927-936.
Elia V, Napoli E, Niccoli M (2013b). Calorimetric and conductometric titrations of nanostructures of water molecules in iteratively filtered water. JTAC 111: 815-821.
Elia V, Ausanio G, De Ninno A, Gentile F, Germano R, Napoli E, Niccoli M (2013c). Experimental Evidences of Stable Aggregates of Water at Room Temperature and Normal Pressure after Iterative Contact with Nafion Polymer Membrane. WATER Journal 5: 16-26.
Elia V, Ausanio G, Gentile F, Germano R, Napoli E, Niccoli M (2014a). Experimental evidence of stable water nanostructures in extremely dilute solutions, at standard pressure and temperature. Homeopathy 103: 44-50.
Elia V, Ausanio G, De Ninno A, Germano R, Napoli E, Niccoli M, (2014b). Experimental Evidences of Stable Water Nanostructures at Standard Pressure and Temperature Obtained by Iterative Filtration. WATER Journal 5: 121-130.
Errington JR, Debenedetti PG (2001). Relationship between structural order and the anomalies of liquid water. Nature 409: 318-321.
Gileadi E, Kirowa-Eisner E (2006). Electrolytic conductivity – the hopping mechanism of the proton and beyond. Electrochimica Acta 51: 6003-6011.
Gregory JK, Clary DC, Liu K, Brown MG, Saykally RJ (1997). The water dipole moment in water clusters. Science 275: 814-817.
Kropman MF, Bakker HJ (2001). Dynamics of Water molecules in aqueous solvation shells. Science 291: 2118-2120.
Lo SY (1996). Anomalous state of ice. Mod Phys Lett B 10: 909-919.
Lo SY, Lo A, Ching LW, Tianzhang L, Hua LH, Geng X (1996). Physical properties of water with IE structure. Mod Phys Lett B 10: 921-930.
Lo SY, Xu G, Gann D (2009). Evidence for the existence of stable-water-clusters at room temperature and normal pressure. Phys Lett A 373: 3872-3876.
Lobyshev VI, Shikhlinskaya RE, Ryzhikov BD (1999). Experimental evidence for intrinsic luminescence of water. J Mol Liq 82: 73-81.
Lobyshev VI, Solovey AB, Bulienkov NA (2003). Computer construction of modular structures of water. J Mol Liq 106: 277-297.
Malescio G, Franzese G, Skibinsky A, Buldyrev V, Sergey V, Stanley HE (2005). Liquid-liquid phase transition for an attractive isotropic potential with wide repulsive range. Phys Rev E 71: 061504/1-061504/8.
Mishima O, Stanley HE (1998). Decompression-induced melting of ice IV and the liquid–liquid transition in water. Nature 392: 164-168.
Montagnier L, Aissa J, Ferris S, Montagnier J, Lavallée C (2009). Electromagnetic signals are produced by aqueous nanostructures derived from bacterial DNA sequences. Interd Sci Comput Life Sci 1: 81-90.
Marchettini N, Del Giudice E, Voeikov V, Tiezzi E (2010). Water: A medium where dissipative structures are produced by coherent dynamics. Journal of Theoretical Biology 265: 511-516.
Nicolis G (1989). Physics of far –equilibrium systems and self-organization. In: The New Physics. Ed Davies P, Cambridge University Press, New York.
Popescu M (2003). Self organisation in non crystalline solid. J Optoelec Adv Mat 5(5): 1059 – 1068.
Prigogine I (1977). Time, structure and fluctuations. Nobel Lecture, 8 Dec, 1977.
Rey L (2003). Thermoluminescence of ultra-high dilutions of lithium chloride and sodium chloride. Physica A 323: 67-74.
Robinson GW, Cho CH, Gellene GI (2000). Refractive index mysteries of water. J Phys Chem B 104: 7179-7182.
Ropp J, Lawrence C, Farrar TC, Skinner JL (2001). Rotational motion in liquid water is anisotropic: a nuclear magnetic resonance and molecular dynamics simulation study. J Am Chem Soc 123: 8047-8052.
Samal S, Geckeler KE (2001). Unexpected solute aggregation in water on dilution. Chem Commun 21: 2224-2225.
Sanduloviciu M, Dimitriu DG, Ivan LM, Aflori M, Furtuna C, Popescu S, Lozneanu E (2005). Self-organization scenario relevant for nanoscale science. J Optoelec Adv Mat 7(2): 845 – 851.
Wourtersen S, Emmerichs U, Bakker HJ (1997). Femtosecond Mid-IR pump-probe spectroscopy of liquid water: evidence for a two-component structure. Science 278: 658-660.
Woutersen S, Bakker HJ (1999). Resonant intermolecular transfer of vibrational energy in liquid water. Nature 402: 507-509.
Yinnon TA, Elia V (2013). Dynamics in perturbed very dilute aqueous solutions: theory and experimental evidence. Int J Mod Phys B 27(5): 1350005-1350040.
Zheng, J.M.; Chin, W.C.; Khijniak, E.; Khijniak, E. Jr.; Pollack, G.H (2006). Surfaces and interfacial water: evidence that hydrophilic surfaces have long-range impact. Adv Colloid Interface Sci 127: 19-27.
Discussion with Reviewers
Reviewer 1: I have doubts whether the behavior observed can be ascribed to water nanostructures formed upon a filtration process or explained by another mechanism – from the clarity point it is on the border line.
Elia V, Marchettini N, and Napoli E: We agree that in the current state of research on the mechanism of formation of nanostructures, there are no still certainties. Anyway the presence of nanostructures in solution has been highlighted with certainty. [See Elia et al., 2013b and Elia et al., 2014b] However, we are open to new hypotheses.