The Ascent of Sap in Tall Trees: a Possible Role for Electrical Forces

The Ascent of Sap in Tall Trees: a Possible Role for Electrical Forces

Johnson B1*

1Independent Researcher, Oxford, UK

*Correspondence E-mail: bob.johnson1000@gmail.com

Key Words: Ascent of Sap, Multi-force Theory, Electrical Forces

Received May 6th, 2013; Accepted October 19th, 2013; Published November 3rd, 2013; Available online November 10th, 2013

doi: 10.14294/WATER.2013.9

 

Abstract

The debate continues between proponents of the widely-accepted Cohesion-Tension Theory and those who consider that other forces, represented by the chemical potential equation, may also be involved in the ascent of sap. It has long been known that electrical potential differences exist in living trees but no viable mechanism has yet been proposed whereby these potential differences may help drive the flow in the xylem. More recently, it has been discovered that various mechanisms exist which can create large zones of charge separation in water. Combining these results here leads to a possible mechanism whereby the known electrical potential differences in trees could assist in driving sap flow. It is concluded that the electrical potential term in the water potential equation should be considered when investigating the range of possible forces involved in the ascent of sap. The role of the natural vertical electric field of the Earth is discussed in relation to generation of the observed potentials in living trees and various corollaries of the inclusion of electrical forces are suggested.

“The Cohesion – Tension Theory has prevailed largely unmodified for over 100 years, a somewhat unusual situation for a scientific paradigm explaining a fundamental process.” (Meinzer, Clearwater & Goldstein 2001, p243)

 

Article Outline

 

Introduction

Proponents of the widely-accepted Cohesion-Tension Theory (CTT), originally postulated separately by Dixon & Joly and Askenasy at the end of the nineteenth century, argue that CTT provides the only driving force needed to drive the ascent of sap in trees. Other researchers suggest that alternative forces may be involved, and indeed may be necessary to explain both why cavitation in the xylem is not fatal to the flow and the various anomalous experimental results indicating that the predicted negative pressure gradients are often not found in living trees (e.g. Balling & Zimmermann 1990, Zimmermann U, Wagner & Schneider 2000; Zimmermann U. et al. 1994, 2002 a,b, 2004; Zimmer-mann D. et al. 2007; Westhoff et al. 2007).

The arguments in favor of CTT are too well-known to need repeating here. Even those who argue for additional forces accept that pure water can sustain the tension necessary to support sap ascent in tall trees when the xylem is uncavitated. (e.g. Zimmermann U. et al. 2002a)

However it is worth remembering that Dixon & Joly themselves pointed out that: “…. the view formerly widely accepted, that the lumina of the conducting tissues during the time of active transpiration for the most part contain gas, if correct, would render our explanation untenable.” – (Dixon & Joly 1895, p571)

Even proponents of CTT acknowledge the presence of embolisms in the xylem (e.g. Tyree 1997, Holbrook & Zwieniecki 1999).

If CTT is the only mechanism involved then the high tensions required for sap ascent in tall trees implies that the sap must be in a metastable state. The equilibrium vapour pressure of water is only +2 kPa at room temperature (Zimmermann U. et al. 2004), well below the magnitude of the necessary tensions, implying that any slight disturbance, imperfection or pressure reduction due to constriction in the column of suspended sap would be expected to lead to immediate cavitation as air comes out of solution (Canny et al. 2007).

These considerations suggest that there may be additional mechanisms involved in the ascent of sap in tall trees, as Meinzer et al. (2001, p245) concluded. Zimmermann U. et al. (2004) suggest an alternative based on the Plumb & Bridgman (1972) model, arguing that a chemical potential gradient could, in theory, balance the hydraulic pressure gradient.

Zimmermann U. et al. (2004) considered a number of alternative factors whereby a chemical gradient could be generated and thereby developed the theory of multi-force lifting. They also considered the possibility of electrical forces being involved, but without suggesting a mechanism whereby electrical forces could play a role.

They concluded that: “…electrical effects on water lifting cannot be ignored a priori, even if they only trigger other processes that ultimately lead, via coupling, to bulk water flow.” -(ibid., p603)

This paper will consider a possible mechanism whereby electrical effects could come into play in the ascent of sap in tall trees.

 

Previous Electrical Measurements On Living Trees

In 1963, Fensom observed that: “Electrical measurements on living trees have been conducted from time to time, although they are still not commonly used by plant physiologists.” (Fensom 1963, p831)

Despite a recent resurgence in interest in bioelectricity in plants, (e.g. Volkov 2012), electrical measurements on living trees are still relatively rare. However, there are a number of relevant studies reported in the literature, many of which investigated a possible relation between the vertical potential difference and the sap flow based on generation of the potential by electro-osmotic streaming.

In the 1920s & 1930s, Lund investigated bio-electric currents in various plants in relation to their metabolism and cell respiration. (Lund 1925, 1928a,b, 1929a,b, 1930a, 1931 a,b,c, 1931a,b; Lund & Kenyon 1927; Lund & Bush 1930b). In one experiment on a living Douglas Fir tree (Pinaceae Pseudotsuga menziesii), Lund measured a vertical potential difference of ~50mV/m with the apex positive with respect to the base and ground. (Lund 1929a, Figs 3 & 6), a result he explained in terms of a Theory of Continuous Bio-electric Currents.

Further investigations in the same series confirmed this result. As Rosene later summarized when reporting on Lund’s findings:  “Apical regions in the stem are electro-positive in the external circuit to relatively more basal regions. Similarly, the apex of each branch has a higher potential than basal regions of that branch.” (Rosene 1937, p391)

In the 1940s, Burr (1945, 1947) investigated the electrical potentials in living maple trees and found that, although the potentials were variable, the upper part of the tree was positive with respect to the base from late May through to the end of December. (Burr 1947, Fig 2 p313)  “During the spring and summer, the upper electrode became steadily more positive and before the leaves fell in the fall the potential had already started to rise markedly.” (ibid. p314)

Fensom carried out a series of investigations into the bio-electric potentials of plants in the 1950s & 1960s (Fensom 1957, 1958, 1959, 1962, 1963a] which included continuous measurements of bioelectric stem potentials in three kinds of tree (Ulmus americana L., Pinus resinosa Ait., and Acer saccharum Marsh). Fensom demonstrated a yearly tendency for the upper electrode in the Elm trees to become more positive with respect to ground, and a daily cycle with a definite daily rhythm (Fensom 1963a, p833). The other trees were similar.

Further investigation showed that:  “It is now clear that the measurements recorded in this study have all been measurements in the xylem.” (ibid. p847)

Fensom’s results showed that the upper electrode was generally, but not always, positive with respect to the base. He concluded: “These facts support the hypothesis that in old wood the potential differences are to a large measure streaming potentials [from electro-osmotic flow], and reflect the rates of movement of water up the tree. But in young wood close to the cambium this correlation no longer holds consistently and other hypothesis must be introduced.” (ibid. p848)

Fraser-Smith (1978) investigated the Ultra Low Frequency (ULF) [i.e. less than 5 Hz] components of the potentials in the stem of a large Native Oak, Quercus lobata. He found a potential difference (pd) of between 10 – 100 mV between two electrodes 0.76 m apart. The upper electrode was positive.

Studies by Schuch (1968) and Morat, Le Mouël & Granier (1994), quoted in Gibert et al. (2006), also found electrical potential gradients in a spruce tree and a chestnut tree respectively.

Gindl, Löppert & Wimmer (1999) found “… a strong linear relationship … between the velocity of a defined liquid streaming through a stem of Salix alba L. and the electrochemical potential (streaming potential).. ”

However, as Gibert et al. (2006) pointed out, “The positive sign of the streaming potential coefficient obtained in the lab-oratory … does not agree with the sign of the observed electric daily variation in the tree trunk.” (ibid. p573)

Gibert et al.’s own study on a poplar tree (Populus nigra L) found electric potentials in the tree which had some relation to the sap flow, but concluded that “These observations cannot be reconciled with the electrokinetic mechanism in its simple form.” (Gibert et al. 2006, p581)

Koppán et al. (2000, 2002) found an upper-positive potential gradient of ~50 mV/m, similar to Lund’s figure, beneath the cambium in Turkey Oak (Quercus cerris L.) (Koppán et al. 2000, Fig 2). They later concluded: “We found a remarkable correlation between electric potential differences (EPD), the water potential of air and sap flux density data. It means that the EPD follows the variations of the sap flow intensity.” (Koppán et al. 2002, p37)

Interestingly Koppán et al.’s results show an inverse correlation between the potential difference and the upward sap flow. An increase in sap flow correlates to a small decrease in the potential gradient. Although the authors conclude that “sap streaming due to the transpiration and root pressure generates the largest part of measured potential differences” (ibid. p38), their results actually seem to lend further support to Fensom’s conclusion that electro-osmotic streaming could not explain his results in young wood.

In summary, there is now a considerable body of evidence that variable electrical potentials do exist in living trees but attempts to correlate these potentials with tension-driven sap flow via an electro-osmotic streaming mechanism have not met with success. As Gibert et al. (2006) concluded in relation to Koppán’s study: “While the observed daily variation could be reasonably interpreted at first in terms of streaming potentials, the relationship between the sap flow and the electric potential variation therefore remains puzzling.” (Gibert et al. 2006, p573)

In summary, there appears to be a correlation between observed electric potentials and sap flow, but the potentials do not seem to arise from electro-osmotic flow. The evidence seems to suggest instead that the potentials may be involved in driving the flow by another mechanism.

 

Towards an Alternative Electrical Mechanism

The effect of a potential gradient on ions in the xylem sap

A voltage gradient is defined as equivalent to an electric field strength; the force on an ion in an electric field is defined as the product of the electric field strength and the charge on the ion.

Any ions in the tree will therefore experience an electrical force due to the internal potential gradient or electric field. The electric force in any one member (e.g. stem or branch) will depend on the longitudinal potential gradient along that member, which may vary around different parts of the circumference. Radial potential gradients may also occur but are not significant to the present discussion except in so far as they might modify the longitudinal potential gradient in the xylem.

Assuming that the apices are positive relative to the base, as found by most researchers, then positive ions will be attracted towards the Earth while negative ions will be repelled from the ground, i.e. upwards in the tree and out along the branches.

Xylem sap generally is known to contain a variety of both positive and negative ions. (e.g. Gollan Schurr & Schulze 1992). The sap was presumed to be charge-neutral, although in cases of high ion concentration the total measured negative anions exceeded the total measured positive cations; the difference was assumed to be made up by a ‘group of cationic substances which were not analyzed’ (ibid. p553).

Proceeding on the assumption that xylem sap is indeed charge-neutral overall, the obvious question is how this could result in a net electrical force on the sap; any upward force on the negative ions would apparently be balanced by an equal downward force on the equal number of positive ions in the sap.

But this assumes that the positive and negative ions are uniformly distributed throughout the xylem sap and equally free to move upwards or downwards under the influence of the electrical forces. There is a growing body of evidence that this may not be the case and that the positive and negative ions may in fact be partially separated into different radial zones within the xylem lumen.

If this result is valid, adhesion to the vessel walls should be expected to affect ions of one charge more than ions of the opposite charge. In effect, one set of charges would be more restrained than the other, leading to more mobility in one direction than the other under the influence of the electrical force.

Evidence of charge separation within the xylem

a. Charge separation due to bound charge on the xylem walls
It is known that the xylem walls carry a bound negative surface charge integral to the wall structure: “The cell walls in general show a high cation-binding capacity, with pK in the neighborhood of 2.8. One is, therefore, assured that even in the slightly acidic xylem sap, the wall phase will have negative fixed charges.” (Amin 1982, p106)

The bound negative charge attracts a layer of positive charge in the sap. The effect is to form an electrical double layer adjacent to the walls: “Xylem walls generally have a net negative bound surface charge neutralized by an excess of mobile cations in the sap close to the charged surface. The presence of negatively charged, gel-like compounds attached to the wall will also enforce the formation of an electrical double layer at the inner walls of the conducting xylem elements.” (Zimmermann U. et al. 2004, p603)

Note that the double layer will form whether or not the gel-like compounds are present.

The mobility of the positively-charged cations close to the charged wall surface might be expected to be reduced due to the adhesion to the negatively-charged walls. This effect is known to exist in electro-osmotic flow and, although electro-osmotic flow is not under consideration here, the adhesion of the positive cations to the walls may still be relevant.

b. Charge separation and support by binding to mucilage
Zimmermann U. et al. (2002b, 2004) have identified layers of mucilage adjacent to the xylem walls. This mucilage may be a consequence of damage to the xylem, as some physiologists maintain (e.g. Crews, McCully & Canny, 2003). Alternatively, if it is present in undamaged xylem vessels, then positive ions may be expected to adhere to the negatively-charged mucilage. In which case, the electrical force from the internal electric field acting on the positive ions will be transmitted via the mucilage to the xylem walls and thence to the structure of the tree.

The mucilage would then act to provide support preferentially to the positive ions in addition to or as an alternative to the adhesion forces suggested above.

c. Charge separation due to hydrophobicity of xylem walls
Some researchers have found that the xylem walls are partially lined with a lipid layer which, in combination with the lignin in the walls, renders them hydrophobic. (e.g. Zimmermann U. et al. 2002a)

This may be an over-simplification. The hydrophobic lining to the xylem walls is interrupted at frequent intervals by pores with hydrophilic linings. In Canny’s words: “The inner walls of vessels are a mixture of hydrophilic and hydrophobic surfaces, and the latter predominates in large mature vessels. …. Thus to the flowing stream in the vessels, the walls are predominantly hydrophobic, but they are also easily wetted by water because of the strongly hydrophilic nature of the frequent pits.” (Canny, private communication)

In different contexts, Pollack and co-workers (e.g. Zheng & Pollack 2006, Klyuzhin et al. 2008) have demonstrated that hydrophilic surfaces form negatively-charged EZ layers in water adjacent to the surface. Positive ions are excluded from the EZ layer, which can be up to 400μm thick in experimental situations. (Zheng & Pollack 2006). This research shows that charge separation can be maintained between adjacent layers of a liquid, and also that the charge-separated layers can form an annulus and core arrangement in a tube.

It seems possible that hydrophobic surfaces may act in the opposite manner as the counterpart of the behavior of hydrophilic surfaces. If this is the case then the predominantly hydrophobic nature of the xylem walls could itself cause the required charge separation. In contrast to the nanometre-scale double layers associated with electro-osmosis, a positive EZ layer adjacent to the xylem walls could easily be of a scale sufficient to separate the xylem sap in vessels of up to 500μm diameter (Sperry 2003) into an positive annulus and negative core of similar areas.

Effect of charge separation by one or more of the above mechanisms

Recalling that sap is assumed to be overall charge-neutral, and further assuming that an annulus of positive cations forms adjacent to the xylem walls by one or more of the mechanisms discussed above, then in order to maintain the overall neutrality of sap at any cross-section in the xylem, an equal number of negative ions must be concentrated into the centre of the lumen.

In contrast to the positive ions which may be subject to adhesion forces with the vessel walls, the negative ions in the core region will retain their mobility in the sap.

Negative charges will tend to attract adjacent polarized water molecules with which they form hydrogen bonds. Cohesion between water molecules, as well-established in CTT, will ensure that each negative charge will effectively be bound to a large number of neutral water molecules.

The effect is similar to viscous drag as observed in electro-osmotic flow. For example, Fensom & Dainty (1963b) found that the viscous drag effect in xylem sap subjected to an applied electric field was of the order of 100 moles per Faraday. In other words, each charged particle dragged 100 neutral molecules with it when subject to high applied electro-osmotic potentials. This caused rapid bulk flow in the sap.

In the much smaller potentials under consideration here, it seems likely that this figure should be considered to be a minimum because the potential gradient, and therefore the driving force on each ion, is less. This results in a smaller ion velocity which therefore requires a smaller viscous drag between the ion and the water molecules in order to carry the water molecules with the ion. Therefore a longer chain of polarized water molecules could be attached to each slowly-moving negative ion before the hydrogen bond strength was exceeded.

The effect on the negative core sap is similar to a mechanical bucket wheel; each volume of water is supported independently of the others because the electrical force acts directly on each ion in the sap. It is not necessary to have a continuous column of water which generates a differential hydraulic pressure across each cross-sectional ‘slice’ of sap in the xylem; nor is it necessary to have semi-permeable membranes providing physical support to each separate element.

In summary, we suggest that the electrical term in the chemical potential equation (see for example Nobel 2005, pp 59-61) may become effective due to an EZ-layer-like radial charge separation over the whole xylem cross-section, combined with adhesion forces acting on positive ions in the annulus near the xylem walls but not on the negative ions in the core.

It should be noted that the postulated electrical effect does not necessarily equate to the driving force causing sap to ascend. As in the case of the Plumb and Bridgman model, the principal effect is to reduce the hydraulic gradient by countering the gravitational force and thereby allow small tensions, hydraulic pressures or concentration gradients to drive the flow upwards.

This could explain why the measured electrical effects are too small to drive electro-osmotic flow, as Fensom found (1963a). The electrical forces are only one component in the total equation.

Quantification of the proposed effect

A limited amount of experimental evidence already exists whereby the proposed effect may be quantified approximately.

Using Lund’s measurement of 50 mV/m potential gradient in living Douglas Fir trees (Lund 1929a, Figs 3 & 6), the weight of the sap in the core could be supported if there was a net negative charge equivalent to 2.08 mol/m3 of singly-ionized molecules in the core sap and if hydrogen bonding and cohesion together were sufficient to transfer the force to the surrounding water molecules by the viscous drag mechanism as discussed above.

According to Gollan et al. (1992), the principal negative ion in xylem sap is nitrate, NO3–. The nitrate content in sunflower, Helianthus annuus, is of the order of 7.33 mol/m3 (ibid. Table 1). If this can be taken as a typical value for trees then only 28% of the balancing positive ions would need to be attracted into the positive annulus for the negative core sap to be fully supported by the electrical force.

Amin (1982) has demonstrated that the energy stored in the electrical double layer formed by the xylem walls is sufficient to balance the potential energy in the raised xylem sap. These figures suggest that the postulated mechanism is feasible in principle.

 

The Earth’s Vertical Electric Field

Background

One factor that has seldom been considered recently is the well-known vertical atmospheric electric field. As Le Mouël, Gibert & Poirier (2010) pointed out: “Studies of the electric potential and atmospheric conductivity at the ground surface were vigorous, up to the Second World War …. In the middle of the XXth century, the interest waned, but a renewal of interest might well be on its way.” (ibid. p98)

The vertical electric field arises between the negative charge on the surface of the Earth itself and the more positive ionosphere. (e.g. Chalmers 1950)

Because a tree is known to be able to conduct electricity, it may be relevant to the discussion of electric potentials in the tree to consider the behavior of a conductor in the Earth’s electric field. It appears possible that the vertical atmospheric electric field may contribute to the observed potentials in trees. This section will explore that possibility with reference to Figures 1 & 2 and suggest a mechanism whereby it could be realized.

Details of the Earth’s Field
The vertical electric field at the surface of the Earth varies geographically, seasonally and diurnally within a range of ~200 V/m to ~550 V/m with a mean value of 365 V/m (Chalmers 1950)

The surface of the Earth carries a mean net negative surface charge density of 9.6 x 10-4 ESU/cm2 (-3.2 x 10-13 C/cm2). Relative to the Earth, the ionosphere is at a positive potential of +40,000 V (ibid.). Although the surface of the Earth is negatively charged, it is usually taken as the zero reference potential i.e. any object electrically connected to the Earth is assumed to be ‘grounded’ and have no potential. Whilst useful for many everyday measurements, this concept is somewhat misleading, analogous to taking zero degrees Celsius as a measure of temperature. An earthed object has a negative potential in the same way that a body at zero degrees Celsius has an absolute temperature.

Air is not a perfect insulator due to the small amount of natural ionization present in the atmosphere. Therefore the vertical electric field results in a fine weather air-Earth current with a mean current density of 1.12 x 10-16 A/cm2 measured at Kew, London, and 3.2 x 10-16 A/cm2 over the oceans. (ibid. Appendix, p164)

The behavior of a conductor in the Earth’s field

If the air was a perfect insulator then any vertical conductor with its base in contact with the charged Earth would acquire sufficient negative charge to reach the same electric potential as the Earth. The negative charge would not be able to leak away into the surrounding air. There would be no potential gradient in the conductor because it would all be at the same potential as the Earth’s surface.

However, the fact that air is not a perfect insulator means that some negative charge will leak from the conductor into the air, to be replaced with more charge from the Earth. At the same time, positive ions will arrive at the conductor and be transmitted to Earth. In effect, a conductor with its base in contact with the Earth will form part of an electrical circuit between the Earth’s surface and the ionosphere. The leaking charge amounts to an electric current from the air, through the conductor to the Earth.

Every conductor (except a superconductor) has an electrical resistance. Therefore when a current passes through the conductor there will be a potential drop along it proportional both to the current that is passing and to the resistance of the conductor itself.

This is exactly analogous to water passing through a pipe. The pressure is equivalent to the potential. If there is no flow (current) then the pressure is the same all along the pipe. When a tap is opened at one end and flow starts, hydraulic friction (resistance) causes a pressure drop (potential drop) along the pipe.

It is important to note that the conductor is not subject to the same potential gradient as the air alongside the conductor. The potential gradient along any electrical path depends on the resistance of the path and the current along the path. Therefore different paths, such as the one through the conductor and the one through the air near it, will exhibit different potential gradients because of their different resistances and currents.

The small resistance of the conductor relative to the air alongside it will result in a small potential gradient in the conductor relative to the potential gradient in the highly resistive air alongside.

A tree as an element in the air – Earth electric circuit

Trees are known to be relatively good conductors of electricity. (e.g. Lund 1929a,b; Fensom 1957-1963; Le Mouël et al. 2010) Therefore part of the normal fine weather current Iair will pass through the tree; the current along this path is Itree.

As indicated in Figure 1, a tree is a low-resistance element in series with a very high resistance element representing the partially-ionized air between the top of the tree and the ionosphere. The driving potential is the potential difference of 40,000 V between the ionosphere and Earth. The total current through the ionosphere –tree – Earth path will be determined mainly by the high resistance of the column of air above the tree and will therefore be very small despite the relatively low resistance of the tree itself.

 

Figure 1: Air-Earth current paths and the Potential of the Atmosphere. The +40,000 V potential of the ionosphere compared to Ground (= Reference Zero* for Voltage measurements) causes a fine-weather air-Earth current I (air), part of which will pass through a tree, I(tree). The electrical resistance of the tree R(tree) will cause a small voltage drop dV(tree) over the height of the tree (see Fig. 2). The right hand figure shows diagrammatically that both the potential and the potential gradient of the atmosphere vary with height; near ground level, the potential gradient is ~365 Volts/metre. Values are taken from Chalmers (1950). V = Voltage; I = Current; R = Resistance; -ve = negative. * Note that the Earth’s surface is negatively charged; taking the Ground as reference zero for potential measurements is merely an arbitrary convention similar to taking the freezing point of water as the reference zero for temperature measurements in the Celsius scale.
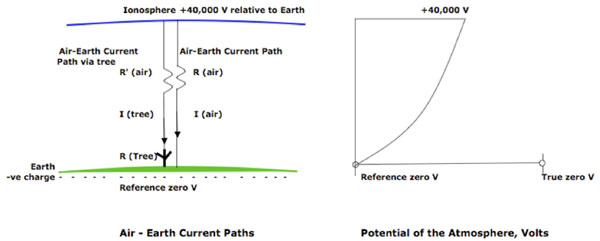
Figure 1: Air-Earth current paths and the Potential of the Atmosphere. The +40,000 V potential of the ionosphere compared to Ground (= Reference Zero* for Voltage measurements) causes a fine-weather air-Earth current I (air), part of which will pass through a tree, I(tree). The electrical resistance of the tree R(tree) will cause a small voltage drop dV(tree) over the height of the tree (see Fig. 2). The right hand figure shows diagrammatically that both the potential and the potential gradient of the atmosphere vary with height; near ground level, the potential gradient is ~365 Volts/meter. Values are taken from Chalmers (1950).

 

V = Voltage; I = Current; R = Resistance; -ve = negative.* Note that the Earth’s surface is negatively charged; taking the Ground as reference zero for potential measurements is merely an arbitrary convention similar to taking the freezing point of water as the reference zero for temperature measurements in the Celsius scale.

The current through the tree will cause a potential drop along the height of the tree. The magnitude of the potential drop will be a function of the resistance of the tree and the total current passing through it.

Recalling that the tree would be at the same negative potential as the Earth if there was no current, the potential drop (dV Tree) from apex to base would result in a less negative potential at the apex. If the Earth is taken as the zero reference potential, or ‘ground’, as is often assumed to be the case, the apex will appear positive with respect to the base.

This is apparently the result found by Lund (e.g. 1929a) and others (see above) who showed that apices are typically positive with respect to the bases and ground.

The current in each part of the tree will depend on the resistance of the total path through that path. As Le Mouël et al. (2010) stated, the electric current in the stem will be divided at forks between the trunk and the limbs, as indicated in Figure 2.

If the resistance in the air-tree-Earth current path through the tree is reduced then the current will increase. Part of the resistance in the current path arises at the surface of the leaves where the charge carriers have to pass from the air to the leaf or vice-versa.

It is important to realize that the rate of transfer of charge carried across the surface boundary depends on the potential gradient immediately adjacent to the surface. Because air is a poor conductor, any potential difference between the surface and the air will be concentrated into a very thin layer of air next to the surface. Therefore, a small potential difference can result in a very high local potential gradient which is sufficient to enable charge transfer across the boundary.

A number of factors can influence the ease with which charge carriers can cross this boundary, and therefore the overall resistance to air-Earth current flow through the tree.

As shown in Figure 2, the potential gradient in the tree is very small compared to the atmospheric potential gradient alongside the tree. Therefore, the higher the tree grows, the greater the potential difference between the top of the tree and the air becomes. As the tree grows taller, the local electric field in the air in contact with the leaf surfaces becomes stronger and more current can leak from leaves to air. This in turn increases the potential gradient in the tree and increases the lifting force on the sap. In effect, the tree would be using the energy of the Earth’s electric field to assist lifting the sap to greater heights.

 

Figure 2: Currents and Potentials in tree and air paths. Some current will pass along the apex (Ia) and all the branches (Ib) to the main trunk of the tree. The currents through the tree I(tree) cause a potential gradient ( = Electric Field Intensity) dV(tree) in the tree but this is small compared to the normal atmospheric potential gradient of ~365 V/m in the air adjacent to the tree. Therefore as the tree grows higher, the potential difference dV(air) between the top of the tree and the air at that height increases significantly, enabling the tree to pass more current and hence generate a stronger internal potential gradient. V = Voltage; I = Current; E = Electric Field Intensity (=potential gradient) in Volts / metre; dV(tree) = Voltage drop over height of tree*; dV (air) = the potential difference between the top of the tree and the air at that height. * potential measurements in 2.4m tall Douglas Fir (Lund 1929a) are taken as an example.

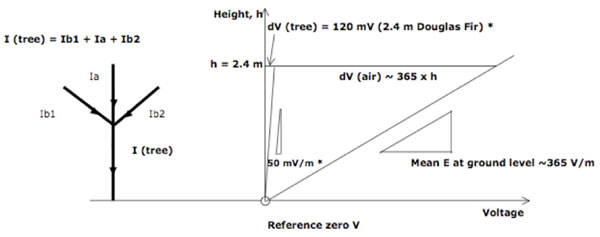
Figure 2: Currents and Potentials in tree and air paths. Some current will pass along the apex (Ia) and all the branches (Ib) to the main trunk of the tree. The currents through the tree I(tree) cause a potential gradient ( = Electric Field Intensity) dV(tree) in the tree but this is small compared to the normal atmospheric potential gradient of ~365 V/m in the air adjacent to the tree. Therefore as the tree grows higher, the potential difference dV(air) between the top of the tree and the air at that height increases significantly, enabling the tree to pass more current and hence generate a stronger internal potential gradient. V = Voltage; I = Current; E = Electric Field Intensity (=potential gradient) in Volts / meter; dV(tree) = Voltage drop over height of tree*; dV (air) = the potential difference between the top of the tree and the air at that height. * potential measurements in 2.4m tall Douglas Fir (Lund 1929a) are taken as an example.

 

The shape of leaves may also be expected to increase the current through the tree. It is well-known that charge concentrates on sharp points and, as we have seen, the tree is charged by contact with the Earth. Conifer needles and cones are known to act as charge concentrators which will enhance the electric field immediately adjacent to their surfaces (Aubrecht Stanek & Koller 2001); it seems likely that trichomes and points on the sharp edges of angiosperm leaves may have a similar function.

The effect of these localized concentrations of the electric field in the air immediately adjacent to the leaf surfaces is to increase the electric discharge from the leaf surfaces to the air, and hence to increase the total current through the tree which once again increases the potential gradient along the tree.

Thus it appears possible that the vertical atmospheric electric field may influence the electrical potential gradients in trees. If so, it should be expected that external factors may correlate to the observed daily and seasonal variations in potential within the tree. There is some evidence that this is the case.

The Earth’s field is not constant. Scrase (1934) quoted in Chalmers (1950) demonstrated that the Earth’s vertical electric field underwent two cycles of maxima and minima daily. Trees also exhibit diurnal variations in electrical potential and other characteristics. For example, Fraser-Smith (1978) demonstrated that Ultra-Low Frequency (ULF) variations in potential in quercus lobata “…were largely induced by ULF time variations of the geomagnetic field.” (Fraser-Smith 1978, p641).

Furthermore, Canny et al. (2007) have demonstrated that the Volumetric Water Content of the sapwood of Pinus contorta Douglas ex Loudon undergoes daily variations (ibid. Figs. 7 & 8) which appear to be the inverse of the Scrase (1934) (reproduced in Chalmers, 1950, Fig. 10) curves of diurnal variation of the Earth’s vertical electric field This appears suggestive of a link between the field and a tree’s response to that field, which may perhaps be modulated by the mechanism hypothesized in this paper.

Corollaries Of The Postulated Electrical Force Mechanism

a. Cavitation would not necessarily be fatal to the flow because the electrical force acts directly on the negatively-charged core sap whether or not there are embolisms in the xylem. Each element of core sap is supported independently, analogously to a bucket wheel. This mechanism may be relevant during the re-filling of xylem vessels in the spring (see e.g. Sperry et al 1988) and during development of alternative hydraulic pathways in plants subject to the double overlapping sawcut experiment during which the leaves did not wilt (Schulte & Costa 2010 and references therein).

b. If the tree’s metabolism alters the proton concentration in the positive annulus in any one cross-section of xylem then Coulomb forces will tend to ensure that negative charges are drawn into or repelled from the core region in order to maintain neutrality in the cross-section as a whole. Metabolic proton transfer, possibly via the xylem VAC and phloem companion cells as demonstrated by Fromard et al (1995), would then modify the electrical force on each element of sap. Local control of nutrient delivery mediated by proton transfer then becomes a possibility.

c. Embolisms could be closed by this mechanism if the core sap below an embolism received an increased electrical force due to an increase in negative ion concentration mediated by proton transfer. The additional upward force would result in an increase in pressure in the embolism above which would increase the chances of it being reabsorbed and the increased pressure could also drive flow upwards above the embolism if flow through the pore walls was limited.

d. The internal electric field would act in the opposite direction on any positive ions in the tree. Therefore the internal electric field would provide an additional driving force for the sucrose molecules in the phloem if they attract positive charge by preferential hydration bonding with either Hydronium ions or protons, as suggested by Johnson & Canny (2013).

Further Corollaries Of The Possible Influence Of The Earth’s Vertical Field

e. Rain or fog reduces the availability of highly mobile small ions in the air, which are attracted to the raindrops (Chalmers 1950, p33). Therefore the conductivity of the air will be reduced during periods of rain and this in turn may be expected to reduce the current through the tree. This may explain Fensom’s findings that the potential difference fell rapidly at the onset of rainfall. (Fensom 1963a)

The fact that exceptionally tall trees such as sequoia sempervirens are only found in fog-prone coastal habitats might seem to be contrary to the current hypothesis but it seems possible that Zimmermann D. et al’s (2007) explanation of foliar absorption during foggy periods may be paired with electrically-assisted water uptake from the ground in dry and sunny periods to provide the trees with a strategy for either condition.

f. Jayaratne, Ling & Morawska (2011) have postulated that trees transport radon from the ground and release it to the atmosphere, thereby increasing the ion concentration above forested areas. Additional ionisation will tend to reduce the resistance of the air, leading to an increase in the air-Earth current through the tree and hence an increase in the potential drop along the tree. By transporting radon, trees may be actively enhancing the supporting electrical force on the xylem sap.

g. It is possible that the suggested mechanism may provide some insight into the question posed by Wegner & Zimmermann (1998): “.. it is crucial to find a plausible explanation for the observation that the changes in the trans-root potential preceded changes in the xylem pressure of the root by about 1-3 min upon an increase in light intensity.” (Wegner & Zimmermann 1998, p863)
If the effect of increased illumination was to increase the current to air from the leaves in a manner analogous to the photoelectric effect in metals then an explanation of the observed effect may be within reach.

h. Barlow & Fisahn (2012) have observed daily fluctuations in the water volume fraction of Pinus contorta. The authors postulated that the variations might be related to the lunisolar gravitational fluctuations. However, as Canny has observed (private communication), their data might be better correlated to the diurnal variations of the Earth’s vertical electric field (Scrase, 1934 quoted in Chalmers 1950).

i. Tanner & Beevers (1990) found that there was no correlation between growth rates and transpiration rates in maize and concluded that “transpiration is not essential for long-distance transport of mineral elements in plants” (ibid. p745); the mechanism postulated here would allow transport of nitrate ions without transport of sap if the stomata were closed and effectively limited the flow of water molecules; in this case, the negative ions would move through the water, not with the water.

 

Future Research

The relationship between the known axial potential gradients and sap ascent in trees should be re-investigated, building on the pioneering work by Lund, Fensom and others, and considering the effect of the Earth’s electric field as summarized in this paper. It is vital that experiments are carried out on whole living trees, not on cut specimens or sections cut from trees and isolated from the Earth’s electric potential.

A key requirement of the hypothesis presented here is the separation of charge in the xylem sap into a positive annulus adjacent to the walls and negative core in the centre of the lumen. Identification of negatively-charged sap in the core may be considered to be an experimentum crucis for this hypothesis. Non-invasive techniques will be required in order to ensure that the experiment does not disturb the postulated charge separation in living, transpiring trees.

Measurements of potential in the tree must also be carefully designed to avoid unwanted electrical effects from the equipment itself operating in the Earth’s vertical electric field. Measurements of the natural vertical field and weather conditions should also be recorded simultaneously in order to gather further evidence for the apparent correlations between external factors and the internal potential of the tree.

 

Conclusions

The hypothesis presented above amounts to an argument in favor of adding an effective electrical term to the chemical potential equation when applied to xylem sap.

The proposed mechanism does not rely on metastable thermodynamic states of water, nor does it rely on tall trees having to “operate near the point of catastrophic xylem dysfunction” as Tyree et al. (1988) concluded was the case under the Cohesion Theory model.

Instead, the proposed mechanism relies on long-known electrical potential gradients in living trees together with recent research which has identified 100-micron-scale radial charge separation within water-filled tubes. This combination could allow for the electrical force on positive and negative ions in the xylem sap to be modulated in different ways, thereby assisting the ascent of the predominantly negative nutrients in the sap together with Hydrogen-bonded water molecules.

We have suggested that electrical forces can provide an efficient means of countering the gravitational force on xylem sap. The Earth’s natural vertical electric field may also be significant. Tall trees might simply be exploiting their electrical environment. It would perhaps be surprising if they did not take advantage of this free source of energy.

As Burr concluded as far back as 1947: “Attention should be called to the fact, however, that there is a growing body of evidence supporting the thesis that biological systems are, in certain senses of the word, electrical machines.” (Burr 1947, p317)

 

Acknowledgements

The author would like to thank Martin Canny for his help and encouragement to write this paper, and Jim Johnson and the staff at The Friday Harbour Laboratories Library for their help in obtaining copies of some of Lund’s key papers used in this research. The author confirms that there are no conflicts of interest regarding this work.

 

References

Amin M (1982) Ascent of sap in plants by means of electrical double layers. Journal of Biological Physics 10, 103–109

Aubrecht L, Stanek Z, Koller, J (2001) Corona discharge on coniferous trees-spruce and pine. Europhysics Letters 53(3), 304–309

Balling A, Zimmermann U (1990) Comparative measurements of the xylem pressure of Nicotiana plants by means of the pressure bomb and pressure probe. Planta 182, 325-338

Barlow PH, Fisahn J (2012) Lunisolar tidal force and the growth of plant roots, and some other of its effects on plant movements. Annals of Botany 110 (2), 301-318

Burr HS (1945) Diurnal potentials in the maple tree. Yale Journal of Biology and Medicine 17, 727-735

Burr HS (1947) Tree potentials. Yale Journal of Biology and Medicine 19 (3), 311-318

Canny MJ, Sparks JP, Huang CX, Roderick ML (2007) Air embolisms exsolving in the transpiration water – the effect of constrictions in the xylem pipes. Functional Plant Biology 34, 95–111

Chalmers JA (1950) Atmospheric Electricity. 2nd Ed Oxford University Press, London

Crews LJ, McCully ME, Canny MJ (2003) Mucilage production by wounded xylem tissue of maize roots – time course and stimulus. Functional Plant Biology 30(7), 755 – 766

Dixon HH, Joly J (1895) On the Ascent of Sap. Philosophical Transactions of the Royal Society London B 186, 563-576

Fensom DS (1957) The bio-electric potentials of plants and their functional significance: I. An electrokinetic theory of transport. Canadian Journal of Botany 35(4), 573-582

Fensom DS (1958) The bio-electric potentials of plants and their functional significance: II. The patterns of bio-electric potential and exudation rate in excised sunflower roots and stems. Canadian Journal of Botany 36(3), 367-383

Fensom DS (1959) The Bio-Electric Potentials of Plants and Their Functional Significance: III. The Production of Continuous Potentials Across Membranes in Plant Tissue by the Circulation of the Hydrogen Ion. Canadian Journal of Botany 37(5), 1003-1026

Fensom DS (1962) The bio-electric potentials of plants and their functional significance: IV. Changes in the rate of water absorption in excised stems of acer saccharum induced by applied electromotive forces: the «flushing effect». Canadian Journal of Botany 40(3), 405-413

Fensom DS (1963a) The bio-electric potentials of plants and their functional significance: V. Some daily and seasonal changes in the electrical potential and resistance of living trees. Canadian Journal of Botany 41(6), 831-851

Fensom DS, Dainty J (1963b) Electro-Osmosis in Nitella. Canadian Journal of Botany 41(5), 685-691

Fraser-Smith AC (1978) ULF tree potential and geomagnetic pulsations. Nature 271, 641–642

Fromard L, Babin V, Fleurat-Lessard P, Fromont J-C, Serrano R, Bonnemai J-L (1995) Control of Vascular Sap pH by the Vessel-Associated Cells in Woody Species: Physiological and Immunological Studies. Plant Physiology 108, 913-918

Gibert D, Le Mouël J-L, Lambs L, Nicollin F, Perrier F (2006) Sap flow and daily electric potential variations in a tree trunk. Plant Science 171, 572–584

Gindl W, Löppert HG, Wimmer W (1999) Relationship between Streaming Potential and Sap Velocity in Salix alba L. Phyton (Horn, Austria) 39 (2), 217-224

Gollan T, Schurr U, Schulze E-D (1992) Stomatal response to drying soil in relation to changes in the xylem sap composition of Helianthus annuus I. The concentration of cations, anions, amino acids in, and pH of, the xylem sap. Plant, Cell and Environment 15, 551-559

Holbrook NM, Zwieniecki MA (1999) Embolism Repair and Xylem Tension: Do We Need a Miracle? Plant Physiology 120, 7–10

Jayaratne ER, Ling X, Morawska L (2011) Role of Vegetation in Enhancing Radon Concentration and Ion Production in the Atmosphere. Environmental Science Technology 45 (15) A-F

Johnson RJ, Canny MJ (2013) Phloem Translocation of Organic Compounds: A Possible Mechanism to Assist Osmotically- Generated Pressure Flow in Tall Trees. WATER Journal 4, 112-128

Klyuzhin I, Symonds A, Magula J, Pollack GH (2008) A new method of water purification based on the particle-exclusion phenomenon. Environmental Science and Technology 42(16), 6160-6166

Koppán A, Fenyvesi A, Szarka L Wesztergom V (2000) Annual fluctuation in amplitudes of daily variations of electrical signals measured in the trunk of a standing tree. Comptes Rendus de l’ Académie des Sciences, Paris, Sciences de la Vie/Life Sciences, Series IIa 323, 559–563

Koppán A, Fenyvesi A, Szarka L, Wesztergom V (2002) Measurement of electric potential difference on trees. Proceedings of the 7th Hungarian Congress on Plant Physiology, 2002: Acta Biologica Szegediensis 46(3-4), 37-38

Le Mouël J-L, Gibert D, Poirier J-P (2010) On transient electric potential variations in a standing tree and atmospheric electricity. Comptes Rendus Geoscience 342, 95–99

Lund EJ (1925) Experimental Control Of Organic Polarity By The Electric Current. V. The Nature Of The Control Of Organic Polarity By The Electric Current. The Journal of Experimental Zoology 41 (2), 155-190

Lund EJ (1928a) Relation Between Continuous Bio-Electric Currents And Cell Respiration. II. The Journal of Experimental Zoology 51(3), 265-290

Lund EJ (1928b) Relation between continuous bio-electric currents and cell respiration. V. The quantitative relation between Ep and cell oxidation as shown by the effects of cyanide and oxygen. The Journal of Experimental Zoology 51(3), 327-337

Lund EJ (1929a) Electric Polarity in the Douglas Fir. Puget Sound Biological Station, University of Washington 7, 1-28.

Lund EJ (1929b) The relative electrical dominance of growing points in the Douglas Fir. Puget Sound Biological Station, University of Washington 7, 29-37.

Lund EJ (1930a) Internal distribution of the electric correlation potentials in the Douglas Fir. Puget Sound Biological Station, University of Washington 7, 259-287.

Lund EJ (1931a) The unequal effect of O2 concentration on the velocity of oxidation in loci of different electric potential and glutathione content. Protoplasma 13, 239-258

Lund EJ (1931b) External Polarity Potentials In The Apex Of The Douglas Fir Before And After Mech-anical Stimulation. Plant Physiology 6(3), 507-517

Lund EJ (1931c) Electric correlation between living cells in cortex and wood in the Douglas fir. Plant Physiology 6, 631-652

Lund EJ (1932a) Control of the flux equilibrium of electrochemical processes and electric polarity in the Douglas fir by temperature. Plant Physiology 7, 297-307

Lund EJ (1932b) Comparison of the effects of temperature on the radial and longitudinal electric polarities in wood and cortex of the Douglas fir. Plant Physiology 7, 505-516

Lund EJ, Bush M (1930b) Electric Correlation Potentials in the Leaf of Bryophyllum. Plant Physiology 5(4), 491-508

Lund EJ, Kenyon WA (1927) Relation Between Continuous Bio-Electric Currents And Cell Respiration. I. Electric Correlation Potentials In Growing Root Tips. The Journal of Experimental Zoology 48(2), 333-357

Meinzer FC, Clearwater MJ, Goldstein G (2001) Water transport in trees: current perspectives, new insights and some controversies. Environmental and Experimental Botany 45, 239–262

Morat P, Le Mouël JL, Granier A (1994) Electric potential on a tree. A measurement of the sap flow? Comptes Rendus de l’Académie des Sciences, Paris, Sciences de la Vie/Life Sciences 317, 98–101

Nobel PS (2005) Physicochemical and Environmental Plant Physiology. 3rd Edition, Academic Press Inc, pp59-61

Plumb RC, Bridgman WB (1972) Ascent of Sap in Trees. Science, New Series 176(4039), 1129-1131

Rosene HF (1937) Effect of an Applied Electric Current on the External Longitudinal Polarity Potentials of Douglas Fir. American Journal of Botany 24 (6), 390-399

Schulte, PJ Costa, DG (2010) Xylem anisotropy and water transport—a model for the double sawcut experiment. Tree Physiology 30, 901–913

Scrase FJ (1934) Observations of atmospheric electricity at Kew Observatory: a survey of results obtained from 1843 to 1931. Meteorological Office, HMSO, London, UK: Geophysical Memoirs 60

Sperry JS (2003) Evolution of Water Transport and Xylem Structure. International Journal of Plant Sciences 164 (3), S115–S127

Sperry JS, Donnelly JR, Tyree MT (1988) Seasonal occurrence of xylem embolism in sugar maple (Acer saccharum). American Journal of Botany 75, 1212-1218

Tanner W, Beevers H (1990) Does transpiration have an essential function in long-distance ion transport in plants? Plant, Cell and Environment 13, 745-750

Tyree MT (1997) The cohesion–tension theory of sap ascent: current controversies. Journal of Experimental Botany 48, 1753–1765

Tyree MT, Sperry JS (1988) Do woody plants operate near the point of catastrophic xylem dysfunction caused by dynamic water stress? Answers from a model. Plant Physiology 88(3), 574–580

Volkov AG (Ed) (2012) Plant Electrophysiology. Springer-Verlag Berlin Heidelberg

Wegner LH, Zimmermann U (1998) Simultaneous recording of xylem pressure and trans-root potential in roots of intact glycophytes using a novel xylem pressure probe technique. Plant, Cell and Environment 21, 849-865

Westhoff M, Schneider H, Zimmermann D et al (2007) The mechanisms of refilling of xylem conduits and bleeding of tall birch during spring. Plant Biology 10, 604-623

Zheng JM, Pollack GH (2006) Solute exclusion and potential distribution near hydrophilic surfaces. In Water and the Cell (eds G H Pollack, I L Cameron D N Wheatley) pp165-174. Springer, Dordrecht, The Netherlands

Zimmermann D, Westhoff M, Zimmermann G et al (2007) Foliar water supply of tall trees: evidence for mucilage-facilitated moisture uptake from the atmosphere and the impact on pressure bomb measurements. Protoplasma 232, 11-34

Zimmermann U, Meinzer FC, Benkert R, Zhu JJ, Schneider H, Goldstein G, Kuchenbrod E, Haase A (1994) Xylem water transport: is the available evidence consistent the cohesion theory? Plant, Cell and Environment 17(11), 1169-1181

Zimmermann U, Wagner H-J, Schneider H (2000) Water Ascent in Plants: the Ongoing Debate. Trends in Plant Science 5(4), 145-146

Zimmermann U, Schneider H, Wegner LH, Wagner H-J, Szimtenings M, Haase A, Bentrup F-W (2002a) What are the driving forces for water lifting in the xylem conduit? Physiologia Plantarum 114(3), 327–335

Zimmermann U, Wagner H-J, Heidecker M, Mimietz S et al (2002b) Implications of mucilage on pressure bomb measurements and water lifting in trees rooting in high-salinity water. Trees 16, 100–111

Zimmermann U, Schneider H, Wegner LH, Haase A (2004) Tansley review. Water ascent in tall trees: does evolution of land plants rely on a highly metastable state? New Phytologist 162, 575–615

 

Discussion with Reviewers

R. Johnson: The reviewer raises some interesting and important points and the author thanks him for his careful consideration of the current paper and for drawing attention to various papers of his own in which detailed mathematical analyses of the ascent of sap are presented.

The author of the present paper is pleased to note in particular that the reviewer states that ‘the disjoining pressure can take account of the electric field’ which implies that the electrical effects investigated in detail in the present paper are compatible with the rigorous mathematical analyses presented by the reviewer. Turning to the particular points the reviewer raises, there are three questions and a more general point regarding the disjoining pressure. I will deal with each of these in turn.

M. Gouin, Reviewer: The author said: transpiration is not essential for long-distance transport of mineral elements in plants…, the negative ions would move through the water not with the water. Why this result is not true in all the cases?

Johnson: The first part of the question is a quote from Tanner & Beevers (1990); the remainder of the first sentence is from the author’s suggested explanation of this finding. The paragraph in question is presented as a corollary of the postulated mechanism. The explanation offered stated in full: “..the mechanism postulated here would allow transport of nitrate ions without transport of sap if the stomata were closed and effectively limited the flow of water molecules; in this case, the negative ions would move through the water, not with the water.”

The essence of the postulated mechanism is that electrical forces act directly on the negative ions in the sap in the core region of the xylem. During transpiration, hydrogen bonding between the negative ions and the surrounding water molecules tends to drag neutral water molecules along with the negative ions. As stated earlier in the paper “The effect is similar to viscous drag as observed in electro-osmotic flow.”

Clearly, the transported water is transpired from the leaves and so allows more sap to flow up the xylem. This is analogous to an open tap on the end of a pipeline.

However, when the tap is shut off, i.e. when transpiration ceases, no more sap can flow but the electrical forces are still present for as long as the longitudinal voltage gradient remains in the plant. In this case, the negative ions will be forced through the surrounding sap, similar to the way a bubble ascends through a stationary liquid.

Reviewer: The proposed mechanism does not rely on metastable thermodynamic states of water, nor does it rely on tall trees having to operate near the point of catastrophic xylem dysfunction. Why the trees do not have a limit height in the model? It seems no limit can be forecasted.

Johnson: The range of heights of trees, even within the same species, suggests that the height to which a tree grows is a function of numerous different variables. Whilst it is suggested in this paper that trees take advantage of their electrical environment by growing higher, nevertheless there are obvious costs to doing so.

One of the most significant factors is structural; the tree must be able to withstand wind pressure in normal climatic conditions. One would expect there to be a natural limit representing the balance between the benefits of height and the cost of the structure; this balance point differs for each species.

Whether there is a maximum height limit dependent of the function of the xylem is a question not addressed in this paper. M. Gouin has suggested that mathematical analyses of fluid layers in the xylem indicate a maximum limit of 140m for “less hydrophilic surfaces” with a Young’s Contact Angle of 50º; this figure is derived from work on carbon nanotubes. [arXiv:1204.4094 & arXiv:0809.3529].

If this figure is also representative of the hydrophobic xylem as M. Gouin suggests then the question appears to be adequately answered by the reviewer’s own work and perhaps needs no further elaboration here.

Reviewer: No calculation and/or equation justifying the role of electric forces are presented, could you elaborate on this?

Johnson: I freely admit that I have to rely on others much better qualified than myself in applied mathematics to supplement my conceptual work with more rigorous analyses and I would welcome M. Gouin’s input should he be inclined to investigate my proposals further.

By way of a token mathematical contribution in support of the section in the current paper headed ‘Quantification of the proposed effect’, I offer the following additional details of the calculation of the stated figure of 2.08 mol/m3 of singly-ionized molecules in the core sap being all that is necessary to support the sap:

This figure is derived as follows:
Weight of 1 m3 of sap, W ≈ 104 N

Electric force Fe on a singly-charged ion due to E = 50mV/m,
Fe = E x q = 50 x 10-3 x -1.6 x 10-19 = -8 x 10-21 N

Number density of negative ions necessary to balance weight of sap,
n = |W/Fe| = 1.25 x 1024 per m3

Therefore the required molar ion concentration to support the weight of water molecules in sap by E of 50mV/m= n / NA = n / 6 x 1023 = 2.08 mol / m3

The origin of the figure for the electric field strength E used above is described in the text; q is the charge on an electron or singly-charged negative ion in Coulombs; NA is the Avogadro Constant.

The point is that the actual nitrate concentration in the xylem sap may be in the region of 7.33 mol / m3 and therefore more than sufficient to meet the requirements of the current hypothesis.

Reviewer: The disjoining pressure can take account of the electric field (as it is done in the physical chemistry literature by the Russian school of Derjaguin et al.: see references).

Johnson: I pointed out above that this implies that the electrical effects investig-ated in detail in the present paper are compatible with the rigorous mathematical analyses presented by the reviewer, which is most gratifying, but some additional comment is clearly expected.

The disjoining pressure represents the spatial gradient of the Gibbs Free Energy per unit area due to the interaction between a liquid and a solid surface; it also represents the difference between the pressure in the surface layer and the pressure in the bulk liquid. In a vertical layer such as on the xylem wall, M. Gouin’s analyses show that the disjoining pressure is related to the volume free energy i.e. the integral of the chemical potential in the interface layer. See for example p10 of A new approach for the limit to tree height using a liquid nanolayer model (Gouin 2008).

The current paper concludes: “The hypothesis presented above amounts to an argument in favor of adding an effective electrical term to the chemical potential equation when applied to xylem sap.” The reviewer’s assertion that the disjoining pressure can take account of the electric field appears to be a restatement of this paper’s conclusion.

However, M. Gouin’s mathematical analyses do not appear to contain any suggestion as to exactly how such electrical forces are manifested in the ascent of sap.

What the current paper offers is a mechanism whereby these electrical effects come into play. In other words, the current hypothesis suggests a reason as to why electrical forces should be included in the chemical potential equation, thereby complementing the mathematical analyses presented by the reviewer.

 

DWR References

Gouin H (2008) A new approach for the limit to tree height using a liquid nanolayer model. Continuum Mechanics and Thermo-dynamics 20, 317-329

Gouin H (2009) A mechanical model for the disjoining pressure. International Journal of Engineering Science 47, 691-699

Gouin H (2011) Liquid-solid interaction at nanoscale and its application in vegetal biology. Colloids and Surfaces A 383, 17-22

Further comments can be found in: arXiv: 1204.4094

Close Menu