 The Source of Some of the Extraordinary Powers and Properties of Enzymes
The Source of Some of the Extraordinary Powers and Properties of Enzymes
Wiggins P1
1*Retired from the Department of Medicine, University of Auckland, New Zealand, and from Genesis Research and Development Company, Auckland, New Zealand.
Correspondence: p.wiggins@paradise.net.nz
Key Words: protein folding, water activity in solutions
Received 26 September 2008; revised 6 November 2008; accepted 5 January 2009. Published 1 July 2009. Available online 1 July 2009.
Summary
The generally successful model of liquid water, with its range of hydrogen bond strengths from weak to strong, fails to account for much of biochemistry. In particular it cannot supply the compensating decrease in free energy required to balance decreases in entropy in well-explored processes such as protein folding in solution. A simplified model in which there are just two strengths of hydrogen bonds seems to account as well for the broad bands of the vibrational spectrum of water, and at the same time has an inbuilt reservoir of free energy which can be harnessed to balance the decrease in entropy and increase of complexity of so many biochemical processes.
Article Outline
- Introduction
- The Alternative Assumption
- Protein folding in LDW/HDW
- Problems with Current Views of Protein Folding
- Specificity
- The Size of Enzymes
- Isolated HDW
- LDW
- RNA
- Conclusions
- Acknowledgments
- References
- Discussion with Reviewers
Introduction
The generally accepted and used model of liquid water (classical water) is based on the assumption that there is a range of hydrogen-bond strengths from very weak to strong (for a hydrogen bond). This assumption was made to explain the infra red and Raman spectra (Eisenberg and Kauzmann, 1969). The outstanding property of these vibrational bands of water is that they are extremely broad. Obviously, a single hydrogen bond strength is not possible because that would produce sharp, narrow bands.
The prevailing assumption has proved useful: with a few anomalies (Vedamuthu et al (1994) Cho et al (1997) it agrees with most of the observed properties of liquid water. It had been accepted and used for some time before biochemists adopted it. Biochemists, of course, had no choice but to accept the implicit assumption, made by water scientists themselves. It was, in fact, no longer considered an assumption but a factual aspect of the theory of water structure. The result of this has been that biochemists have, rightly, largely ignored water in their elucidations of biochemical mechanisms. Instead, they have invented ingenious mechanisms relying on assumed unique properties of enzymes. Thus biochemistry has become a patchwork of ad hoc assumptions of specific binding sites for small molecules and ions.
In retrospect it appears that a biochemist has had to operate with one hand tied behind his back, merely because it seemed to be no part of his job description to question the conclusions of water physicists and chemists. It also appears in retrospect and in prospect that biochemistry is the most demanding and informative testing ground for water chemistry. The intention of this article is to account for some of the truly remarkable properties of enzymes by employing a single assumption concerning the structure of liquid water. This is not an arbitrary assumption; it is an alternative to the existing assumption on which water chemistry appears to be firmly based. It has been shown to fill many of the gaps in biochemistry. (Wiggins, 2002, 2007, 2008a 2008b)
The Alternative Assumption
To return to the vibrational spectrum of water, there is a second possible interpretation of the broad bands: namely, that there are two strengths of water-water hydrogen bonds, one weak and one strong and that the resulting overlapping bands appear as a single broad band. Analysis of the FTIR spectra should reveal whether two single values of H-bond strength are adequate or whether two separate tight clusters about a low and a high value are needed. Some of the consequences of this model of coexisting microdomains have already been described (Cho e al (1997) Vedamuthu et al (1994). Low density water (LDW) has strong, straight H-bonds and a density of 0.91 g/ml. High density water has bent, weak H-bonds and a density of 1.2 g/ml.). Since their hydrogen bond strengths are different, all physical and chemical properties of the two microdomains differ, including their solvent properties.
The most important consequence of the coexistence of the two microdomains is that any solution in such water has an inbuilt reservoir of free energy that can be harnessed for assembly of solute molecules into ordered arrays. Examples are: folding of proteins, the double helix of DNA, the triple helix of collagen, the formation of double layers and micelles from long-chain fatty acids, the aggregation of biopolymers into higher-ordered arrays. All these processes happen spontaneously and yet it is not always obvious how the large decrease in entropy is balanced by a decrease in free energy somewhere else in the system. In fact, a fundamental property of biology is that it increases order and complexity and decreases entropy in sometimes still mysterious ways. The aim here is to dispel that mystery.
The source of the reservoir of energy is illustrated in Figure 1, in which it is shown that any solute which dissolves in water generates a pressure gradient, positive at the immediate surface of the solute and negative further out. If the water is ‘classical’ water, this gradient has no effect because it is assumed that classical water is impervious to the low pressures encountered in osmotic systems. If the water is the mixture of microdomains (LDW/HDW) the solute dissolves either in LDW when the pressure gradient generates extra HDW or in HDW when the pressure gradient generates more LDW.
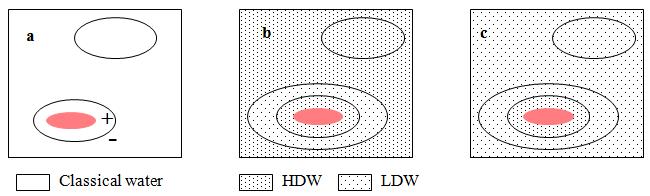
Figure 1: A small solute (red) has dissolved in (a) “classical water,” (b) HDW, and (c) LDW. In each case, water immediately adjacent to the solute has a lower concentration (activity) than the same volume away from the solute. This activity gradient results in a pressure gradient, which is positive immediately adjacent to the solute and negative further away. a, nothing happens because “classical” water is assumed to be impervious to the low pressures encountered in osmotic systems; b, water immediately adjacent to the solute is already HDW and is not further affected, but where the pressure is negative, a zone of HDW is converted to LDW; c, the positive pressure immediately adjacent to the solute converts some LDW into HDW, while the negative pressure has no further effect upon LDW.
Figure 1 shows that any solute that dissolves in the water mixture (LDW/HDW) shifts the equilibrium in one direction or the other, thus incurring a thermodynamic cost. This cost is not symmetrically distributed between HDW and LDW because it always includes a PDV term, which is positive going from HDW to LDW and negative in the opposite direction. If the free energy of solution is DGs then it has four components:
ΔGs =ΔGm + ΔGw + ΔGl + ΔGh
where ΔGm is the free energy of mixing and is always large and negative, ΔGw is the positive change due to shifting of the water equilibrium, ΔGl is the positive term of removing the solute from the crystal lattice and ΔGh is the negative free energy of hydration of the solute, its absolute value depending upon the specificity of the solute. It is ΔGw which acts, in a sense, as a reservoir of energy.
Protein Folding in LDW/HDW
Suppose that the solute in Figure 1 was a large protein which was predominantly hydrophobic. As it emerged from a ribosome it partitioned into HDW. Although no protein has a large partition coefficient between HDW and LDW, the molecule, itself in its unfolded, extended configuration, has a very large surface in contact with HDW, and is responsible for a considerable increase in the fraction of LDW at the expense of HDW (see Figure 1b). Therefore, as it dissolved in HDW, ΔGw was large and positive so that the protein was probably insoluble in its extended conformation. If, however, one regards “solution and folding of the protein” as a unitary process, folding is an essential part of overall dissolution. As it proceeds, folding diminishes the surface area in contact with water and diminishes ΔGw. Thus the free energy of the product (folded protein in solution) is lower than the free energy of the reactant (extended protein in solution or not) and the reaction will go spontaneously. Here there is no mystery. And no further assumptions need be made. It is the collective action of water molecules that decrease the free energy of the whole system (water, protein and other solutes) while the entropy of the protein is decreasing (Wiggins, 2008a and 2008b).
In classical water ΔGw is zero. Furthermore, in classical water, the size of the solute is not important: the decrease in water activity depends only upon the number of solute species and the unitary process is solution of the extended form of the protein. This may appear preferable, but there is nothing left to drive folding of the protein. If it folds (which in practice it always does) it must be assumed that the act of folding generates enough decrease in free energy by means of amino acid-amino acid interactions to compensate for the large decrease in entropy. Many ad hoc assumptions of binding forces between amino acids are needed. When the protein is predominantly hydrophobic, some folding is attributed to the “hydrophobic effect”: i.e. to the belief that hydrophobic patches of surface “hate water” and squeeze it out. The “hydrophobic effect” is just a single example of the ability of folding to decrease the area of contact between protein and water and thus decrease ΔGw. Therefore, although the hydrophobic effect is well-documented experimentally, it has no real explanation in classical water. “Hydrophobic” solutes do not hate water; they have an inordinate love of HDW into which they partition highly selectively. All observed properties of hydrophobic molecules (except their name) can be accounted for in these terms, adding considerable weight to the alternative assumption.
A predominantly hydrophilic protein also folds first to helices or pleated sheets with opportunistic hydrogen bonds, and then by a non-specific apparent stickiness of hydrophilic surfaces. Experiments with glass beads (44-500 mm in diameter) (Wiggins (2007) illustrated the strength of this non-specific stickiness. Beads could be made hydrophobic, or used as they were (hydrophilic). It was found that hydrophobic beads stuck to both hydrophilic and hydrophobic surfaces, and that hydrophilic beads also stuck to both hydrophilic and hydrophobic surfaces. It became clear that this universal stickiness was simply a way of decreasing the water/surface contact and thus lowering the system free energy.
Problems with Current Views of Protein Folding
There are real problems with the usual treatment of protein folding. If water has its generally assumed configuration of a wide range of hydrogen bond strengths, it is extremely unlikely that the folded protein should have a lower free energy than the same protein in its extended conformation. And yet the progress of folding is depicted as a funnel leading to a minimum in free energy, specifically of the protein (Chaplin (2006)). There is no doubt that a protein does fold spontaneously to a singular state, but that state is not a state of minimal free energy of the protein. It is a state of minimal free energy of the whole system. The protein is a single component of the solution, and cannot be treated as if it were in isolation. Thermodynamics is satisfied if the decrease in entropy of the protein on folding is matched by a decrease in free energy somewhere else in the system: in this case, specifically, in a decrease in DGw. Chaplin (2006) describes the role of individual water molecules in easing the folding and accelerating it. This is excellent for the kinetics of the process but does nothing for the thermodynamics.
Specificity
Every solute so far investigated partitions selectively into HDW or into LDW. It follows that there is an affinity between any solute and either HDW or LDW. Therefore in Figure 1 the configurations are changed by this specific contribution of the solute.
If the solute has an affinity for HDW (eg. hydrophobic molecules and small cations such as Na+, Li+, H+, Ca2+, Mg2+, and L-glucose, D-amino acids) it will attract some HDW to its surface, increasing the amount of HDW. If, however, the solute has an affinity for LDW (eg. K+, most anions and D-glucose and L-amino acids} it cannot generate LDW immediately at the surface because that region is under positive pressure. It follows that water immediately adjacent to a surface is always HDW, irrespective of the particular properties of the surface.
The Size of Enzymes
Enzymes are always large (100,000 is an average molecular weight}. But they always decrease their physical size by folding and, when folded, it appears that only a very few surface groups are involved in the reaction catalyzed by the enzyme. Why are they so large? This is one of the many biochemical puzzles that has survived unexplained by classical water. Formation of a peptide bond between two amino acids does not take place spontaneously in a cell. It requires ATP hydrolysis or dissipation of an expensively formed ion gradient. Synthesis of a protein of MW 100,000, therefore, uses much precious energy. Once it is formed the protein folds to reduce its size, again using energy. This appears a profligate waste. Is there not an easier/cheaper way of bringing the few participating groups together? To one attuned to the messages of Figure 1, the rationale is clear.
Energy has been used to generate a large soluble surface at which there is a stable zone of HDW perhaps 1-3 nm thick. Where this zone ends there is a stable zone of LDW, also 1-3 nm thick. Superimposed upon these zones are specific sites in which charged groups with counterions in solution generate their own pockets of HDW and LDW.(Wiggins, 2008a, 2008b) It might be said that these zones and pockets are the enzyme. They are large enough to accommodate substrates and cofactors with a specificity that leaves no need for a binding site, so that the resulting reaction takes place in either HDW or in LDW, or sequentially in one then the other. The combinations and permutations are many. Only a biochemist can decide the extent to which these pockets and zones of HDW and LDW contribute to the overall function of a given enzyme. Some possibilities are:
Isolated HDW
In HDW/LDW many properties of HDW are suppressed. For example, it is not permitted to boil at its intrinsic boiling point, which is probably well below 0oC (Wiggins (2007)) because that would leave an excess of LDW in residual water. The ionisation of water is also depressed in HDW/LDW because ionization produces two species which partition into HDW (H+ and OH–) thus increasing the shift of the water equilibrium toward LDW (see Figure 1b) and increasing ΔGw.
An. isolated pocket of HDW, however, such as that at the surface of a folded enzyme can act more independently because it now ‘belongs’ in some sense to the enzyme. When, with a diffusional jump, a protein sheds its associated zones of HDW and LDW, it immediately renews them in its next stationary position; so that, effectively, the zones have moved with it. Such a zone is no longer under the dominion of the HDW/LDW equilibrium. It forms spontaneously at the surface of the solute, and must obey the local conditions such as linkage to the similarly-formed zone of LDW. So, ionisation is permitted and HDW can be so reactive as to hydrolyse peptide bonds as it has the reactivity of both a strong acid and a strong base together, a formidable catalyst (Wiggins, 2007).
HDW is extremely fluid so that reactions which are diffusion-limited are greatly accelerated. This accounts for one of the principal attributes of enzymes.
LDW
LDW does not accelerate reactions because it is more viscous than LDW/HDW. It does, however, permit some reactions with positive free energy changes in LDW/HDW to go spontaneously. For example ATP, poly-L-lysine and poly-D-glucose have been made in our laboratory in LDW (Wiggins, 2007).
RNA
RNA, if it is big enough, is said to have enzyme-like properties, (Matthews and van Holde, 1990) suggesting that size is more important than composition for catalytic properties. This suggests the further possibility that polymer chemists might synthesize effective enzymes.
Conclusions
Protein folding with its large decrease in entropy absolutely requires a decrease in free energy somewhere else in the solution. This happens automatically in the simplified configuration of liquid water with only two strengths of hydrogen bonds, but is impossible in water with a range of hydrogen bond strengths. Again, in the simplified water, enzymes appear not to need specific binding sites for substrates and cofactors.
Acknowledgments
I am grateful to Mr. Ben Liebert for converting the figures to TIFF.
References
Chaplin M (2006). Do we underestimate the importance of water in cell biology? Nature Reviews Molecular Cell Biology.
Eisenberg D, Kauzmann W. (1969) The Structure and Properties of Water, p.199, Clarendon Press, Oxford.
Cho HC, Singh S, Robinson GW. (1997) Understanding all of water anomalies with a non-local potential. J Chem Phys 107: 7979-7988.
Matthews CK, van Holde KE (1990), Biochemistry, The Benjamn/Cummings Publishing Company, New York, 373.
Vedamuthu M, Singh S, Robinson GW (1994). Properties if liquid water: origin of the density anomalies. J Chem Phys 98: 2222-2230.
Wiggins PM (2002). Enzyme reactions and two-state water. J.Biol. Phys.Chem. 2: 25-37.
Wiggins, PM (2007). Life depends upon two types of water. PloS ONE 3 (1): e1406.
Wiggins, PM (2008). Prions, plaques and polyelectrolytes. J. Biol.Phys. Chem. 8: 49-54.
Wiggins PM (2008). DNA as a Darwinian self-replicator. J.Biol.Phys.Chem. 8: 89-93.
Discussion with Reviewers
James Clegg1: Do you mean the boiling point of HDW is below 0oC?
Philippa Wiggins: I do mean boiling point. I discussed this in my 2007 paper. It derives from a comparison with the boiling points of hydrides of elements close to O in the Periodic Table (HF, H2S, H2Se. H2Te} all of which boil at extremely low temperatures and are not mutually hydrogen bonded or, in the case of HF, extremely weakly hydrogen bonded. A plot of the boiling points of the three Group 6 hydrides extrapolated to a molecular weight of 18 predicts a boiling point for water of -75oC. The abnormally high BP of water (100oC) has been attributed to its hydrogen-bonding: it takes more energy to break those bonds and vaporise water than just to vaporise. It should follow, therefore, that isolated HDW with its weak H-bonds should have an intrinsic boiling point similar to the weakly bonded HF. Presumably -75oC is the boiling point of unbonded water.
I have spent many months experimenting with cellulose acetate membranes which are used as reverse osmosis membranes: i.e., if one applies a pressure to the solution side of such a membrane water moves through, leaving solutes behind. The water inside these membranes had the infra red spectrum of ice, not liquid water. Presumably that was LDW because the membranes did allow solutes in: the inside was clearly liquid. Nevertheless chlorides of Mg2+, Ca2+, H+, Li+, Na+ were somewhat excluded (Na+ least and Mg2+ most). At low concentrations K+ was accumulated. And yet, when these membranes were exposed to a pressure on the solution side, no ions got through. Water inside the pores was isolated from the bulk solution outside but subjected to the applied pressure. LDW was presumably converted to HDW, and then, being outside the dominion of HDW/LDW, it vaporised, dropping its solutes at the mouth of the pore. It then passed through the pore in the vapour state. Once through the membrane it condensed into the mix of HDW/LDW dictated by the prevailing temperature and pressure. I know of no other explanation for the mechanism of these membranes.
Carbon nanopores have also been shown to allow water through at remarkably high rates, consistent with the vapour phase.
Clegg: Given the presence of HDW and LDW, do these make up all the intracellular water? Or can there be “ordinary” water present?
Wiggins: If there are zones of HDW and LDW present intracellularly, that is “ordinary” water. The two assumptions are mutually exclusive: You have to make a choice. The only way to decide whether or not you have made the better choice is to explore the explanatory power past and future of each, both in biochemistry and in water chemistry.
Clegg: How about multi enzyme complexes and enzymes partially embedded/associated with cell structures such as membranes?
Wiggins: I have specified solubility here because I was peddling the power of the thermodynamics of aqueous solutions. But surfaces in contact with a solution play a part. Water immediately adjacent to an insoluble surface is in a state of lower activity than water further away. As with small solutes there is a pressure gradient inducing HDW at the surface and LDW further away. Insoluble surfaces contribute to ΔGw which may drive the two surfaces to ‘stick’ to each other. This is the driving force for the higher aggregations you mention. The reduction of ΔGw by nonspecific stickiness can lead to a state of extremely low entropy. Our glass bead experiments were undertaken with this kind of stickiness in mind. When we made the beads hydrophobic by methylating them and lowered them rather gently into water, they all stuck together in a single mass, in spite of the fact that they were all negatively charged. Moreover they floated on water, in spite of the fact that they had a density of 2.6 g/ml. Clearly this ΔGw amounts to a powerful force. The floating was due to retention of air, which was completely blocked by a zone of LDW round the beads. Unmethylated beads stuck together but did not float.
In the tiny world of biopolymers the power of DGW must rule.
Clegg: Is your thinking compatible with Gilbert Ling’s AIH or Drost-Hansens’s vicinal water?
Wiggins: Gilbert Ling and Drost-Hansen both rely as I did for many years on either H-bonding of water to water and water to surfaces or bonding of water in polarized multilayers. The trouble is that while water does make its strongest H-bonds with other water molecules, they are still very, very weak. It is hard to see how large-ish zones of H-bonded water or of polarized multilayers could have stability in the face of kinetic energy of various kinds. A solution is a very busy place. For that reason I spent a lot of time with polyamide beads which, like cellulose acetate films contained stable zones of LDW. This was a commercial preparation and the beads were calibrated by the size of molecules that they excluded. I calibrated them in terms of their ability to accumulate solutes which partitioned into LDW, particularly D-glucose. The smallest diameter was that of P-2 and was approximately 1-2 nm, P-4 was about 2nm and P-6 3nm and more. P-2 and P-4 accumulated glucose well. P-6 did slightly, but p-10 and larger diameters did not accumulate measurable amounts. Similarly cellulose acetate membranes lost their specificity when they swelled in solutions of solutes which partitioned strongly into LDW. I have therefore used it as a working principle that microdomains are 1-3 nm in thickness. Chaplin (Biophys.Chem 83: 211-221 1999) proposed that the microdomains in bulk water were 3 nm across.
Reviewer: How do the lock-and-key and induced fit models survive this model?
Wiggins: If reactions take place in solution then neither of these concepts is relevant.
Reviewer: Of all the enzymes that catalyze hydrolysis reactions, why are they not the same? Would one enzyme do for all?
Wiggins: Maybe they are essentially the same in this respect. Or there must be another level of specificity. Enzymes clearly differ from one another in the number and chemistry of their charged groups, positive and negative. These are very important sites of pockets HDW and LDW and it is probable that there is another level of specificity here. The pockets exist because of the osmotic pressure gradient set up by the counter-ion, rather than by the endogenous LDW/HDW equilibrium. They are better described, therefore, as pockets ‘enriched’ in HDW or ‘enriched” in LDW. The degree of enrichment depends upon many things including the chemistry of the counterion, the chemistry of the fixed charge, and the presence of other solutes which partition into either LDW or HDW.
I have no cut and dried answer here. We need more experiments.
Reviewer: What causes conformational changes in enzymes as they perform their catalysis?
Wiggins: To take a single example, when glucose ‘binds’ to hexokinase there is a large conformational change. Assuming that ‘binding’ of glucose means partitioning of glucose into a zone of LDW associated with hexokinase, we know that glucose produces more LDW (see Figure 2). If hexokinase is such a protein that it also produces LDW, then addition of glucose will increase ΔGw, so that the protein folds more tightly. If hexokinase partitions into LDW and produces more HDW, addition of glucose will decrease ΔGw and the protein will loosen up. Whichever applies, release of glucose allows hexokinase to revert to its original conformation. Thus conformational changes are manifestations of the operation of ΔGw.
Notice that one of the subtleties and sources of confusion of this scheme is that solutes, which produce more HDW in bulk water, produce more LDW in water at surfaces.
1 Professor of Molecular and Cell Biology, University of California, Davis.
