Unexpected Thermal Properties of Water Diffusion in Very Porous Materials

Unexpected Thermal Properties of Water Diffusion in Very Porous Materials

Signanini P1, De Santis A1,2,*, Di Fazio M3, Greco P1, Merla A1,4, Monosi S5, Piazza F6, Rainone ML1, Fenzi F7, Torrese P8

1Centro di Ricerche e Studi per le Geotecnologie, Università “G. d’Annunzio” di Chieti-Pescara, Campus Universitario, Chieti, Italy
2Istituto Nazionale di Geofisica e Vulcanologia, Sezione Roma 2, Roma, Italy
3Dipartimento di Ingegneria e Geologia, Università “G. d’Annunzio” di Chieti-Pescara, Campus Universitario, Chieti, Italy
4Dipartimento di Neuroscienze e Imaging, Università “G. d’Annunzio” di Chieti-Pescara, Campus Universitario, Chieti, Italy
5Dipartimento di Scienze e Ingegneria della Materia, dell’Ambiente ed Urbanistica, Università Politecnica delle Marche, Ancona, Italy
6Dipartimento di Ingegneria dell’Informazione, Università Politecnica delle Marche, Ancona, Italy
7Istituto di Chimica Inorganica e delle Superfici, Consiglio Nazionale delle Ricerche, Padova, Italy
8Dipartimento di Scienze della Terra e dell’Ambiente, Università di Pavia, Pavia, Italy

*Correspondence E-mail: angelo.desantis@ingv.it

Key Words: Water diffusion; Temperature; Capillarity; Porous material; Phase transition

Received March 22nd, 2014; Revised Oct 13th, 2014; Accepted Dec 1st, 2014; Published Dec 11th, 2014; Available online Oct 20th, 2015

doi: 10.14294/WATER.2014.6

 

Abstract

Significant and persistent decreases in temperature have been observed in very porous materials when they are partially immersed in water at room temperature. As the sample sizes were much smaller than the maximum height of the typical capillary rise, this represents a far-from-equilibrium system. We attribute this thermal decrease to two concurrent actions: (i) the highly porous property of the material used; and (ii) a transition-phase-like process of the water. Thus, the water not only cools down the material surface through evaporation at the sample–air interface, but it also expands within the material, causing a further internal decrease in temperature that cannot be explained solely through evaporation. This latter process is persistent enough to maintain the decrease in temperature over time. This unexpected characteristic of water and its persistence when diffusing inside an extremely porous medium are the most original results of this study. Our results seem in agreement with the recent model on the fourth phase of water by Pollack.

 

Article Outline

 

Introduction

Water is one of the most ubiquitous molecular compound on our planet. Water exists in all of its phases (gas, liquid and solid) and contributes to life, tectonics, atmospheric dynamics and many physical and chemical changes that occur on Earth1. Water has unique properties compared to other compounds, especially when considering other liquids, so that it can even be considered ‘eccentric’2. A remarkable thermal property of water is its very high heat capacity; i.e., the capacity to absorb a large amount of heat for every degree in temperature increase. Likewise the latent heat of water, both for melting and evaporation, is unusually high. In the process of evaporating, water draws heat from the air, thus cooling it.3

Another peculiar characteristic of water is related to capillarity4,5. This phenomenon appears when water fills narrow, thin channels in materials (i.e., capillaries): the water interaction with the channel walls produces a force that allows it to rise acting against gravity.

These properties represent the basis of the phenomenon we investigated here. We partly immersed a porous sample into de-ionized water and filmed the events both in the visible and infrared (IR) to detect any anomalies in the behaviour of the water (see Materials and Methods).

In the tradition of many countries, in the Mediterranean and Middle East regions in particular and in other hot climates6, some well-known schemes used to keep water cool and also of food, for example, in Italy, jars of Sicilian terracotta (earthenware) or a Tuscan glass flask covered with straw; in Spain, the popular Botijo, a clay jug; in Arab countries, a water bottle covered with a cloth, as well as the Arabian leather flask, an animal-skin container. These cooling systems are all characterised by a wet external surface, which takes advantage of either the water evaporation from the insulation or acts as a solar engine where the evaporating water at the surface produces a certain amount of refrigeration inside.

In this perspective, we know that if it is possible to cool by micronised water passing into a warm unsaturated environment, it is equally true that, if we put a container with water under the sun, as the water evaporates from the surface, it remains cool, while the water below the surface will warm up. Thus, in this system, the role of the water during evaporation, at first glance, would not appear as important as the characteristics of the container. It should also be noted that the common features of the above-mentioned traditional cooling systems that are based on water evaporation include a porous medium that is characterised by particular permeability, porosity, and pore sizes, such as to allow for capillarity action to take place.

Our experiments focused on the properties of the material such as terracotta, one of the most thermally efficient and most studied materials. Moreover, there is a rich bibliography on terracotta, which is one of the porous media of geological and geophysical interest7-13. Terracotta can also be defined in mineralogical, chemical and physical (mechanical) terms, and can be produced or modified by various parameters.14

The initial aim of our study was to determine whether the traditional cooling systems should be classified as insulators or as special heat engines. Once we recognised that these systems do indeed represent heat engines, we focused our attention on the diffusion of water in different kinds of porous materials, with special emphasis on the role of temperature during this process. What we describe and discuss here is an unexpected decrease in temperature due to an intriguing and not previously reported, property of water during diffusion.

 

Materials and Methods

The experiments were conducted in a room with controlled temperature (±1 °C), humidity and ventilation. In all of the experiments a small sample (e.g., a brick) was stood up on its end in a bath of demineralised water with a depth of 2 cm. The samples were of a size much smaller than the typical height of the capillarity rise; this means that the subjects of our experiments were basically far-from-equilibrium systems. All of the stages were recorded using at least an IR thermal camera (FLIR SC660 or SC3000) with high-quality thermal sensitivity (<30 mK and 20 mK, respectively, at 30 °C), to document the temperature evolution (Supplementary Information, Figure 1). Figures 1-4 show representative data from a selection of the most significant experiments at three stages: the initial (starting), intermediate (within ca. 10 minutes) and final (thermal equilibrium, as ca. 24 hour) stages.

For the porosity, we further analysed and compared both unmodified and modified bricks. Some porosity measurements have been performed at the Dipartimento di Scienza e Ingegneria della Materia, dell’Ambiente e Urbanistica (Università Politecnica delle Marche, Ancona) by using a WIN9400 series mercury porosimeter (Micromeritics Instruments Corporation). Some other porosity measurements have been performed using a helium pycnometer with ± 0.01% accuracy (AccuPyc II 1340, Micromeritics Company), installed at the HPHT laboratory of the Istituto Nazionale di Geofisica e Vulcanologia (Rome, Italy). Supplementary Information Figure 2 shows the data from the mercury porosimeter: the modified sample (Supplementary Information, Figure 2b, high-efficiency brick) had a greater porosity (of 60%) with respect to the unmodified commercial brick (Supplementary Information, Figure 2a, of 30%). Moreover, the porosity spectrum of the high-efficiency brick was much wider than the commercial brick, as it extended over almost three orders of magnitude. In this respect, we do not exclude that smaller pores are present in the commercial brick, as the limits of these measurements do not allow greater resolution. This is essentially shown by the results from the Helium picnometer, which confirmed the difference in porosity between the commercial and high-efficiency bricks (35% and 58%, respectively), and provided an even greater value of around 75% for another further modified sample. Another important result from the Helium picnometer is that the high-efficiency brick was composed mainly of interconnected pores, showing this aspect to a much greater extent than the commercial brick. It is also this characteristic of the pore configuration that allows the greater water diffusion within the high-efficiency bricks, as much greater than the commercial bricks.

 

Results

Water Capillarity in Commercial Bricks

We initially took several commercial bricks with different porosities and chemical-mineralogical characteristics, and we put them in small containers that were partially filled with water at room temperature, and then we created the appropriate conditions for capillary rise (Supplementary Information, Figure S1). A similar study was performed by Ricken15, although he did not consider the temperature variations of the system.

Our results show that:

  • during the capillary rise of the water in the brick, there is a decrease in temperature that is related to the degree of water saturation;
  • the temperature difference relative to its environment is maintained even when the brick becomes completely saturated;
  • a decrease in the temperature does not occur with bricks with painted or glazed surfaces where evaporation is suppressed;
  • there appears to be a relationship between the maximum height of the capillary rise and rate of rise and the amount of cooling;
  • the temperature variations of the brick are a function of both the chemical-mineralogical characteristics of the material and the physical parameters, such as porosity and surface properties.

Some of our experimental observations are supported by reports in the literature (e.g., water absorption and water transport by the bricks16-18), but others are not explainable on the basis of present knowledge (e.g., by capillary flow within the bricks5,19,20). This is probably because some reports regard organised systems, while others regard single elements. One example is that the largest cooling effect occurs in the most porous materials, while the opposite might be expected because the specific heat of water is much greater than that of terracotta.

The ‘High-Efficiency’ Brick

Starting from the above basic considerations we attempted to produce a brick that would be specifically suitable for our study. To assess the efficiency of the process we carried out a series of tests, such as x-ray diffractometric and chemical analyses of the materials.

In view of the mineralogical and petrographic complexity of natural clays, it was decided to choose a basic type of clay with optimal starting characteristics. Then we varied its physical parameters to produce the best bricks for our purposes. In particular we measured:

  • Total porosity
  • Capillary porosity
  • Porosity spectrum
  • Volumes, shapes and evaporating surfaces

At any modification of the above mentioned parameters on the prepared samples, we carried out porosimetric (Hg, He) analyses, estimated rate of capillary ascension, thermography and kinetic temperature measurements. All the measurements were undertaken at constant temperature and humidity, but at varying time t, velocity u, and height h, at different atmospheric pressures and rates of evaporation with respect to the surfaces of an equivalent volume of bulk H2O; and at different masses of saturated samples for capillary ascension and immersion.

We have also carried out:

  • Measurements of the internal pressure.
  • Tests of heat stress

The above actions were applied on different bricks which, derived from the afore-mentioned clays, were subjected to different firing aimed at obtaining bricks with the highest efficiency.

Whereas the characteristics of terracotta in terms of the capillarity are a function of both the mixture of the clay minerals and their transformation during firing, we used ceramic materials that were derived from natural clays (of one basic mineralogical type only) and were specifically designed and manufactured, and are characterised by:

  • porosities of around 60% (Supplementary Information, Figure S2);
  • good correlation between the water rise within the brick and the decrease in temperature (Supplementary Information, Figure S3)
  • nearly fully interconnected pores; – a ratio of >0.95 between saturation by capillarity and saturation by total immersion (after one week total immersion in water);
  • a porosity spectrum that showed a range of pore diameters, ranging from hundreds of microns to tens of nanometers.

Under the same macroscopic geometric characteristics and temperature–humidity conditions of testing, during the rise of the water capillary, ‘high efficiency bricks’ show larger temperature decreases than commercial bricks. Such high-efficiency bricks can also show a capillary rise of the order of metres (we demonstrated this result, extrapolating in height our experiments, that is also confirmed in building walls17), and during the initial phase of water diffusion, a speed of capillary rise from 0.1 mm/s to 1 mm/s (data not shown). Furthermore, we were also able to measure a small, but definite decrease in the internal pressure with respect to the atmospheric pressure inside the fully saturated samples (depression of 40-50 mbar; data not shown).

Water Up, Temperature Down

In the first experiment, a sample was immersed for the first few centimetres in water in a plastic cup. Figure 1a illustrates this experimental setting, with the different radiant temperatures measured through IR imaging, initially (Figure 1b), after ca. 10 min (Figure 1c), and 24 hours later (Figure 1d). As can be seen from the tabulated data, this water–brick system worked as a thermal engine, which decreased the temperature of the brick to 4.8 °C lower than the final environmental temperature (Figure 1d, Ar03 versus Ar01). We also noted a smaller decrease in the temperature of the water of the supply system (Figure 1).

Figure 1: Decreases in the temperature in bricks during water capillarity. a, Photograph of the set-up. b-d, Sequential IR photographs (see main text). Tables show the radiant temperatures measured in the indicated regions of the IR photographs.

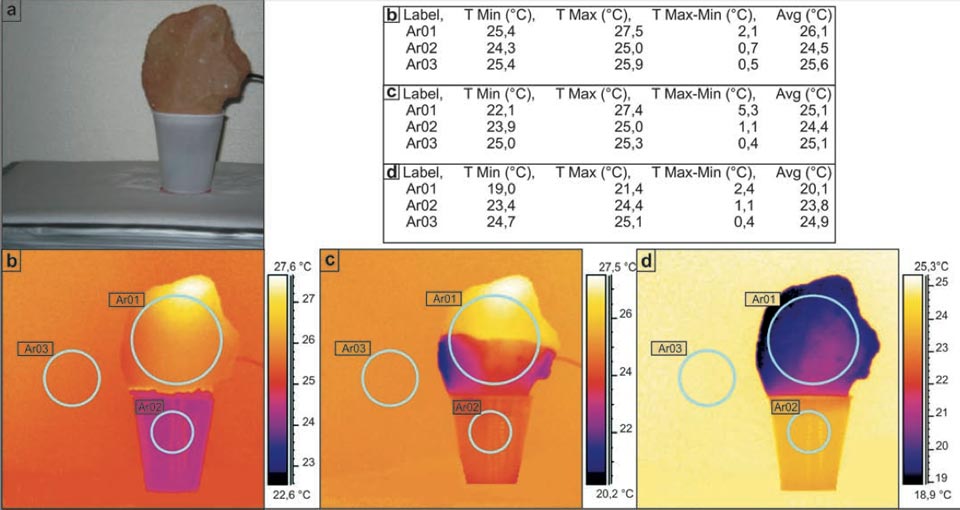
Figure 1: Decreases in the temperature in bricks during water capillarity. a, Photograph of the set-up. b-d, Sequential IR photographs (see main text). Tables show the radiant temperatures measured in the indicated regions of the IR photographs.

 

Influence of Sample Shape

The next experimental system investigated samples of different shapes (Figure 2; but see also Figure 3 for other shapes, e.g. the “hourglass”). The objective here was to investigate how the geometry of the samples might affect the water rise and the decrease in temperature achieved. In a dedicated laboratory with an ambient temperature of ca. 23.5 °C, all of the samples showed final temperatures of around 20 °C (Figure 2d, Ar01, Ar03, Ar05, Ar07: 20.1 °C, 20.0 °C, 20.5 °C, 19.9 °C, respectively), Here, the rhombic sample (Figure 2, Ar05) showed a slightly lower efficiency. The use of these different shapes indicated the clear character of the water diffusion within the samples. Where the geometry of the initial diffusion can be modelled with an apex (i.e., the rhombus and T-shaped bricks; Figure 2c, Ar05, Ar06), the process acts as a point diffusion. Please note that the slightly different color of the background in Figure 2b-d is mainly due to the different scale ranges of the palette.

 

Figure 2: Influence of sample shape on the decreases in the temperature in bricks during water capillarity. a, Photograph of the set-up. b-d, Sequential IR photographs (see main text). Tables show the radiant temperatures measured in the indicated regions of the IR photographs.

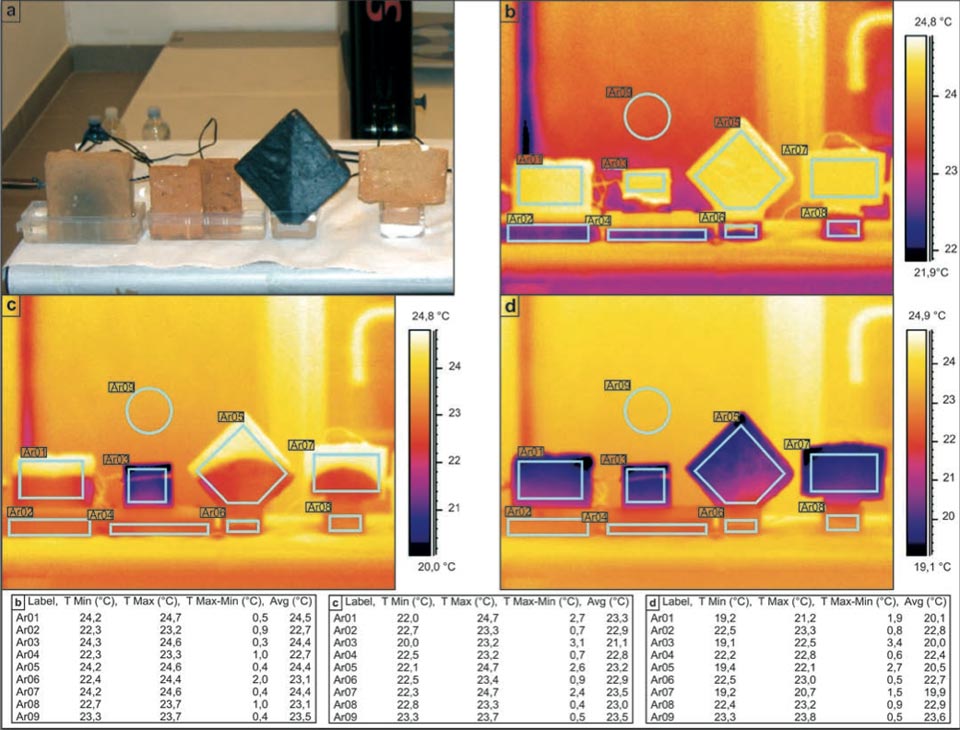
Figure 2: Influence of sample shape on the decreases in the temperature in bricks during water capillarity. a, Photograph of the set-up. b-d, Sequential IR photographs (see main text). Tables show the radiant temperatures measured in the indicated regions of the IR photographs.

 

Influence of Evaporation Surface

Although the area of the evaporation surface of a porous medium is not a parameter that can be easily defined, as it is likely to be fractal21,22,23,24, different experimental systems were designed to determine the relationship between the evaporation surface and the degree of cooling. Here, a unique brick shape was used, whereby the original bricks could be cut into two equal parts (Figure 3a-d). The system was thus investigated with the two parts kept in contact or split. In both the cases, although with different surface of evaporation, we obtained the same temperature decreases (Figure 3c, Ar01, Ar03: 18.1 °C versus 20.4 °C; Figure 3d, Ar01/Ar02, Ar04: 18.4 °C/18.5 °C versus 21.4 °C). These data show that although evaporation is important, it does not have a crucial role.

 

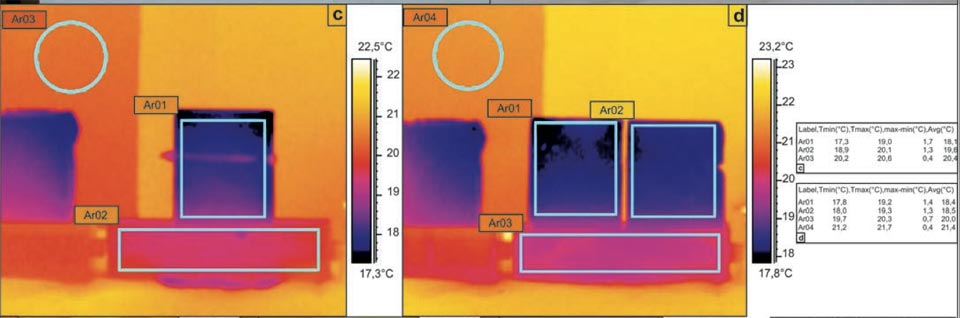
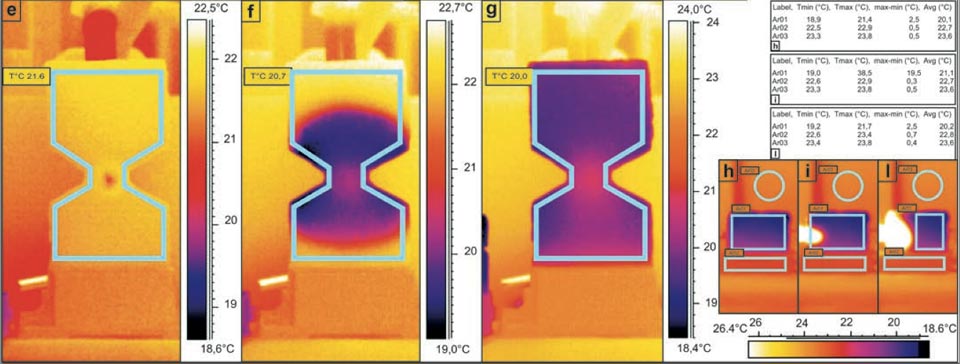
Figure 3: Water capillarity in high-efficiency bricks. a, b, Photographs of the set-up. c-l, IR photographs (see main text). Tables show the radiant temperatures measured in the indicated regions of the IR photographs. c, d, Diffusion in a sample cut in two parts: in contact (c), and separated (d). e-g, Water added to the centre of the hourglass shaped brick (see main text). h-l, Thermal effect due to the contact of an electric soldering iron with 50 W of power on the left side of the brick (see main text).
Figure 3: Water capillarity in high-efficiency bricks. a, b, Photographs of the set-up. c-l, IR photographs (see main text). Tables show the radiant temperatures measured in the indicated regions of the IR photographs. c, d, Diffusion in a sample cut in two parts: in contact (c), and separated (d). e-g, Water added to the centre of the hourglass shaped brick (see main text). h-l, Thermal effect due to the contact of an electric soldering iron with 50 W of power on the left side of the brick (see main text).
Figure 3: Water capillarity in high-efficiency bricks. a, b, Photographs of the set-up. c-l, IR photographs (see main text). Tables show the radiant temperatures measured in the indicated regions of the IR photographs. c, d, Diffusion in a sample cut in two parts: in contact (c), and separated (d). e-g, Water added to the centre of the hourglass shaped brick (see main text). h-l, Thermal effect due to the contact of an electric soldering iron with 50 W of power on the left side of the brick (see main text).

Figure 3: Water capillarity in high-efficiency bricks. a, b, Photographs of the set-up. c-l, IR photographs (see main text). Tables show the radiant temperatures measured in the indicated regions of the IR photographs. c, d, Diffusion in a sample cut in two parts: in contact (c), and separated (d). e-g, Water added to the centre of the hourglass shaped brick (see main text). h-l, Thermal effect due to the contact of an electric soldering iron with 50 W of power on the left side of the brick (see main text).

The amount of water that evaporated from the ‘high-efficiency’ brick was ca. 1.5-fold that which evaporated from the container filled with water with an evaporation surface equal to that of the sample, under the same conditions, over 24 hours. We also found that the colder thermal state persists also if severe thermal stress conditions (such as for instance a persistent external heating of the brick) have applied at the sample surface (Figure 3 h-l).

 

Influence of Gravity: the ‘Hourglass’ Brick

When the water was applied continuously (by gravity from a container placed above through a small pipe) at the centre of a hourglasss brick sample (Figure 3a, b, e-g), it showed clear quasi-symmetric diffusion, with an almost spherical spreading from the point of application through the rest of the sample. This thus demonstrated the almost identical characteristics of the diffusion in both the upward and downward directions. (Please note, indeed it seems that the downward diffusion is a little more impeded than upward diffusion; we will discuss this particularity below).

Here there was also a final temperature decrease of 3.3 °C with respect to the room temperature (Figure 3g, 20.0 °C versus 23.3 °C).

This experimental system showed that gravity has negligible influence on the capillarity of the water in these bricks16. A further significant aspect here was the presence of a slightly lower temperature at the diffusion front with respect to the innermost portion of the system (Figure 3f). The same results were obtained when this hourglass brick was rotated by 180° with the water applied only once as a drop. The gas-like behaviour of the water inside the sample

The analogous situation of low-pressure butane gas injected into the centre of the hourglass brick sample was then investigated (Figure 4). This system was designed to show the strong analogy between the water in the previous system (with the hourglass brick sample) and the use of a gas instead of water. Figure 4 shows this system both 91 s (Figure 4a) and 360 s (Figure 4b) after the injection of the butane gas at the centre of the hourglass brick sample.

 

Figure 4: Butane gas injection into the centre of the hourglass shaped brick (see main text).

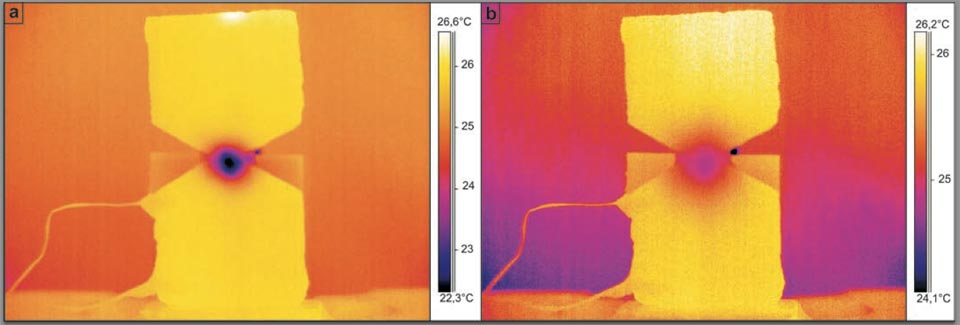
Figure 4: Butane gas injection into the centre of the hourglass shaped brick (see main text).

 

This overpressure injection also cooled the centre of the hourglass brick sample by ca. 4 °C. This is similar to what happens when the water enters the porous brick samples (though the gas effect was expected to be generally colder, it was not.

The Temperature Inside the Brick

Here, we also measured the temperatures inside the samples, with the insertion of several high-sensitivity digital thermometers from bottom, into holes containing the internally diffused water (Supplementary Information, Figure S5). The most ‘efficient’ brick system was used in this case: a cylindrical shape to provide the highest porosity possible, with the most rapid water rise and highest cooling efficiency, i.e. lowest temperature achieved. This aspect was important for understanding the extent of the role of evaporation in this process.

To provide minimum differences between the kinetic and radiant temperatures on the sample surface without changing the rate of water evaporation, these samples were also fully covered with a black Cu silicate paint. The system was then run for 24 hours, after which, the temperature within the sample reached ca. 16 °C, i.e., 7 °C lower than the room temperature of 24 °C (Supplementary Information, Figure S4b; the temperature inside the sample at the end of the experiment is given in Kelvin). This result is important, because it confirms that, although evaporation is one of the components involved in this process, there is something else that produces an decrease in temperature, and this “something” occurs inside the porous solid because of the presence of water.

 

Discussion and Conclusions

The results presented here and illustrated by the preceding figures raise doubts as to whether or not the observed phenomena can be explained or understood within the framework of classical models that are primarily based on the capillarity of the samples.

Let us suppose that, as suggested by our experiments, the phenomenology is unique and that hydrophilicity of the material, capillarity, rising and cooling of the water are all parts of a complex thermo-electro-dynamic process. Thus we need to analyze with this perspective in mind the experiments reported here. We will attempt to give an overall explanation based on the capillarity process, the subsequent cooling and inferred saturation of the samples, and the dynamic equilibrium that maintains the sample stably at a lower temperature relative to the external environment.

To explain the different features, we will take into consideration a recent unifying model25, that proposes a fourth phase of the water. We recognize that, according to this model, we can explain the different peculiar aspects that emerged from our experiments.

In hydrophilic materials, namely those that have great affinity with water, there is the phenomenon of capillary rise because these materials are able to change the water dissociation constant K :

K = [H+] * [OH–]/[H2O]

This ability to dissociate the water is present at the contacts between layers of the same material (e.g. Nafion®) or inside the material (e.g. terracotta ) where, consequently, it is possible to create a type of water dipole. So, according to Pollack’s model25, we will call the non-dissociated water as H2On (n stands for “normal water”), the negatively charged as H2Oez (ez stands for “exclusion zone”), the other, positively charged, as H2Op (protonated water).

From the literature we know that the process of water polarization (i.e. the orientation of the water molecules taken as electric dipoles) requires energy that can be in the visible light (0.5-0.9μm wavelength) and in the near infrared (3 – 5μm), but as shown by our experiment on an almost black body sample (emissivity ε ≈ 1; Figure S4a), measuring the kinetic temperature and the radiant temperature with a bolometric IF-camera (frequency range 7-14 νm; Supplementary Information, Figure S1) gives nearly the same results. So we can state that the electric field can be fed by the environmental heat (of the medium) and that it, consequently, contributes to the cooling of the sample. This is what is expected by the fourth phase of water model25 in the passage from H2On to H2Oezz + H2Op, when conditioned by certain parameters, one of which is the degree of affinity between water and the material (in our case the terracotta; in the case described by Pollack25, the material was the Nafion), which is related to the maximum potential difference ΔVmax occurring in the “exclusion zone” ez.

If we assume the same mechanism25 and consider the experimental situations, we must take into account that, in the case of the Nafion, the degree of affinity towards water seems to be higher than in the case of our bricks (hence the ΔVmax betweenH2Oez and H2Op in the Nafion is greater than in our case). On the other hand, in our case, we are dealing with a system with a much higher surface area. For example, our sample has a volume of 250 cm3 so that for a capillary porosity of around 65-70% and an average pore diameter of around 50-100μm, the active surface is of the order of some hundreds of m2.

Therefore we have to consider the affinity function of ΔV and of the surface as a function of the quantity of electrons, Qe, consequently, of the current I. Thus, let us assume that the same mechanism occurring in the batteries with Nafion25 also occurs in our terracotta system. If the work in the former case is ΔV*I, in our case the work of the electric field, which manifests itself by raising the water mass up to a certain height and by cooling the medium, will provide the energy necessary to run the said process.

A mechanism of this type may also explain why, at the level of the single capillaries, the smaller the diameter the higher the raise of the water. Thus, we can establish the equivalence: equal electric field means equal amount of cooling, which, in turn, means equal work. This, of course, happens for situations of a single capillary. For situations of multi-capillarity, the problem is more complex, but we can see, analyzing the individual experiments performed (Supplementary Information, Figure S3) as initially the raise of the water is fast, and then slows down as the amount of work performed by the electric field results in a nearly constant “far-from-equilibrium” situation, which is typical for many complex systems22.

Regarding the detailed mechanism and the relative formation of H2Oez + H2Op in the process of interaction between water and the hydrophilic material, both Figure 2 and Figure 4 are informative because the diffusion in these media is similar to that of a gas. This further supports Pollack’s hypothesis about the nature of H2Op and its organization, mobility, and, in our opinion, also its lightness, i.e. a lower density. Indeed, by more closely observing Figure 3 (the hourglass case), it will be noted that the downwards movement of the water seems impeded, even though gravity should favor it: this would confirm the lower density of this kind (H2Op) of water.

On the other hand, the pressure measurement made within the sample of Figure S4a, showing a depression of 250 mmHg, could be explained by the mechanism proposed by Pollack’s model25: as the density of the water, in its transformation into H2Oez, decreases, the reorganized H2Op will occupy more space: this kind of water will divide into droplets, eventually creating bubbles, and hence will cause a general decrease of pressure. On the other hand, it is possible that in some way the H2Oez layer that forms along the interface of the medium at the air-water contact, allows this phenomenon to take place. So we could explain the observed depression (i.e. the lower inner pressure) by the increased speed,, with which the water is supplied from the container to the medium, especially when subjected to heat stress conditions.

As to the effect of temperature on the capillary rise, and consequently on the degree of cooling of the sample, our experiments have always demonstrated (at least in the temperature range from 10°C to 50° C) a direct proportionality between room temperature and ΔΤ, compared to that measured both inside and outside of the various samples. This is in agreement with what expected by Pollack’s model25, because any increase in the ambient temperature, and therefore a greater amount of energy available, will cause an increase of the exclusion zone, consequently an increase in the capillary hmax and, then, as stated above, in a higher rate of cooling. Looking at the experimental results in the light of Pollack’s model25, we are led to analyze in detail a series of experiments that did not coincide with what is expected on the basis of classical physics. For example, if the brick under study were made of a set of smaller capillaries, it would have raised the water (maximum capillary height), would have increased the speed of capillary ascension, and would have caused an even more pronounced cooling (we always have to keep in mind that our experiment corresponds to far-from-equilibrium conditions).

Actually, the best performance in terms of cooling was found for those samples for which the capillarity spectrum was more evenly distributed and in which the interconnectivity between pores was highest. We think that the solution to this problem is as follows. Let us consider a small capillary size whose diameter φ is less than 1 μm (i.e. φ <1 μm) and characterized by a height much larger than φ. This fact would in principle predict a very high rise, but, if we analyze the same situation with the rising model proposed by Pollack25, it seems clear that there will be a limit given by the condition that, if the potential difference ΔV, between H2Oez and H2Op, reaches its maximum value, ΔVmax, allowed by the water affinity and medium, then the dissociation constant reaches its maximum value Kmax. Therefore it is clear that, once the differential potential reaches its maximum value ΔVmax, the type H2Op of water cannot further dissociate, therefore implying that there is a limit to the capillary rising. This could be a simple explanation why the best cooling was obtained in samples with broader porosity spectra and with more intercommunicating capillaries: while the smaller capillaries will develop a greater surface area (with respect to their section) and, in turn, a higher electric field, the larger intercommunicating capillaries will allow water to better feed these capillaries by making a kind of water that is less dissociated.

Let us keep in mind that, although there are different models of capillary rise -capillary rate in the literature16,19,20, we believe in the validity of a particular innovative model25, at least with respect to our main goal, maximum cooling, which means that the amount of power generated by the material during the process is of interest.

Having thus understood capillary diffusion and cooling, i.e. the dynamics of the generation of lower temperatures, the second important issue is: why does this cooling persist?

It would have been more logical that, once the energy was used for the work of lifting a given mass of water to the limit h* of the maximum capillary ascension (or of the sample size), the cooler part of the material would tend to heat up so as to be in balance with the environment. It would thus be expected that the remaining work will be used to solely maintain the electric field, which requires a much smaller amount of energy.

The same problem can be seen in a totally different way; we can ask ourselves: where will the heat energy go (i.e. the energy that the external system transfers to the brick but does not put the latter into temperature equilibrium with the environment)? To solve this problem we made a series of thermal stress tests which provided additional interesting information, especially regarding the behavior of systems at constant room temperature.

To understand the above problem, among various possible approaches, a simple experiment was optimally conclusive. In this experiment we considered a serial electric circuit, formed by our sample, a 10 Ω resistance, and a voltage DC supply. We then applied a voltage such that the temperature of the same increases, by Joule heating, to maintain the same initial ambient temperature, e.g. 5 ° C above the temperature of the sample without additional heating.

The experiment has lasted for more than 14 hours. Neglecting that there was a slight temperature drop in the cooling water supply (about 0.5° C) and a slight temperature drop of ventilation air (about 0.1° C), at the exit with respect to the input, if we compare the data of water consumption with the consumed watts, the result was astonishing: to keep the sample at the same ambient temperature required about 10W! This provides an estimate of the power involved in the cooling of our thermodynamic system.

It would seem that the wasted heat compared to the latent heat of the consumed water is around 90%. It is clear that in addition to the possible practical implications, the result is puzzling because it would seem that around 85% of the energy of the water passage from liquid state to vapor state, is spent for the passage from H2On to H2Oez + H2Op and only a remaining 10% is spent for the transition from the liquid polarized water to vapor. This is a remarkable fact in as much as it confirms the hypothesis that the gaseous state of air (oxygen-nitrogen) and water vapor are not simple molecular systems but are actually highly organized and complex structures. If this were not so, it would be hard to understand why more than 85% energy serves to switch the system to an ordered structure while the remaining 15% is passed to a completely different structure, which in any case should be given for requiring a very different energy supply.

So, given the experimental results reported here, we think that, from an energy point of view, the fourth phase of water should be placed between H2On and gaseous, and, more correctly, in a state with properties much closer to the gas phase than the classical liquid phase.

 

Acknowledgements

We thank Silvio Mollo (Istituto Nazionale di Geofisica e Vulcanologia) for his laboratory analyses on the samples. We also thank the personnel of Chieti-Pescara University who were involved in some of the experiments. Some of this work was undertaken by ADS under the project SAGA-4-EPR, co-funded by the Italian Foreign Office and Shenyang North-Eastern University (China) and the Istituto Nazionale di Geofisica e Vulcanologia.

 

Author Contributions

P.S. suggested and conceived this study. The authors contributed collectively to the design of the experiments. P.S., M.D.F., P.G. made the terracotta samples. A.M. set up the IR equipment. P.S., A.D.S., M.D.F., P.G., A.M., M.L.R., F.F., P.T. performed IR experiments. S.M. carried out the porosity analyses. A.D.S and F.P. contributed to the discussion of energy balance and efficiency involved in the processes. P.S. and A.D.S. wrote the first draft of the manuscript, and then all of the authors contributed equally to improve the manuscript.

 

Competing Financial Interests

P.S. is the proprietor of the Italian patent – application No. BO2011A 000337 dated 10 June 2011 – “Metodo per la conversione di energia e convertitore di energia” and International patent – application No. PCT/IB2012/052949, dated 11 June 2012 – “Method for the conversion of energy and energy converter”.

 

Supplementary Information

 

Figure S1: General setting and IR recording of the experimental system.

Figure S1: General setting and IR recording of the experimental system.

 

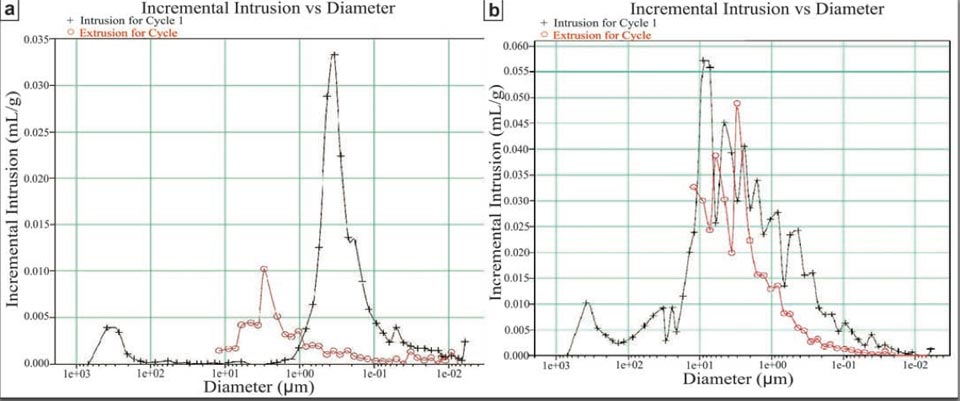
Figure S2: a, commercial brick, showing a porosity of around 30%. b, High-efficiency brick, showing a porosity of around 60%. Both of these spectra were obtained using a mercury porosimeter.

Figure S2: a, commercial brick, showing a porosity of around 30%. b, High-efficiency brick, showing a porosity of around 60%. Both of these spectra were obtained using a mercury porosimeter.

 

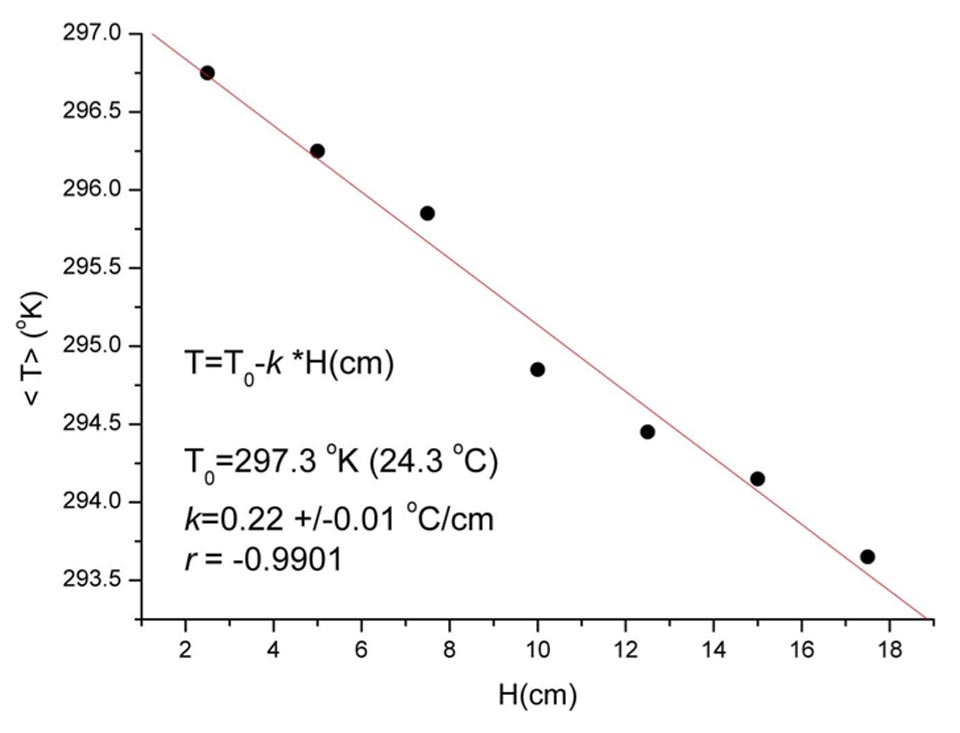
Figure S3: Temperature versus water height capillarity correlation of high-efficiency bricks.Decreases in the temperature T with the water rise H in the high-efficiency bricks (20 cm high). This is not due to the conservation of energy, as when the kinetic energy (proportional to T) decreases, the potential energy (proportional to H) increases.

Figure S3: Temperature versus water height capillarity correlation of high-efficiency bricks.Decreases in the temperature T with the water rise H in the high-efficiency bricks (20 cm high). This is not due to the conservation of energy, as when the kinetic energy (proportional to T) decreases, the potential energy (proportional to H) increases.

 

Figure S4: Temperature measurements within a high-efficiency brick cylinder during capillarity. a, Cylindrical brick with holes to insert the high-sensitivity thermo-sensors. b, Temperatures recorded inside the cylindrical sample during a capillarity experiment. The central hole (at ca. 3 cm from each side) reaches the lowest temperature. This cannot be explained simply by evaporation.

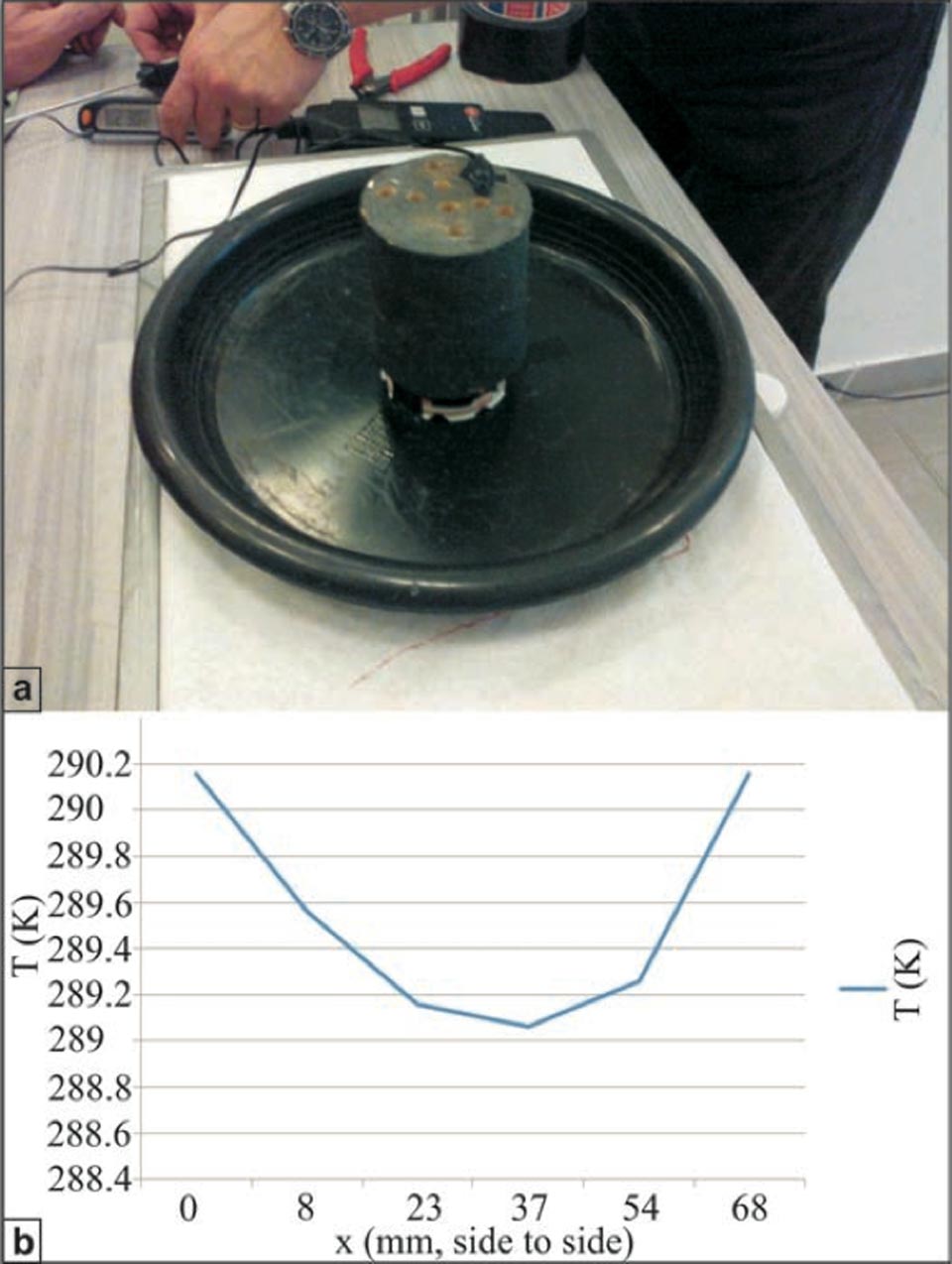
Figure S4: Temperature measurements within a high-efficiency brick cylinder during capillarity. a, Cylindrical brick with holes to insert the high-sensitivity thermo-sensors. b, Temperatures recorded inside the cylindrical sample during a capillarity experiment. The central hole (at ca. 3 cm from each side) reaches the lowest temperature. This cannot be explained simply by evaporation.

 

References

1. Lerner KL, Lerner BW (Editors) (2005). UXL Encyclopedia of Water Science. Thomson Gale, USA.

2. Franks F (2000). Water: a Matrix of Life. 2nd edition. RSC Paperbacks, Cambridge.

3. Riley C (2006). The Unique and Unusual Properties of Water. Hyro Service and Supplies, Inc.

4. Roura P (2005). Thermodynamic derivations of the mechanical equilibrium conditions for fluid surfaces: Young’s and Laplace’s equations. Am J Phys 73: 1139-1147.

5. Roura P (2007). Contact angle in thick capillaries: a derivation based on energy balance. Eur J Phys 28: L27-L32.

6. Evans L (2004). The Advent of Mechanical Refrigeration Alters Daily Life and National Economies Throughout the World. Science and Its Times. Gale Group.

7. Biot MA (1941). General theory of three-dimensional consolidation. J Appl Phys 2: 155-164.

8. Bashad I (1952). Part II: properties of clays. Adsorptive and swelling properties of Clay-Water System. Clay Clay Minerals 1, 70-77.

9. Grim RE (1962). Applied Clay Mineralogy. McGraw-Hill Book Co, New York 36, pp 422.

10. Mitchell JK, Soga K (1976). Fundamentals of Soil Behaviour. 3rd ed. Wiley, New Jersey,

11. Winkler K, Nur A (1979). Pore fluids and seismic attenuation in rocks. Geophys Res Lett 6: 1-4.

12. Delville A (1993). Structure and properties of confined liquids: a molecular model of the clay-water interface. J Phys Chem 97: 9703-9712.

13. Domenico PA, Schwartz FW (2000). Physical and Chemical Hydrogeology. John Willey and Sons, New York.

14. King AG, (2002). Ceramic Technology and Processing. William Andrew Publishing, New York.

15. Ricken T (2003). Transport of fluids in capillary porous solids. Proc Appl Math Mech 2: 384-385.

16. Hall C, Hoff WD (2002). Water Transport in Brick, Stone and Concrete. Taylor & Francis, London, UK and New York, NY.

17. Massari G, Massari I (1993). Damp Buildings, Old and New. Rome, Italy: ICCROM. (English translation of “Risanamento Igienico dei Locali Umidi”) Milan, Italy: Ulrico Hoepli (1985).

18. Raimondo M, Dondi M, Gardini D, Guarini G, Mazzanti F (2009). Predicting the initial rate of water absorption in clay bricks. Constr Build Mater 23: 2623-2630.

19. Xiao Y, Yang F, Pitchumani R (2006). A generalized analysis of capillary flows in channels. J Colloid Interf Sci 298: 880-888.

20. Young WB (2004). Analysis of capillary flows in non-uniform cross-sectional capillaries. Coll. Surf. A: Physicochem Eng Aspects 234: 123-128.

21. Mandelbrot B (1977). Fractals: Form, Chance and Dimension. W H Freeman and Co.

22. De Santis A (2009). Geosystemics, Proceedings of the 3rd IASME/WSEAS International Conference on Geology and Seismology (GES’09), Cambridge.

23. Deinert MR, Parlange JY, Cady KB (2005). Simplified thermodynamic model for equilibrium pressure in a fractal porous medium. Phys Rev E 72: 0412032005.

24. Turcotte D (1997). Fractals and Chaos in Geology and Geophysics. 2nd Ed., Cambridge University Press.

25. Pollack GH (2013). The Fourth Phase of Water. Ebner & Sons Publishers, Seattle, Washington.

Close Menu