 Plasma-like Behaviour of Partially-Ionized Liquids Part I – The Floating Water Bridge
Plasma-like Behaviour of Partially-Ionized Liquids Part I – The Floating Water Bridge
Johnson R J1*
1Independent researcher, Oxford, UK
*Correspondence: E-mail: bob.johnson1000@gmail.com
Key Words: Plasma, Ionized Gas, Floating Water Bridge, Partially-ionized Liquid
Received January 23rd, 2012; Accepted March 13th, 2012; Published April 28th, 2012; Available online May 20th, 2012
Summary
It is suggested that charged particles in partially-ionized liquids are subject to similar forces as their counterparts in ionized-gas plasma and that an analysis of these forces can offer an explanation for the anomalous behavior of various partially-ionized liquids. In this paper, the behavior of the Floating Water Bridge (FWB) is compared to the filamentary behavior of Birkeland Currents in ionized-gas plasma. Plasma theory applied to the ions in the water of the FWB provides additional insights into aspects of the behavior of the FWB which are as yet imperfectly explained by other analyses. The correspondence between the behavior of the FWB and Birkeland Currents suggests that the application of plasma principles to partially-ionized liquids is valid and therefore may have wider applications in biological situations also involving partially-ionized liquids.
Article Outline
- Introduction
- The Floating Water Bridge
- Summary of the Characteristics of the Stable Stage of the FWB
- Existing Analyses of the FWB
- The Behavior of a Plasma Birkeland Current
- Comparison of the Characteristics of a Birkeland Current (BC) in Plasma and the FWB
- Discussion of the Stable Form of the FWB with reference to BC Dynamics
- Discussion
- Conclusions and Future Research
- References
- Discussion with Reviewers
Introduction
The anomalies in the behavior of water are well known and have inspired a large amount of research designed to develop a full picture of water behavior. Nevertheless, water is still not fully understood. Fuchs recently summed up the position:
“Much work has been done recently toward the simulation of liquid water, its intrinsic ions H+ and OH– and other ions in solution using ab initio electronic-structure methods, sometimes together with quantum dynamics methods, but still more work is called for in order to get a more complete and accurate picture of the liquid”. [Fuchs, 2010, p382]
At the same time, much research has also been carried out into the behavior of plasma in the form of an ionized gas, although this work is usually carried out by entirely separate groups to those studying the behavior of water.
The behavior of ionized gas plasma depends on the interaction of electric and magnetic fields with the individual charged particles in the plasma.
This paper suggests that, in principle, the charged particles in a partially-ionized liquid will be subject to similar interactions with electromagnetic fields as the charged particles in an ionized gas plasma, although these interactions will be modified by the liquid state of the medium.
Nevertheless, a comparison of plasma behavior and some anomalous behavioral characteristics of water indicates that further insights into the latter may be gained by applying the principles of plasma behavior to partially-ionized liquids.
In Part I of this paper, a comparison is made between the Floating Water Bridge (FWB) and Birkeland Currents in plasma. Future parts of the paper already in preparation will explore the application of these principles to biological situations involving plant sap flow and mammalian blood flow.
In recent years, a considerable amount of research has been directed into the newly re discovered phenomenon known as the Floating Water Bridge.
When a potential difference is applied between two beakers of pure water a small distance apart, a bridge of water forms between the beakers and remains stable while the potential difference is maintained. The beakers can even be separated by up to around 25mm without the bridge collapsing under its own weight or surface tension effects.
It is clear that the phenomenon depends on the applied electric field. What is not yet fully explained, despite the many investigations into the phenomenon, is exactly how the water interacts with the electric field.
This unusual behavior of the FWB has prompted some observers to observe that “The interaction of water with electric or magnetic fields also reveals many interesting aspects. The effect of magnetic fields seems extraordinary.” [Fuchs, 2010, p383] and “…considering water as an electric ferrofluid subject to high electric fields allows for structures that are more than just a bit unusual…” [Widom et al, 2009, p6]
Existing analyses of the phenomenon can model many individual aspects of this unusual behavior in a FWB but no one theory can yet explain all the observations.
As Fuchs concluded in 2010: “However, [the FWB’s] final stage—a macroscopic, rotating cylinder with special optical properties through which two water currents run—still represents an interesting opportunity to further study and learn about the interactions of water with electric fields.” [Fuchs, 2010, p400]
It is principally these aspects of the FWB which remain to be fully explained by existing analyses.
Summary of the Characteristics of the Stable Stage of the FWB
The relevant known characteristics of the stable stage of the FWB can be summarized for present purposes as follows:
1. The FWB is a stable nearly cylindrical tube of water of 1-2 mm diameter extending up to 25mm between two beakers of pure water under the influence of a large (15 – 25 kV) applied electric potential difference [Fuchs et al, 2008, p2]
2. The FWB exhibits only very slight catenary bowing under the gravitational force, indicative of enhanced stiffness of the FWB and/or significant tension in the bridge preventing further sagging. The sag remains approximately constant as the filament diameter increases. [Fuchs et al, 2008, p2]
3. Two water currents run through the FWB in opposite directions. [Fuchs, 2010, p4]
4. The FWB has an inner core which is distinct from an outer annular layer. [Fuchs et al, 2008, p3]
5. Charge transport occurs across the bridge; the anode beaker acquires a larger net +ve charge. [Fuchs, 2010, p399 & Fig. 16]
6. Equality of final water flows in the forward and backward directions is established; this prevents the cathodic beaker overflowing despite initial net inflow during the early development stages of the bridge [Fuchs, 2010, p397]
7. The outer annulus rotates very fast (0.1 – 0.3 m/s [Fuchs et al, 2007, p3]) The rotation is clockwise when viewed towards the cathode [Fuchs, 2010, p396]
8. There is apparent (but unconfirmed) concentration of positive charge in the outer rotating layer and negative charge in the inner core. [Fuchs, 2010, p395]
9. The water rheology is similar to a ferrofluid; coherent domains are aligned under the influence of the applied electric field [Widom et al, 2009, p6]
10. The molecules in the rotating outer shell are polarised under the influence of the electric field. [Fuchs, 2010, p396]
11. Rupturing of the FWB tends to be explosive, in the nature of a whiplash, due to the release of constraining forces. [Fuchs et al, 2008, p4]
Researchers have approached the analysis of the FWB from both the classical electrohydrodynamic (EHD) and quantum electrodynamic (QED) directions.
The classical approach has wide-ranging industrial applications in electro-wetting and electrophoresis techniques where the behavior of the fluids is well understood in EHD terms. However, when applied to the FWB, there appear to be some anomalies with this approach.
The original classical electrohydrodynamic equations for a leaky dielectric cylinder under an axial electric field were published by Melcher and Taylor in 1969. The essence of the Taylor-Melcher model is that a small amount of free charge at the surface is enough to set the liquid into motion [axially] with velocities up to a few mm/s [Marin & Lohseb, 2010, p8] Also, electrodynamic currents are assumed to be so small that magnetic induction effects can be ignored. [Melcher & Taylor, 1969, p111]
The model was completed in 1997 by Saville, who postulated a stability condition for fluid cylinders subject to high axial electric field strengths. [Saville, 1997]
Burcham and Saville [2002] extended the earlier work and applied the Taylor-Melcher theory to a vertical liquid bridge suspended in a dielectric gas. Their conclusions were that the model needed an arbitrarily adjustable additional parameter in order to make the theory agree with experimental results. The authors state: “… although the quantitative agreement between theory and experiment for the cylinder–amphora transition is not as close as one might like, using surface transport as an adjustable parameter brings theory and experiment into agreement. However, this entails introducing a property that was not measured in the experimental study. Indeed, it is not clear how this measurement should be made. Nevertheless, the theory shows that bridge stability is acutely sensitive to surface transport.” [Burcham & Saville, 2002, p181]
Surface transport depends on surface conductivity. The authors had previously speculated as to the possible causes of variation in this parameter: “While one expects the surface conductivities at the two aspect ratios to be closer to one another, it should be noted that only small amounts of electrolyte are needed to produce conductivities of this magnitude. Contamination may also be a factor. Another possibility is that the density of ions in the surface is field dependent.” [Burcham & Saville, 2002, p180]
The same authors had studied bridges in low-gravity situations in 1999. The results had not been entirely as expected. They concluded that report: “Several observations conflict with what is expected with leaky dielectric liquids” including “Unexpected differences between the behavior of liquids with different conductivities…. At present we have no ready explanation for this behavior.” [Burcham & Saville, 2002, pp 54-55]
Widom et al. analyzed the water bridge tension terms of the Maxwell pressure tensor in a dielectric fluid. [Fuchs, 2010, p 388] They concluded that “The resulting tension in the water bridge sustains a siphon between two beakers” and which, they conclude, behaves as a Bernoulli flow between the two beakers, oscillating at around 5Hz. [Widom et al, 2009, p6]
Widom et al’s analysis assumed de-ionized water throughout. They state: “The need for de-ionized water in the experiment is evidently [required for] prohibiting conductivity effects from masking the insulating dielectric effects.” [Widom et al, 2009, p.016301-1]
However, the presence of charge in the beakers after a FWB experiment suggests that Widom’s analysis is incomplete despite its apparently ‘satisfactory’ agreement with observed catenary sagging. In fact, the observed conductivity effects would apparently mask the dielectric effects and so cast doubt on Widom’s analysis.
These and other observations may have prompted Del Giudice et al [2010] to suggest in 2010 that the EHD approach has limitations: “… present [EHD] theories have difficulties explaining more than a few of [water’s] properties at once, and no theory so far could satisfyingly explain one lately rediscovered phenomenon, the floating water bridge.” [Del Giudice, Fuchs & Vitiello, 2010 p9]
They argue instead that “The QED approach to this phenomenon provides a possible theoretical background for many of the bridge’s features” [Del Giudice, Fuchs & Vitiello, 2010, p9]
Fuchs [2010] summarized the early quantum approaches as follows: “From a quantum mechanical point of view, density functional theory indicates that an electric field would stretch the intermolecular hydrogen bonds in the water network, eventually breaking the three dimensional morphologies to form linear, branched, or netlike structures, resulting in dipolar water monomers aligning along the field axis which coincides with the water bridge axis.” [Fuchs, 2010, p 388/9]
Rai et al describe the molecular mechanism: “Summarizing the structural evolution [of chains from clusters], one may view the effects as if the applied field smoothens out the 3D morphologies of water clusters to form a linear, branched, or netlike structure by reorienting the water molecules along the field lines.” [Rai et al, 2008 p8]
But Fuchs offers a caution: “However, the calculated field strength necessary in order to achieve such chains could are considerably higher than the ones applied in the water bridge experiment.” [Fuchs, 2010, p388/9]
Fuchs goes on to suggest that quantum field theory (QFT) can explain many features of the water bridge. In particular, QM coupling can form coherent domains in water in which all the molecules oscillate in phase. Application of an external electric field tends to align these coherent domains to form super-domains, thereby leading to Widom’s analogy of water as an “electric ferrofluid”. [Fuchs, 2010, pp 389- 390]
Fuchs summarizes: “When addressing the properties of the water bridge, QFT can predict many of its features, such as … the stability of the bridge due to the formation of super-domains …” [Fuchs, 2010,p391]
Nevertheless, despite the partial successes of the QFT approach, we saw above that Fuchs concluded in the same paper that: “However, [the FWB’s] final stage—a macroscopic, rotating cylinder with special optical properties through which two water currents run—still represents an interesting opportunity to further study and learn about the interactions of water with electric fields.” [Fuchs, 2010, p400]
It is that final stage of the FWB that seems to have eluded a full description by either EHD or quantum approaches. The key elements that remain to be fully explained include:
• annulus and core cylindrical structure;
• simultaneous bi-directional flows of water;
and
• rotation of the annular layer.
We have made reference above to the prime importance of electromagnetic effects in the behavior of the FWB. We will therefore compare the FWB with another cylindrical structure in which electromagnetic effects dominate the behavior.
The Behavior of a Plasma Birkeland Current
Plasma is the fourth state of matter and is now known to be the most common state of matter in the Universe outside Earth’s biosphere. [Rogoff, 1991, p989]
Plasma is sometimes described as an ionized gas. This is technically true, but reference to plasma as a form of gas does not reflect the complexity of the behavior of plasma under the influence of the electromagnetic forces inherent within it. It is that complexity which distinguishes plasma as a fourth state of matter, as distinct from solids, liquids and un-ionized gases.
Plasma behavior is governed by electro-magnetic laws. Maxwell’s Equations deter-mine the electric and magnetic fields resulting from the position and motion of charged particles. They also determine the interaction of the electric and magnetic fields if either is changing with time.
The Lorentz Force Law determines the electric and magnetic forces which each charged particle will experience due to the electromagnetic fields. The magnitude and direction of the Lorentz force depends on the strength of the fields, the charge on the individual particle, and the particle’s initial velocity. The response of the particle to the force also depends on its mass.
The resulting change in the position and velocity of each of the charged particles causes changes in the electric and magnetic fields.
Obviously this feedback loop can rapidly cause highly complex behavior which is extremely difficult to model mathematically. Simplifications are often introduced in order to enable solutions to be found.
However, these simplifying assumptions often lead to the omission of precisely those sorts of behavior which distinguish plasma from a gas. For example, EHD equations cannot model the complex behavior of plasma instabilities.
Nevertheless, the more stable states of plasma can be modelled by EHD equations provided that the inherent variability in all three dimensions is allowed for and is not ‘averaged out’ by over-simplification.
One common pattern of behavior unique to plasma is its ability to confine electrical current to a relatively narrow cylindrical region when transmitting the current through a large volume of plasma. The plasma rearranges itself under the influence of internal electromagnetic forces to form what is effectively an insulated cable around the current path. The remainder of the large volume of plasma is unaffected by the current. Fig. 1 below shows a typical example of this behavior in action.

Figure 1: An example of a Birkeland Current in space. Image credit: NASA / William P. Blair and Ravi Sankrit (Johns Hopkins University)
Plasma achieves this by forming a cylindrical double layer or sheath on the outside of the axial current filament. The double layer consists of adjacent cylindrical layers of positive and negative charge. Together, these generate a radial electric field which ensures no net current across the double layer. [Peratt, 1992, 5.5.1]
This filamentary arrangement is known as a Birkeland Current (BC).
The zone within the double layer is also governed by Maxwell’s Equations and the Lorentz Force Law applied to the individual charged particles in the filament, as explained below by reference to Fig. 2.
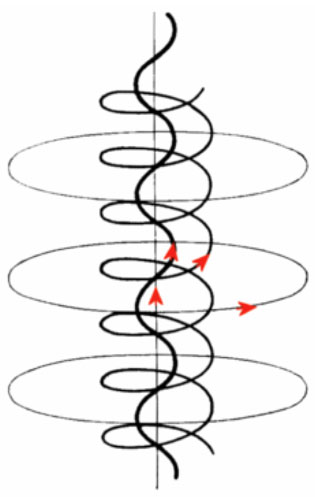
Figure 2: Magnetic Field Lines in a Birkeland Current [After Peratt 1992, Fig. 4.28] The external field Bz is vertically upwards in the figure. Three separate magnetic field lines resulting from the interaction of a current Iz flowing under the influence of an electric field Ez are shown. The degree of helicity of the net magnetic field lines is radially dependent. Due to the I x B vector cross product, the charge carriers (current) are constrained to follow the net magnetic field lines at any given radius.
According to Peratt [1992, 4.6.3], the net result of the interaction of the Lorentz Force and the electromagnetic fields generated by the moving particles themselves is a spiraling filamentary pattern in which the circularity of the paths of the particles is dependent on their radial distance from the axis of the filament.
In this magnetic field pattern, any current element which is slightly misaligned with the magnetic field in its locality will experience a radial Lorentz force which will shift the current element towards or away from the axis to a zone with greater or lesser degree of helicity. This automatically happens in such as way to ensure that the two vectors are re-aligned.
This gives rise to the alternative nomenclature for a Birkeland Current as a “Field-aligned Current” in which the I x B vector cross-product disappears and the arrangement is free of Lorentz forces.
The force-free configuration represents a minimum-energy state [Peratt, 1992, 1.7.2] and therefore it has inherent stability. The outer azimuthal (ring) magnetic field generated principally by the inner axial core of current effectively acts to constrain the filament and minor lateral disturbances are restored by the field forces.
Peratt says of the force-free configuration in a Birkeland Current: “It proves the stability of force-free fields and shows that in a system in which the magnetic forces are dominant and in which there is a mechanism to dissipate the fluid motion, force-free fields .. are the natural end configuration.” [Peratt, 1992, p29, s1.7.2]
It is also the most efficient direction for current to travel in through a magnetic field. The Lorentz Force Law effectively imposes an electrical resistance on motion transverse to the magnetic field by acting on particles moving in that direction due to the Lorentz Force. The resistance is therefore lowest in the direction parallel to the magnetic field lines where the Lorentz Force is absent.
Note especially the radial dependence of the direction of motion of the particles, which will be of importance for the remainder of this paper. The outer layers of the filament follow the more helical paths, which effectively imposes a spiraling motion on the flow of particles.
A further point is that plasma behavior is known to be scalable over many orders of magnitude. The behavior of plasma in space is based on exactly the same laws that apply in the laboratory and those same laws will influence the behavior of charged particles in other situations, regardless of scale.
Finally, plasma behavior is also exhibited by partially-ionized gases in which only a very small proportion of the gas is ionized. The magnitude of the electromagnetic forces in comparison to the gravitational and fluid dynamic forces ensures that the motions of the charged particles dominate the overall behavior.
We suggest that the same principle applies to the partially-ionized liquid of the FWB. In other words, a small proportion of charged particles in the FWB will have a disproportionate effect on the behavior of the whole structure.
Comparison of the Characteristics of a Birkeland Current (BC) in Plasma and the FWB
Obvious similarities between the characteristics of a Birkeland Current in plasma and the FWB include the following:
• Filamentary cylindrical structure.
• Applied axial electric field and resulting axial current. In both cases, an external driving electric field generates an axial current along the filament.
• Helical motion of the outer layer compared to the inner layer.
• A radial electric field. According to Armstrong, [quoted in Fuchs, 2010, p394],the FWB has a positively-charged outer layer and negative core; a BC has a confining Double Layer. In both cases, a radial electric field is formed. This radial electric field is fundamental to generating the azimuthal or rotational forces.
• Bi-directional transport. The FWB, in its final stable form, has equal water flow rates in both directions but appears to transport a net charge in one direction. Current in a BC is carried by both ions and electrons, which flow in opposite directions.
Discussion of the Stable Form of the FWB with reference to BC Dynamics
In the final stable state of the FWB, mass transport of water occurs simultaneously in both directions. “The water bridge reveals a multilayered structure with mass transport mainly [initially] from the anode to the cathode beaker, a backflow preventing the cathodic beaker from overflowing thereby stabilizing the phenomenon for hours.” [Fuchs, 2010, p397]
Charge transport across the bridge also occurs. Although experiments start with de-ionized water, it is clear from tests with pH dyes added after the experiment that charge has been created and transported. Fuchs states: “ .. there is a charge transport mechanism next to the electrochemical one, ..” [Fuchs, 2010, p399] and demonstrates that operation of the bridge results in a redistribution of charge between the beakers.
The obvious possibilities for the charge carriers are protons (H+), and hydroxide ions (OH–). [Fuchs, 2010, p282]
“The bridge had a reddish colour during all the experiments, indicating that protons were the main charge carriers.” [Fuchs et al, 2008, p2]
Less obviously, electrons (e–) may also be present in significant numbers, despite Castellanos’ assumption that they are normally very short-lived in liquids [see Fuchs, 2010, p400]
A recent study by Mucke et al (2010) has shown that free electrons may be more numerous in water than previously supposed. They identified “a hitherto unrecognized extra source of low-energy electrons produced by a non-local auto-ionization process called intermolecular coulombic decay” which is stimulated by UV light. [Mucke et al, 2010, p143]
The movement of any free electrons is unlikely to be significant in terms of the bulk transport of water across the FWB because electrons will not induce significant viscous drag on the neutral heavier water molecules. However, the electrons may play a significant role in the formation of the FWB by initiating the helical particle paths.
Dipole forces on neutral water molecules may also be relevant, as suggested by Fuchs: “… a dipole in the medium experiences a force towards higher field strength. … Since the main flow direction of the water bridge is polarity dependent but there is also always a flow in both directions, both effects [Coulomb electrophoresis & dipolar dielectrophoresis] have to be taken into consideration.” [Fuchs, 2010, p386]
However, the dielectrophoresis effect does depend on the presence of an electric field gradient which will be minimal in a perfectly cylindrical bridge.
Therefore the transport of water in both directions is likely to be indicative of transport of the ions H+ and OH- under the influence of the applied electric field, together with viscous drag of neutral molecules.
The simultaneous bi-directional flows towards the cathode and anode appear to be in the core and outer annulus of the FWB respectively.
There is some evidence that the outer rotating layer of an established FWB is positively charged, suggestive of this layer containing a predominance of H+ ions.
“Moreover, Lord Armstrong noticed a water flow in both directions, which he associated with a charge transport: ‘…the facts of the case seem to demonstrate that the negative current flows inside of the positive …’” [Fuchs, 2010, p394]
Further support for this view can be found in the observation that the outer layer rotates clockwise when viewed towards the cathode, consistent with the direction of the magnetic field formed around an axial current in the core.
The clockwise rotation is seen to be in the form of a spiral towards the cathode. [Marin & Lohseb, 2010 p16] It will therefore result in the observed bulk transport in that direction.
The core, therefore, must be supposed to be net negative and contain the OH– ions. That being the case, there will be a radial electric field between the outer rotating zone and the inner core.
The radial electric field will tend to counter the centrifugal forces on the outer layer and contribute to the stability of the bridge. Fuchs et al. have already noted the stabilizing effect of an azimuthal magnetic field around an axial current.
“The current causes a magnetic field along the capillary bridge to rise which focuses the electric field resulting in a thick and stable bridge” [Fuchs et al, 2011 p6] and also the stabilizing effect of rotation: “…the high-speed visualization revealed a rotation of the outer bridge layer, which provides additional stability to the bridge.” [Fuchs et al, 2008, p3] although the reasoning behind this last point is not explained.
The radial electric field between the positive annulus and the negative core drives the rotation. The vector cross-product Er x Bz of the radial electric field Er between annulus and core and the axial magnetic field Bz results in a tangential force and thence a velocity vφ which amounts to rotation of the annulus.
Considering the axial stability of the bridge, Fuchs has noted the stable equilibrium between surface tension & ordered dipole bonding caused by a high applied electric field. [Fuchs et al, 2007, p6114]
The surface tension must also be balanced in the azimuthal or tangential direction. Two distinct forces will contribute to this balance in the proposed model.
Firstly, the rotation of the outer annulus will cause a ‘centrifugal force’. Secondly, rotation of a charged ring generates both an axial magnetic field and a radial magnetic field gradient; the latter tends to expand the ring carrying the current. Both effects will act to mobilise the tangential surface tension.
Therefore the bridge may act as a stressed skin structure under tension in both directions. The bridge’s stiffness will be enhanced due to its stressed skin.
This effect may explain the current discrepancy between the very large axial electric field necessary to rearrange Hydrogen-bonded clusters into linear chains and the much smaller field actually necessary to ensure bridge stability.
There is a further effect of the rotating outer layer which may also be important.
As discussed above, the rotating positively-charged outer layer is effectively an azimuthal current. By the Biot-Savart Law, it will create an axial magnetic field in the same direction as the applied electric field.
Therefore the FWB appears to be operating under the same type of field-aligned regime as a Birkeland Current, as indicated in Fig. 3 below. If this is the case, we can expect this arrangement to be tending towards a force-free state which is inherently stable and a natural outcome of the electromagnetic forces in the bridge.
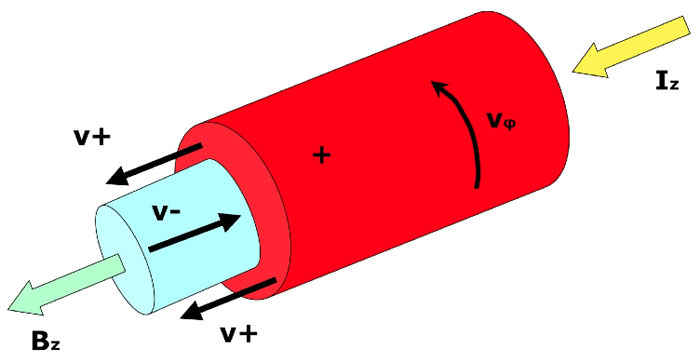
Figure 3: Summary of Plasma-like characteristics of the FWB; see text for details.
It must be acknowledged that the precise nature of the balance of electromagnetic forces cannot be exactly the same in the water bridge and the plasma Birkeland Current because the media are different. In particular, counter-flowing positive and negative charged particles in the water bridge cannot follow virtually the same paths in opposite directions because of viscous forces. In a BC, by contrast, the separation of protons and electrons can be much smaller.
This probably explains the development of an annulus and core structure in water in response to forces which generate the helical pattern in plasma.
Nevertheless, the similarities are so striking that it appears as though similar forces are being generated. The characteristics of the final form suggest that the bridge, consisting of a partially-ionized fluid, is achieving a similar balance of electromagnetic forces as an ionized plasma does in similar circumstances.
Furthermore, the bridge may also be an efficient charge transport mechanism due to the enhancement of the current and associated viscous drag by the Schönherr Whirl Stability effect in which a significant increase in current is achieved when a conductor is rotated about its axis.[see Peratt, 1992, 2.5.7 p58]
Discussion
The above analysis offers some additional insights as to the response of the ‘final form’ of the FWB to an applied electric field. In particular:
• The charge-separated Annulus and Core arrangement probably develops in tandem with the growth of a radial electric field and the start of rotation of the Annulus.
• Rotation of the positively-charged Annulus combined with axial current flow mirrors the particle paths in a Birkeland Current, which allows development of an axial magnetic field and radial magnetic field gradient.
• The field-aligned nature of the final form results in an efficient flow mechanism; the charge separation of the heavy ions into Annulus and Core allows simultaneous bi-directional flow, augmented by viscous drag of neutral water molecules.
• The combination of the radial magnetic field gradient together with centrifugal forces mobilzes the water bridge surface tension in the tangential direction. The axial electric field mobilizes the axial surface tension. In combination, the result is a stressed skin structure of high stability.
The above analysis offers an explanation of the anomalous behavior of the FWB which is unexplained by other analyses, including those based on EHD but where the radial variations are averaged out or assumed to be concentrated on the surface layer alone.
Conclusions and Future Research
The hypothesis presented in this paper is that the apparently anomalous behavior of partially-ionized liquids can be understood by applying the principles of ionized-gas plasma to the charged particles in the liquid.
In doing so, it is important to take into account the variability of the electromagnetic forces and the response of the charged particles in all three spatial dimensions. Approximations applied to the EHD or QED equations, whether of averaging or localization of effects into surface layers, will not model accurately the complexity of the actual behavior.
This paper has shown that the anomalous behavior of the Floating Water Bridge can be explained qualitatively by the suggested approach. The correspondence found between the behavior of the FWB and Birkeland Currents in plasma suggests that the basic approach is valid.
However, further experiments will be necessary in order to prove the hypothesis and provide quantification of the effects. Primary areas for future investigation include measurement of the magnetic field in and around the FWB; confirmation of the nature of the charge carriers and their separation into positive annulus and negative core; and investigation of the possible role of free electrons in the bridge dynamics.
Subsequent parts of this paper already in preparation will explore the application of plasma principles to biological situations involving plant sap flow and mammalian blood flow which also exhibit anomalous behavior.
References
Burcham CL, Saville DA (2002). Electrohydrodynamic stability: Taylor–Melcher theory for a liquid bridge suspended in a dielectric gas. J. Fluid Mech. 452: 163–187
Del Giudice E, Fuchs EC, Vitiello G (2010). Collective Molecular Dynamics of a Floating Water Bridge. Water 2: 69–82
Fuchs EC (2010). Can a Century Old Experiment Reveal Hidden Properties of Water? Water 2: 381-410
Fuchs EC, Woisetschläger J, Gatterer K, Maier E, Pecnik R, Holler G, Eisenkölbl H (2007). The Floating Water Bridge. J. Phys. D: Appl. Phys. 40: 6112–6114
Fuchs EC, Gatterer K, Holler G, Woisetschläger J (2008). Dynamics of the Floating Water Bridge. J. Phys. D: Appl. Phys. 41: 185502: 1-5
Fuchs EC, Agostinho LLF, Wexler A, Wagterveld RM, Tuinstra J, Woisetschläger J (2011). The behaviour of a floating water bridge under reduced gravity conditions. J. Phys. D: Appl. Phys. 44: 025501: 1-8
Marín ÁG, Lohseb D (2010). Building water bridges in air: Electrohydrodynamics of the floating water bridge. Phys. Fluids 22: 122104: 1-9
Melcher JR, Taylor GI (1969). Electrohydrodynamics: A Review of the Role of Interfacial Shear Stresses. Ann Rev Fluid Mech 1: 111-146
Mucke M, Braune M, Barth S, Förstel1 M, Lischke T, Ulrich V, ArionT, Becker U, Bradshaw A, Hergenhahn U (2010). A hitherto unrecognized source of low-energy electrons in water. Nature Physics 6: 143 – 146
Peratt AL (1992) Physics of the Plasma Universe, Chs. 1,2 & 4. Springer-Verlag, ISBN 0-387-97575-6
Rai D, Kulkarnia AD, Gejji SP, Pathak RK (2008). Water clusters (H 2O)n, n = 6–8, in external electric fields. J. Chem. Phys. 128: 034310: 1-14
Rogoff GL (Ed.) (Dec. 1991). IEEE Transactions on Plasma Science. 19: 989, from extract at http://www.plasmacoalition.org/what.htm
Saville DA (1997). ELECTROHYDRODYNAMICS: The Taylor-Melcher Leaky Dielectric Model. Annu. Rev. Fluid Mech. 29: 27–64
Widom A, Swain J, Silverberg J, Sivasubramanian S, Srivastava YN (2009). Theory of the Maxwell pressure tensor and the tension in a water bridge. Phys. Rev. E 80, 016301: 1-7
Discussion with Reviewers
Anonymous Reviewer: From what experimental or theoretical evidence [does] the author conclude that the core of the water bridge does carry negative charge and is not electrically neutral water?
R. Johnson: No detailed knowledge about the core can be found in the literature but inferences can be drawn from published experiments.
The question implicitly contrasts the core with the rotating positively-charged annulus. The thickness of the annulus has been estimated to be ~10-20% of the bridge’s radius. [Fuchs et al, 2008, p5] The core area therefore represents ~70% of the total cross-section of the FWB.
In water, OH– and H+ ions permanently dissociate and re-combine. OH– ions in the cathode beaker will be subject to Coulomb attraction across the bridge towards the anode due to the applied potential difference; therefore OH– ions are likely to be present in the core.
The electrically-driven bulk flow in the annulus towards the cathode is balanced by a return flow. If the core is neutral then this return flow can only be driven by the very small (~6mm) hydraulic head difference between the beakers, which must also overcome viscous drag from the annular layer. If the core contains negative charge then the counter-flow would be electrically-driven.
Fuchs 2010 p395 Fig 11 shows the lemniscate-shaped flows from anode to cathode and back. The positive and negative flow patterns are approximately symmetrical which suggests that they arise from the same cause. In other words, the return flow seems to be the negative counterpart of the positive ion flow from anode to cathode, not a hydraulically-driven flow across the bridge.
Experiments show that there is a narrow shear layer between the rotating annulus and the non-rotating core. [Fuchs et al, 2008, p4]
If the core was electrically neutral, one would expect that rotational viscous drag would distribute the shear layer throughout the core. The core would be accelerated until it was rotating at the same angular velocity as the annulus.
Apparently, some other force prevents this occurring and provides the balancing azimuthal force necessary to maintain a narrow annular shear layer at the interface.
Theoretically, if the proposed analogy with a Birkeland Current in plasma is valid, a spiral flow pattern of the charged particles and a self-sustaining radial electric field distribution in a bi-directional flow should be expected. However, as suggested in the paper, the fact that the phenomenon is occurring in a liquid, not a plasma, will modify the resulting flow pattern and may explain the clear separation of charge into a positive annulus and a (postulated) negative core. This would result in a radial electric field distribution which can explain the rotating annulus with non-rotating core, and the return flow, as observed.
To summarize, the suggestion that the core of the FWB probably contains negative ions is made on the following basis:
• the suggestion is not inconsistent with the reported experimental evidence;
• the applied electric field will tend to draw OH– ions into the bridge;
• a negative core offers a realistic mechanism for driving the return flow and for maintaining a narrow shear layer between the rotating annulus and non-rotating core;
• an electrically-driven return flow is consistent with the observed flow patterns;
• the alternative of a neutral core cannot explain these features;
and
• a negative core may be expected on theoretical grounds if the proposed analogy with plasma behavior is correct.
It is for these reasons that the paper concludes that primary areas for future research should include confirmation both of the nature of the charge carriers, and their postulated separation into a positive annulus and a negative core in the FWB.
Reviewer: It would be instructive to deter-mine whether various types of electrolytes in the FWB are segregated into different cylindrical layers as elements are in Marklund convection.
Johnson: This suggestion touches on the discussion above. There are similarities between Marklund Convection and the FWB to the extent that radial electric fields are a feature of the cylindrical structure of the flow regions in both cases.
However, the segregation caused by Marklund Convection results from the effect of the radial electric field generated within a Birkeland Current on the surrounding bulk plasma outside the current cylinder itself. Because the FWB experiments are performed in air or other dielectric media, Marklund Convection is unlikely to be evident in those experiments because the necessary source of ionized elements outside the flow zone is largely absent.
