 Collective Molecular Dynamics of a Floating Water Bridge
Collective Molecular Dynamics of a Floating Water Bridge
Del Giudice, E1; Fuchs, E C2,*; Vitiello, G3
Received 5 May 2010; revised 18 July; accepted 19 July. Published 30 July 2010; amended online 15 August 2010
Summary
When a high voltage is applied to pure water filling two beakers kept close to each other, a connection forms spontaneously, giving the impression of a floating water bridge. This phenomenon is of special interest, since it comprises a number of phenomena currently tackled in modern water science. The formation and the main properties of this floating water bridge are analyzed in the conceptual framework of quantum electrodynamics. The necessary conditions for the formation are investigated as well as the time evolution of the dynamics. The predictions are found in agreement with the observations.
Article Outline
Introduction
In 1893 Sir William Armstrong placed a cotton thread between two wine glasses filled with chemically pure water. After applying a high voltage, a watery connection formed between the two glasses, and after some time, the cotton thread was pulled into one of the glasses, leaving, for a few seconds, a rope of water suspended between the lips of the two glasses [1].
As a gimmick from the early days of electricity, this experiment was handed down through history until the present authors learned about it from W. Uhlig, ETH Zürich [2]. Although easy to reproduce, this watery connection between the two beakers, which is further referred to as ’floating water bridge’ holds a number of interesting static and dynamic phenomena [3,4,5,6,7,8,9].
At the macroscopic scale, several of these phenomena can be explained by modern electrohydrodynamics, analyzing the motion of fluids in electric fields (see, e.g., the Maxwell pressure tensor considerations by Widom et al. [10], or the book of Castellanos [11]), while on the molecular scale, water can be described by quantum mechanics (e.g., [12,13]).
The gap at the mesoscopic scale is bridged by a number of theories, such as quantum mechanical entanglement and coherent structures in water. These theories are currently discussed (e.g., [14,21,22,17,25]). Recently, a 2D neutron-scattering study indicated a low-level long-range molecular ordering within a D2O bridge [8]. Detailed optical measurements [7] suggested the existence of a mesoscopic bubble network within the water bridge.
The properties of water at these scales have drawn special attention due to their suggested importance to human physiology [15]. In this paper, we consider the interaction of an applied high voltage potential with the water molecules by exploring the suitability of a quantum field theory approach. In particular, we consider a quantum electrodynamics (QED) approach to the structure of liquid water proposed in refs. [23,24,25].
The paper is organized as follows. In section 2 the experimental set-up and the measurement methods are described, in section 3 the appearance of coherent structures in liquid water as an outcome of QED is discussed. In Section 4 we analyze in the same framework the formation of a mesoscopic/macroscopic vortex in liquid water as a consequence of the application of high voltage.
Sections 5 and 6 are devoted to the analysis of the process of formation of the water bridge, including a comparison between theory and experiment, and to the understanding of some of its properties, respectively. Some conclusions are finally drawn in Section 7.
Experimental
For the high speed imaging experiments performed, flat platinum electrodes were submerged in the center of the beakers, one set to ground potential (cathode), the other on high voltage, up to 25kV dc (anode). For the thermographic measurements, cylindrical silver electrodes were used. The beakers were filled with deionized H2O (‘milli-Q’ water, conductivity < 1μS/cm).
A Phywe high–voltage (HV) power supply (’Hochspannungs–Netzgerät 25kV’, Order No 13671.93) was used with a 42nF ceramic capacitor connected in parallel to the electrodes. The voltage was measured by a potential divider of 500MΩ/500kΩ to ground level. Since the voltage generator provided a limited current output, the electric current was stable at 0.5 mA, while the voltage continuously adapted. The images in Fig. 1 and Fig. 2 were recorded with a FLIR 620 thermographic camera (FLIR Systems, Boston, MA, USA).
The images in Fig. 3 and 4 were recorded with a Photron SA-1 high-speed camera (Photron Ldt, Bucks, United Kingdom). Fig. 3 was recorded with 2000 fps exposure time, after 0 ms (a, reference point), 198 ms (b) 268 ms (c) 306 ms (d) 536 ms (e) 551 ms (f) 626 ms (g) and 1020 ms (h). Fig. 4 was recorded with 1000 fps, 1/1000 s exposure time, after 0 ms (a), reference point), 510 ms (b) 520 ms (c) 570 ms (d) and 630 ms (e). In all cases, the high voltage was manually increased from 0 to 15 kV (+) dc, and the images were taken at the moment of bridge or vortex creation, respectively, which was between 7 and 11 kV.
Coherent Structures in Liquid Water
In this section we focus our attention on the gauge invariant properties of a system, like the water bridge, which exhibits complex dynamics. A key motivation for this approach arises from the fact that gauge invariance is the basic requirement to be satisfied when dealing with systems where charge density and electric polarization density play a relevant role.
It is apparent that the discussion of the gauge invariant properties can be done only within a field description of the structure and dynamics of water. As a matter of fact, many models introduced so far to describe water are based on molecular dynamics, which is an approximation that does not consider the field features of water (for reviews see e.g., [26,27]).
A conceptual step in this direction was the experimental proof for quantum entanglement in liquid water at room temperature: Chatzidimitriou–Dreismann et al. (1995) did Raman light-scattering experiments [16] on liquid H2O – D2O mixtures, which provided experimental evidence for the quantum entanglement of the ion OH– (and OD–) vibrational states.
In 1997, a first experimental proof of nuclear quantum entanglement in liquid water [17] was published, again, by Chatzidimitriou–Dreismann et al. by the means of inelastic neutron scattering. The interpretation is disputed [18,19]. Another approach where water is considered a ‘hot quantum liquid’ was proposed in 2006 [20].
In the frame of the theory of liquids, the model of liquid helium proposed by Landau [28] is appealing. Within this model the liquid appears as made up of two phases, one coherent (having components oscillating in phase), the wother non-coherent (having independent components as in a gas). There is no sharp space separation between the two phases since a continuous crossover of molecules occurs between them. This dynamical feature makes the experimental detection of the two-phase structure a delicate task indeed.
As a matter of fact, an experimental probe – that has a resolution time longer than the typical period of the particle oscillation between the two phases – produces a picture that is an average of the conformations assumed by the system during this time. This produces the appearance of a homogenous liquid [29,30]. On the contrary, the two-phase structure would only be completely revealed by an instantaneous measurement. In a realistic situation, an observation lasting a short-enough time could give evidence of the chunks of the coherent phase, which could succeed in remaining coherent during the whole time of the measurement.
This kind of observation would give some evidence of the existence of a two-phase structure, but would not be enough to give the full instantaneous extension of the coherent region. Recently, two articles [31,32] in favor of the proposed model appeared. In ref. [31] evidence is presented of two phases of water having different densities and orderings. Ref. [32] discusses a comprehensive account of the experimental data supporting the existence in liquid water of aggregates quite larger than those accountable in terms of customary electrostatic theories. In the frame of QED [23,24,25], a description of liquid water exhibiting two interspersed phases in agreement with these last experimental findings has been worked out. The two phases are:
i) a coherent phase made up of extended regions, the so-called “coherence domains” (from now on referred to as CDs) where all water molecules oscillate in phase between two configurations.
ii) ii) a non-coherent phase made up of independent molecules trapped in the interstices among the CDs.
The coherent oscillations of the molecules belonging to the first phase are maintained by the electromagnetic (e.m.) field self-produced and self-trapped within the CD, and occur between two definite molecule states. So far two such processes have been identified:
a) In a process analyzed in Ref. [23,24], the oscillations occur between two rotational levels of the water molecule. This produces correlations as large as several hundred microns. This also gives rise to a common dipole orientation of the molecule electric dipoles which, as a consequence of the rotational invariance of the aqueous system, gives rise to a zero net polarization. However, when the rotational symmetry is broken by an externally applied polarization field, such as that which occurs near a hydrophilic membrane or near a polar molecule, a permanent polarization develops. The range of permanent polarization depends on the amplitude of the external polarization field and, therefore, on the physical state of the surface. The application of a voltage would obviously increase this kind of correlation.
b) In a process analyzed in Ref. [25], the oscillations occur between the ground electronic state of the molecule and the excited 5d state at Eexc=12.06 eV, just below the ionization threshold at 12.60 eV. Each CD has a size given by the wavelength of the resonating e.m. mode
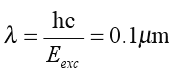 .
.
The frequency of the common oscillation of molecules and field is 0.26 eV (in energy units) at T = 0K, much lower than the frequency, 12.06 eV, of the free field. This dramatic softening of the e.m. mode is just the consequence of the nonlinear dynamics occurring in the process [23,25,24].
Non-aqueous molecules cannot participate in the resonant dynamics, so they are excluded from the CDs. In particular, atmospheric gases are expelled from the CD volume and give rise to nano- and/or micro-bubbles adjacent to the CD. When the dynamics causes a decoherence of a CD, such bubbles, too, would disappear, since their components are able to dissolve again in the non-coherent fraction of water.
The amount of the coherent fraction in the liquid is decreasing with temperature. At room temperature the two fractions are approximately equal [25]. In the bulk water, molecules are subjected to two opposite dynamics: the electrodynamical attraction produced by coherence and the disruptive effect of the thermal collisions, so that, whereas in the average the relative fractions are time independent, at a local, microscopic level each molecule is oscillating between the coherent and the non-coherent regime. The coherent structure is thus a flickering one, so that an experiment having a duration longer than the lifetime of a CD probes water as a homogenous medium.
In the coherent state in the fundamental configuration, whose weight is 0.87, all the electrons are tightly bound, whereas in the excited configuration, whose weight is 0.13, there is one quasi-free electron. Consequently, a CD contains a reservoir of 0.13 x n quasi-free electrons. At room temperature n is about 6 x 106. In Ref. [33] it has been shown that this reservoir can be excited, producing cold vortices of quasi-free electrons confined in the CD.
The energy spectrum of these vortices can be estimated following the mathematical scheme outlined in ref. [33]. Similarly, it can be seen that the lowest lying excited state has a rotational frequency of a few kHz and the spacing of the levels has the same order of magnitude. The lifetime of these vortices can be extremely long because coherence prevents random (thermal) fluctuations and because the conservation of the topological charge prevents the decay of the vortex in a topologically trivial state.
We finally remark that in a coherent region, the pure gauge nature of the e.m. potential field
(1) ![]()
where λ is the gauge transformation function, implies that the applied electric potential V is proportional to the time derivative of the phase Φ (see below): ![]() . Here and throughout the paper we omit the space-time dependence of the variables whenever no misunderstanding arises therefrom. When necessary we adopt the notation x ≡ (x,t).
. Here and throughout the paper we omit the space-time dependence of the variables whenever no misunderstanding arises therefrom. When necessary we adopt the notation x ≡ (x,t).
The two above-mentioned dynamics occur simultaneously and produce a non-trivial interplay that gives rise to a number of phenomenological situations:
1) Bulk water in normal conditions. In this case, the dynamics a) are phenomenologically irrelevant due to the rotational symmetry of the system. The dynamics b) only are at work, producing instant CD structures as large as 0.1μm, which are exposed to the disruption of the thermal collisions.
This gives rise to a Landau-like situation where water appears homogeneous in experiments having a long-enough resolution time and exhibiting deviations from homogeneity at smaller resolution times. Moreover, the flickering nature of the coherent structure prevents the appearance of the long time features of the coherent dynamics.
In the case of the bulk water, the experimental check of the theory is the correct prediction of the thermodynamic processes, which do not depend on the space distribution of the coherent molecules, but on their total number only. The flickering space structure of CDs implies that the corresponding ensemble of microbubbles described above should be a flickering one too, as found by the experimental observations.
2) Interfacial water. In this case, dynamics a) are at work and their interplay with dynamics b) gives rise through nonlinear dynamics to a stabilization of the coherent structure, which is much more protected against thermal fluctuations.
The equilibrium between the two phases is shifted toward coherence. Since an extra energy gap is added, molecules are kept aligned by the total polarization field produced by the dynamics a) that compels the radiative dipoles produced by the dynamics b) to stay aligned.
The smaller CDs (0.1 μm) of dynamics b) are tuned together by the much more extended coherence produced by dynamics a), so that the global coherent region, thanks to the polarization field produced by the surface, gets widened up to several hundreds of microns. This is the span of the CD dynamics a). A confirmation of this QED prediction is provided by the experimental findings of the group led by G. H. Pollack [34], which confirm results obtained more than sixty years earlier [35]. They show that layers of “anomalous” water (EZ water) as thick as 500 μm appear on hydrophilic surfaces.
The observed anomalies include the exclusion of solutes, a highly reducing power (corresponding to a negative redox potential of several hundreds of millivolts), and widely different optical and electrical properties. These anomalies are compatible with those expected from the coherence domains of dynamics b) [25]. A much more detailed discussion of this important point will be given elsewhere.
3) Bulk water in special conditions. Ref. [36] describes the possibility of the onset of a coherence among CDs induced by the tuning of the phases of the oscillations of the CDs, which in normal water are not correlated. This tuning of the different CDs can also be induced by the application of an external e.m. field.
A recent 2D neutron scattering study indicated a preferred molecular orientation within a heavy water bridge [8]. This observation can be interpreted in accordance with the dynamics a). Moreover, this prediction could account for the experimental observation of a so called “Neowater” produced by an Israeli group [37] and compatible with similar results of Russian [38] and Ukrainian researchers [39]. This important point, too, will be discussed at length elsewhere.
The stabilization of the array of water CDs implies the stabilization of the corresponding ensemble of microbubbles, which therefore form a stable and ordered array. This result has been reported in Ref. [37]. Katzir et al. connect the ordered nature of the neowater structure with the appearance of the ordered network of microbubbles; they report as a typical size of the single microbubble a value comparable to the CD size. Thus QED provides a rationale for this surprising phenomenon.
However, the cases 2) and 3) are different. In the case 2) the superposition of the two coherent dynamics gives rise to a continuous coherent region, which doesn’t contain non-coherent zones. Therefore, the re are no bubbles. In case 3) there is a coherent ensemble of CD, which allows the presence of interstices and microbubbles. In this paper we concentrate on describing what happens in the particular case of the floating water bridge. This discussion will be done in the next section.
Formation of a Mesoscopic/Macroscopic Vortex
The formation of the floating water bridge is triggered by the application of a high voltage V. Let us discuss which are the consequences of such a physical operation on a coherent structure such as the one described in the previous section. We split the e.m. potential Aμ into the electric and magnetic part. In cgs units we have
(2) 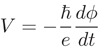
(3) ![]()
where e denotes the electron charge. According to Eq. (2) the application of a voltage implies a strong variation of the phase Φ which adds up to the original phase of the unperturbed CDs.
Should the applied potential be high, the voltage generated phase would be dominant with respect to the original phase, which might be regarded as a small perturbation of the total phase. The new phase spans over a macroscopic region and is thus space-correlating all the phases of the CDs enclosed in the macroscopic region. A coherence among the CDs emerges.
Moreover, in this new macroscopic coherent region, a definite non-vanishing gradient of the phase has appeared, that, in turn, according to Eq. (3), produces a non-vanishing magnetic potential.
The presence of a magnetic field depends on the rotational or irrotational character of the geometry of the problem. One can show [40, 41] that consistency with the gauge invariance requires that
(4) Φ(x) → Φ(x) – eα f (x)
where ἁ is a constant depending on the wave renormalization constant and the transformation function f(x) is a solution of the equation ∂2f(x) = 0. We use x ≡ (x,t). The macroscopic current ju,cl is given by [40, 41].
(5) 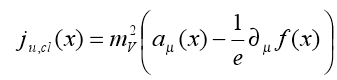
where a μ,cl(x) is the classical e.m. field, which has acquired the mass mv (the Anderson-Higgs-Kibble mechanism [42]). One has ∂μ jμ,cl(x) = 0.
It is crucial here to stress that the presence of quasi–free electrons in the elementary CDs fully characterizes the dynamical regime of the system. Since these quasi–free electrons are confined within the CDs, their motion is necessarily a closed one, which implies that a magnetic field is generated.
Moreover, the beaker system exhibits a local non-trivial topology. That is because the (charged) electrode in the beaker center prevents the paths closed around it from shrinking to zero. That is, of course, provided one does not draw these paths around the electrode tip. This fact produces a macroscopic vortex.
Such a vortex is indeed present in both beakers and can be visualized with a thermographic camera as shown in Fig. 1. Thus, an extended coherence, on a scale much larger than the original 0.1μm, is the consequence of the application of a high voltage. The extended coherence is also the consequence of the absence of an electric current, as can be seen in the short time just after engaging the voltage yet before the appearance of the bridge. This effect can be understood as a variant of the well-known Bohm–Aharonov effect [43].
Such a phenomenology is described in formal terms by the fact that the function f(x) may indeed carry a topological singularity describing the occurrence of a vortex and given by
(6) f(x) = arctan(x2/x1).
Eq. (6) shows that the phase is undefined on the line r = 0, with r2 = x12 + x22, consistently with the phase indeterminacy at the electrode site due to the specific system geometry.
When f(x) carries a (vortex) topological singularity, it means that it is path-dependent (not single-valued). When f(x) is a regular function, i.e., when it does not carry a topological singularity, the current ju,cl vanishes [40,41]. This, in turn, implies zero e.m. field Fμv = ∂μav – ∂vaμ.
In conclusion, in the dynamical scenario depicted above, the action of turning on the high potential compels the CDs to join the observed giant vortex, whose core position is determined by the electrode position. The closer the CDs are to the vortex core (the electrode), the stronger the action pushing them to join together.
Since the applied potential is a decreasing function of the distance from the electrode, peripheral CDs (those nearest to the beaker wall) have a better chance to preserve their individuality. (They are, however, in a non–equilibrium regime due to the criticality of the dynamics going on).
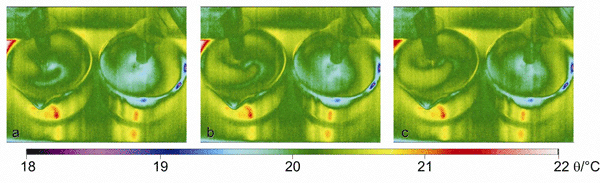
Figure 1: Thermographic visualization of the macroscopic Vortex in the beakers under application of high voltage before the water bridge is formed. The time interval between the images is 5 sec, the temperature scale is calibrated to the emissivity of water (0.96).
The presence of the other electrode in the grounded beaker—and the consequent existence of a preferred radial direction on the joining line between the two electrodes—breaks the cylindrical symmetry around each one of the electrodes.
The radial velocity of the slightly (~1K) colder vortices is ~ 1°/s – 3°/s and could be observed independently of the potential applied. The rotational direction was counter-clockwise in both beakers. In Fig. 2, the symmetry break due to the influence of the second beaker is visualized by thermography.
Fig. 2a again shows the slight cooling of the vortices. After a certain threshold (between 9 and 11kV), a cooling along the joining line of the electrodes as shown in Fig.2b appears (2-3K), and the rotation stops. The cooling is then followed by electric discharges heating the beaker walls (Fig. 2c) and finally leads to the water bridge formation (Fig. 2d). The dark spots on the anode in Fig. 2c and d are water droplets, which were ejected from the beakers during the process.
The vortices occur independently of the value of the applied potential. The potential acts as a trigger inducing the phase transition. The inner dynamics of the water then control the system evolution and its vorticity. This explains the observed independence of the turbulent patterns of the strength of the applied potential.
Finally, we note that the above description which starts from the analysis of the microscopic dynamics is consistent with the results obtainable by use of the classical electro–hydro–dynamics (EHD) field equations, originally proposed by Melcher and Taylor [44] and completed by Saville [45], describing the effects of a high voltage applied onto a ”leaky dielectric.”
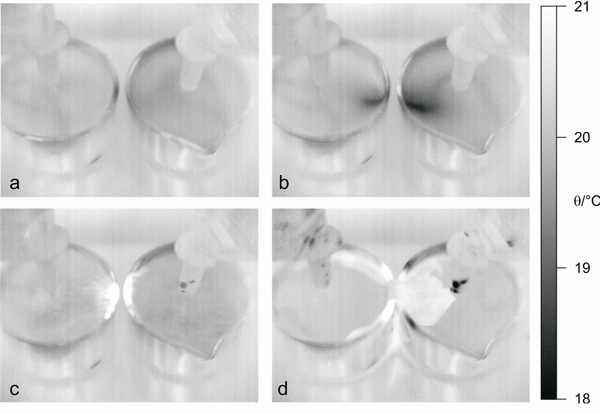
Figure 2: Thermographic visualization of the bridge formation mechanism. First, the macroscopic vortices appear (a), then the water cools down at the joining line of the two electrodes (b). With the first sparks (c), the water heats up, and finally forms a water bridge (d). The time interval between the images is 5s, the temperature scale is calibrated to the emissivity of water (0.96). The dark spots on the electrodes in (c) and (d) are water droplets which were ejected during the process.
Formation of the Water Bridge
It is well known [42] that within a coherent region a magnetic field should vanish (Meissner effect), provided that the size of the region exceeds a threshold (London penetration length). Indeed, the magnetic field penetration in the coherent region decays exponentially, as described by the London equation
(7) 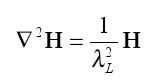
where λL is the London penetration length (see, e.g., Ref. [46]). This property is the consequence of the regularity of the phase in the coherent region (far from the boundaries), which produces the vanishing of the magnetic field [cf. Eq. (5) and the comments following Eq. (6)]. Near the boundaries the phase acquires a singular behavior due to inhomogeneities and this produces a non-vanishing magnetic field [cf. Eq. (6)].
In the case of liquid water, λL has a value much larger than the size 0.1μm of the water CD, in agreement with the well-known fact that magnetic fields are not expelled from normal water.
However, when the peculiar dynamics outlined in the previous section are at work, the coherent region could become so far extended that its size overcomes the London penetration length. In this case a phenomenon of levitation analogous to the one observed with superconductors might occur.
Actually, in the presence of the Meissner effect, a gradient of the magnetic inductance μ appears since μ = 0 in the coherent region and equals about one outside. A magnetic levitating force FlH = -H2gradμ appears, provided that H2 is inhomogeneous.
At the air water interface, the presence of the macroscopic vortex (described above) produces a high value of H2 below the water surfaces. Consider that, in the atmosphere above the surface, H2 is much lower and corresponds to the ambient magnetic field.
Consequently, a net upward force develops that raises the CD up. Since the extended coherent region is the one close to the beaker wall, magnetic levitation would occur along the wall of the vessel where the size of the coherent regions is larger. These magnetic forces would occur only in the vessel with the high positive potential where the vortex can develop.
In the grounded beaker, however, the high positive potential will be absent.
Moreover, an electric levitation force
(8) Fle = -E2gradε
may appear, since the dielectric constant ε is much larger in the CDs than in the non-coherent region. As a matter of fact, if we model the non-coherent region as an ensemble of independent electric dipoles, the Fröhlich formula would give us room temperature ε = 15. The dielectric constant of the CDs, in contrast, could be estimated to be 160 [47]. Since at room temperature the two fractions are almost equal, the two above estimates result in an average dielectric constant εobs of εobs = (160/2) + (15/2) = 87.5 which is in good agreement with the experiment.
Along the line joining the two electrodes, the electric field is very strong and reduced below the water surface by a factor 1/ε whereas it is at full strength above the air water surface. A net upward force is thus generated according to Eq. (8).
We conclude that the application of a high electric voltage, through the complex dynamics outlined above, gives rise to two levitations: electric and magnetic. These levitations occur along the wall of the vessel with the positive electrode. Only the electric levitation can occur in the grounded vessel.
This prediction is in agreement with the observation of a larger probability of water-column formation. The water-column formation occurs in the HV vessel rather than in the grounded vessel. This is shown by high-speed visualization in the examples given in Fig. 3 and Fig. 4. For both figures, fringe projection technique is used to contour the bridge and thus enhance its visibility (for details see [7]).
The levitating drops of water, being coherent, are surrounded by the evanescent electromagnetic field, filtering out of the coherent cores. The tail of the evanescent field spans for a length of the same order as the CD radius, so that it could act as an interaction field among the drops within some distant. This distance is in the order of the droplet radius, namely some microns. The possibility of the formation of a string of interacting water droplets emerges and eventually gives rise to the water bridge.

Figure 3: High speed visualization of the water bridge formation with glass beakers and fringe projection. (a) shows the beakers before the voltage is applied, (b) – (d) show the levitation of the water in both beakers leading to droplet formation, (e)–(f) show the ejection of a jet from the HV beaker leading to the bridge formation (g), which is stabilized in (h). The water on the HV side (right) is levitated stronger than on the grounded side (left) due to the fact that the water is lifted both electrically and magnetically there, whereas on the grounded side, the levitation is due to electric forces only.

Figure 4: High speed visualization of the water bridge formation with Teflon beakers with fringe projection. (a) shows the situation without high voltage, in (b) and (c) the fringe projection shows the rising of the surfaces, in (d) levitation and droplet formation are shown, and in (e) a connection is finally formed.
Properties of the Water Bridge
The water bridge thus represents a sequence of interacting coherent droplets extracted from the water vessels. The electron coherence illustrated in Section 3 points to the CDs as reservoirs of quasi free electrons. On the CD boundaries a ponderomotive force
(9) 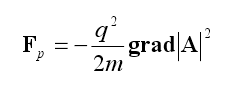
acts upon any particle having charge q and mass m present there. Eq. (9) can be easily understood considering that the Hamiltonian of a particle immersed in a vector potential gives rise to a field energy distribution
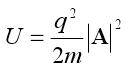
which produces in turn the force
Fp = –gradU
The ponderomotive force Eq. (9) pushes the quasi-free electrons outwards with a force many thousand times larger than that acting on the parent molecules. As a consequence, a double layer of charges appears on the boundary of the CDs. The applied strong electric field induces a twofold motion along the bridge. The positive cores of the CDs are pushed along the bridge from the anode to the cathode. This gives rise to a simultaneous transport of mass, whereas the outer, negatively charged, layer slides toward the cathode.
We should remember that the component droplets of the water bridge have been extracted from a macroscopic vortex so that their motion along the bridge arises from the superposition of the vortex motion and the electrically induced motion. The final result is a helicoidal motion around the axis of the bridge, a sort of traveling vortex.
According to the topological considerations developed in section 3, the axis of the bridge should be the site of a topological singularity. In other words, no coherence should exist on the axis. Consequently, a negative gradient of the coherent fraction should be observed when going from the outer surface to the axis of the bridge. This prediction is consistent with observation of a negative gradient of the speed of sound in the same direction [9]. Actually, since the coherent region is very much correlated, the speed of sound should be larger in the coherent region than in the non-coherent one.
The peculiar optical properties of the bridge are described in Ref. [7], with particular regard to the change of the polarization angle of linearly polarized light passing through the bridge. As suggested in Ref. [4], this change can be connected to both reflection at micro-bubbles under the Brewster angle [7], or, as shown in a very recent work, to birefringence due to long-range low-ordering within the bridge [8]. A detailed discussion of this in the framework of QED will be given elsewhere.
Experimental observations [7] have shown that cooling—achieved by, e.g., the addition of ice cubes to the beakers—destabilizes the bridge. This can be easily explained within the proposed model. The coherent fraction increases when temperature—and the depth of the interstices among them—decreases.
Consequently, the excitation of rotational motion of the CDs becomes more and more difficult. This is the result of the drag produced by the interaction with neighboring CDs through the evanescent fields protruding from inside of them.
At the freezing point, the drag becomes so intense that it prevents the formation of vortices. As explained above, the existence of these vortices is crucial for the presented analysis; their reduction explains the destabilization of the phenomenon.
Finally, the suggested ordered network of microbubbles would be a natural consequence of the presence of a permanent extended coherence as discussed in section 3.
Conclusions
Much work is still needed to understand the wealth of the results revealed by the water bridge. However, in this paper we have shown that a consistent framework for understanding this surprising phenomenon can be provided by QED.
Without a doubt, water is one of the most common and most studied substances in the world. The properties of water at mesoscopic scale have drawn special attention lately due to their suggested importance to human physiology [15].
Still, present theories have difficulties explaining more than a few of its properties at once, and no theory so far can satisfyingly explain one lately rediscovered phenomenon, the floating water bridge.
The QED approach to this phenomenon provides a possible theoretical background for many of the bridge’s features, such as the vortex formation upon applying a potential; the occurrence of a cold region prior to the rising of the water; the asymmetric rising of the water in the beakers; the stability of the bridge; the temperature dependence of this stability; the correlation of charge and mass transfer; the formation of micro and nanobubbles and consequently; and the findings by optical and neutron scattering
Therefore, although unconventional in the field of electro-hydro-dynamics (EHD), quantum field theory can be a powerful tool to bridge the gap between microscopic descriptions and field theories.
This has, until now, been conceived as a quite difficult task [11]. Moreover, some of the described effects can be found in other experiments as well, such as the macroscopic vortices discussed herein.
These vortices, hitherto unexplained, are known as EHDs. Furthermore, an application (as a motor) was discussed recently [48]. Also, the Pollack group suggested formation of a clear zone next to gel surfaces [15].
Recently, Cabane et al. stated that water has thus far been a fantastic ”graveyard” for theories that are clever but wrong [27]. It may be appropriate here to stress the well-known fact that no theory can in principle describe reality in all its aspects.
Nevertheless, to the knowledge of the authors, no other theory has been able to describe the floating water bridge as correctly, or in as precise detail, as the quantum field theory. Therefore, it may be prudent to assume that QED is a good choice to describe and understand this special interaction of water with electric fields.
Special Acknowledgments
The authors would like to express their gratitude to Prof. Jakob Woisetschläger for the performance of the presented experiments.
Acknowledgments
With great pleasure, the authors wish to thank Profs. Marie-Claire Bellissent-Funel (Laboratoire Léon Brillouin, Saclay), Eshel Ben-Jacob (Tel Aviv University), Cees Buisman (Wetsus – Centre of Excellence for Sustainable Water Technology), Friedemann Freund (NASA SETI Institute, Mountain View CA), Karl Gatterer (Graz University of Technology), Franz Heitmeir (Graz University of Technology), Jan C.M. Marijnissen (Delft University of Technology), Laurence Noirez (Laboratoire Léon Brillouin, CEA-CNRS/IRAMIS, CEA-Saclay), Gerald H. Pollack (University of Washington), Alan Soper (Rutherford Appleton Laboratories, Oxford), José Teixeira (Laboratoire Léon Brillouin, CEA-CNRS/IRAMIS, CEA/Saclay), as well as Luewton L.F. Agostinho, Ingo Leusbrock and Astrid H. Paulitsch-Fuchs (Wetsus, Centre of Excellence for Sustainable Water Technology) for the ongoing discussion on the water bridge phenomenon (in alphabetic order). Partial financial support from University of Salerno and Istituto Nazionale di Fisica Nucleareis also acknowledged.
References
[1] Armstrong, WG (10 February 1893). Electrical phenomena. The Newcastle Literary and Philosophical Society, The Electrical Engineer: 154-145.
[2] Uhlig, W (2005). Personal communication, Laboratory of Inorganic Chemistry, ETH Hönggerberg – HCI, CH-8093 Zürich.
[3] Fuchs, E C; Woisetschläger, J; Gatterer, K; Maier, E; Pecnik, R; Holler, G; Eisenkölbl, H (2007). J. Phys. D: Appl. Phys. 40: 6112-6114.
[4] Fuchs, E C; Gatterer, K; Holler, G; Woisetschläger, J (2008). J. Phys. D: Appl. Phys. 41 (2008) 185502-7.
[5] Fuchs, E C; Bitschnau, B; Woisetschläger, J; Maier, E; Beuneu, B; Teixeira, J (2009). J. Phys. D: Appl. Phys. 42: 065502-6
[6] Nishiumi, H; Honda, F (2009). Res. Let. Phys. Chem. art. ID 371650 (3pp).
[7] Woisetschläger, J; Gatterer, K; Fuchs, E C (2010). Exp Fluids 48: 121–131
[8] Fuchs E C, Baroni P, Bitschnau B, Noirez L, J. Phys. D: Appl. Phys. 43 (2010) 105502 (5pp).
[9] Fuchs E C, Bitschnau B, Di Fonzo S, Gessini A, Woisetschläger J, Bencivenga F, Inelastic UV scattering in an floating water bridge, in preparation.
[10] Widom A, Swain J, Silverberg J, Sivasubramanian S, Srivastava Y N, Phys. Rev. E 80 (2009) 016301 (7pp).
[11] Castellanos A, Electrohydrodynamics, International Centre for Mechanical Sciences, CISM Courses and Lectures No.380, Springer, Wien, New York, Ed. (1998), ISBN 3-211-83137-1.
[12] Mrázek J, Burda J V, J. Chem. Phys. 125 (2006) 194518.
[13] Jorgensen W L, Tirado-Rives J, PNAS Proc Natl Acad Sci. 102 (2005) 6685-6670.
[14] Del Giudice E, Journal of Physics: Conf. Ser. 67 (2006) 012006.
[15] Pollack G H (2001) Cells, Gels and the Engine of Life, Ebner and Sons, Seattle WA, USA, ISBN 0-9626895-2-1.
[16] Chatzidimitriou-Dreismann C A, Krieger U K, Möller A, and Stern M, Phys. Rev. Lett. 75 (1995) 3008.
[17] Chatzidimitriou-Dreismann C A, Redah T A, Streffer R M F, Mayers J, Phys. Rev. Lett. 79 (1997) 2839-2842.
[18] Torii H, Phys. Rev. Lett. 84, 5236 (2000).
[19] Chatzidimitriou-Dreismann C A, Abdul-Redah T, Kolaric B, and Juranic I, Reply: Phys. Rev. Lett. 84 (2000) 5237.
[20] Yoon B J, Second International Conference on Flow Dynamics (ed. Tokuyama M and Maruyama S), Conf. Proc. 832 (2006) 225-228.
[21] Head-Gordon T, Johnson M E, PNAS Proc. Natl. Acad. Sci. USA 21 (2006) 7973-7977
[22] Stanley H E, Buldyrev S V, Franzese G, Giovambattista N, Starr F W, Phil. Trans. R. Soc. A 363 (2005) 509-523
[23] Del Giudice E, Preparata G, Vitiello G, Phys. Rev. Lett. 61 (1988) 1085-1088.
[24] Del Giudice E, Vitiello G, Phys. Rev. A 74 (2006) 022105-9.
[25] Arani R, Bono I, Del Giudice E, Preparata G, Int. J. Mod. Phys. B 9 (1995) 1813-1841.
[26] Teixeira J, Luzar A, Physics of liquid water. Structure and dynamics, in “Hydration Processes in Biology: Theoretical and experimental approaches”, NATO ASI series, M.-C. Bellissent-Funel ed., (IOS Press, Amsterdam, 1999), 35-65.
[27] Cabane B, Vuilleumier R, C. R. Geoscience 337 (2005) 159-171.
[28] Landau L D, J. Physics USSR (Moscow) 5 (1941) 71.
[29] Hendricks R W, Mardon P G, Schaffer L B, J. Chem. Phys. 61 (1974) 319.
[30] Bosio L, Teixeira J, Stanley H E, Phys. Rev. Lett. 46 (1981) 597.
[31] Huan C, et al., PNAS Proc Natl Acad Sci. USA 106 (2009) 15241-6.
[32] Yinnon C, Yinnon T, Mod. Phys. Lett. B 23 (2009) 1959-1973.
[33] Del Giudice E, Preparata G, A new QED picture of water, in: Macroscopic quantum coherence, Sassaroli et al. Eds., World Scientific, Singapore (1998).
[34] Zheng J M, et al., Ad. Colloid. Interface Sci. 23 (2006) 19-27.
[35] Henniker J C, Rev. Mod. Phys. 21 (1949) 322-341.
[36] Del Giudice E, Tedeschi A, Electromagnetic Biology and Medicine 26 (2009) 48-54.
[37] Katzir Y, et al., J. Electrochem. Soc. 154 (2007) 249-259.
[38] Korotkov K et al, J. Appl. Phys. 95 (2004) 3334-3338.
[39] Andriewski G V, Klochkov V K, Derevyanchenko L I, Fullerenes, Nanotubes and Carbon Nanostructures 13 (2005) 363-376.
[40] Matsumoto H, Papastamatiou N J, Umezawa H, Vitiello G, Nucl. Phys. B 97 (1975) 61-89.
[41] Matsumoto H, Papastamatiou N J, Umezawa H, Nucl. Phys. B 97 (1975) 90-124.
[42] Anderson P W, Basic notions of condensed matter physics, Menlo Park, Benjamin (1984).
[43] Peshkin M, Tonomura A, The Aharonov-Bohm effect. Springer-Verlag (1989).
[44] Melcher J R, Taylor G I, Annu. Rev. Fluid. Mech. 1 (1969) 111-146.
[45] Saville D A, Annu. Rev. Fluid. Mech. 29 (1997) 27-64.
[46] Feynman R P, Statistical Mechanics, The Benjamin/Cummings Pub. Co., INC. Reading, MA (1972).
[47] Del Giudice E, Preparata G, unpublished.
[48] Sugiyama H, Ogura H, Otsubo Y, The Society of Rheology 80th Annual Meeting. AIP Conference Proceedings 1027 (2008) 1453-1455.
[49] Taylor F R S, Proc. R. Soc. Lond. A, Math. Phys. Sci. 280 (1964) 383–97.
[50] Hartman R P A, Brunner D J, Camelot D M A, Marijnissen J C M and Scarlett B, J. Aerosol Sci. 31 (2000) 65–95.
[51] Chaudhary K C and Redekopp L G, J. Fluid Mech. 96 (1980) 257–74.
[52] Ashgriz N and Mashayek F, J. Fluid Mech. 291 (1995) 163–90.
[53] Eggers J and Villermaux E, Rep. Prog. Phys. 71 (2008) 026601 1–79.
[54] Rai D, Kulkarni A D, Gejji S P and Pathak R K J. Chem. Phys. 128 (2008) 034310.
[55] Choi Y C, Pak C, Kim K S, J. Chem. Phys. 124 (2006) 094308.
[56] Teixeira J, Bellissent-Funel M-C, J. Phys.: Condens. Matter 2 (1990) SA105-SA108.
[57] Némethy G, Scheraga H A, J. Chem. Phys. 36 3382,3401 (1962); 41, 680 (1964).
[58] Walrafen G E, J. Chem. Phys. 47 (1967) 114.
[59] D’Arrigo G, Maisano G, Mallamace F, Migliardo P, Wanderlingh F, J. Chem. Phys. 75 (1981) 4264.
[60] Walrafen G E, Hokmabadi M S, Yang W-H, J. Chem. Phys. 85 (1986) 6964.
[61] Bartell L S, J. Phys. Chem. B 101 (1997) 7573.
[62] Cho C H, Singh S, Robinson G W, J. Chem. Phys. 107 (1997) 7979.
[63] Bellissent-Funel M-C, J. Teixeira, L. Bosio, J. Chem. Phys. 87 (1987) 2231.
[64] Bizid A, Bosio L, Defrain A, Oumezzine M, J. Chem. Phys. 87 (1987) 2225.
[65] Bellissent-Funel M-C, Europhys. Lett. 42 (1998) 161.
[66] Bellissent-Funel M-C, L. Bosio, J. Chem. Phys. 102 (1995) 3727.
Discussion With Reviewers
John D. Swain1 : In section IV there is the claim that the beaker system has a nontrivial topology, but this can’t quite be true since the volume of water in the beaker, even with the electrode excluding some, is contractible and thus topologically trivial in the strict sense of the term. I’m sure what is meant is that there is, in some sense, a locally nontrivial topology near the electrode—i.e., there are loops around the electrode which are sort of nontrivial in the sense that they can’t be shrunk to zero in a plane that is punctured by the electrode. But one can certainly shrink them if one pulls them around the tip. It might be better to say (if I understand the intention of the authors correctly) that there the topology is nontrivial in some local sense very near the electrode. (By “local” I mean that one does not allow loops drawn around the electrode to be pulled very far from it).
Emilio Del Giudice, Elmar C. Fuchs and Giuseppe Vitiello: We perfectly agree with the referee observation. Indeed, the beaker system exhibits a local non-trivial topology since the (charged) electrode in the beaker center prevents the paths closed around it from shrinking to zero (provided, of course, one does not pull these paths around the electrode tip). We have included a short sentence concerning this point in the paragraph after Eq. 5.
Swain: Equation 9 for the ponderomotive force is often written (in tex notation) as F=-\frac{q^2}{4m\omega^2} grad |\vec{E}|^2. This has the advantage of being gauge invariant. If one wants to write it in terms of the vector potential A, I suppose what is being assumed is A oscillating at frequency omega and E=-dA/dt being used with the other factor of 1/2 coming from some time averaging.
Is this correct? If so, one might want to consider writing it gauge invariantly, mentioning that the field is oscillating, and that an average is being taken. I know the ponderomotive force assumes a time-varying field, but this may not be immediately obvious to the reader who is not a bit of an expert.
At the moment, one has to know a fair bit of physics to see what this might mean. As it stands, for a general case, one could think that one could make a gauge transformation and get into all sorts of trouble. For example, around a solenoid one has no B, but clearly an A which cannot be made to vanish everywhere (Aharonov- Bohm effect) and still there would be no force—I think the assumed time dependence (if I understand this correctly) should be noted.
Similarly, the energy being U=\frac{q^2}{2m}||\vec{A}|^2 would make no sense without the time-dependence being made clear. For example, with no time-dependence of A, there would be no electric field and this could be confusing to the non-expert.
Del Giudice, Fuchs and Vitiello: We agree with the referee also on this point. We have included in the text a sentence (see the paragraph after Eq. 1) clarifying that throughout the paper, space-time dependence of the variables is understood. Thus, when no misunderstanding arises, we omit writing them explicitly. When necessary we adopt the notation .
Vladimir Voeikov: Why do you look for a quantum explanation to the exclusion of the possibility of a classical one ?
Del Giudice, Fuchs and Vitiello: An essential step in the formation of the water bridge is the early appearance of vortices in the water, which are submitted to a high voltage. The result is a quantum feature that exists according to the general relationship coupling the electromagnetic potential to the space-time derivatives of the phase of the matter field. This relationship implies a wave-like energy transfer that does not fade with the distance. This implies a long-lasting adaptive tuning among the oscillations of molecules.
The motion of molecules in a classical framework would be diffusive and consequently would be quite random. The existence of coherence involving a large number of molecules is a quantum feature without a classical analogue.
Moreover, the ordered raising of large amounts of water—located at the origin of a stable water bridge—implies the appearance of levitating forces, such as those produced by the Meissner effect in superconductors. Classical mechanisms, such as those implied by field induced sprays of water, would hardly produce the formation of stable arches. That is due to the fact that classical mechanisms would demand a long-range attraction among the droplets of the sprayed water.
Voeikov: Could the dynamics of formation of the water bridge be also at work in the process of formation of living structures?
Del Giudice, Fuchs and Vitiello: This question could not be answered in a rigorous way at the present moment. However, in living organisms there are many examples of quasi one dimensional structures, dynamically built, which disappear at death. This is the point at which, presumably, the overall coherence of the system fades away. An example is given by the cell cytoskeleton, whose elements are made up of self-piped water coated by biomolecules resonating with the e.m. field trapped inside. A model of cytoskeleton incorporating such a feature is described in Del Giudice E., Doglia S., Milani M., Vitiello G., “A dynamical mechanism for cytoskeleton structures” in Interfacial Phenomena in Biological Systems (Ed. M. Bender) Marcel Dekker Inc, New York (1991), pag. 279-285. Del Giudice E., Doglia S., Milani M., Vitiello G., Electromagnetic field and spontaneous symmetry breaking in biological matter, Nucl. Phys. B275 [FS 17], 185 (1986).
In any case, this question needs much further investigation.
