Phloem Translocation of Organic Compounds: A Possible Mechanism to Assist Osmotically-Generated Pressure Flow in Tall Trees
Johnson RJ1* and Canny MJ2
1Independent researcher, Oxford, UK
2Plant Science Division, Research School of Biology, RN Robertson Building, The Australian National University, Canberra, ACT 0200, Australia
*Correspondence E-mail: bob.johnson1000@gmail.com
Key Words: phloem translocation, Münch osmotically-generated pressure flow, EZ layer, Coulomb repulsion, Canal Transport Model
Received September 12th, 2012; Accepted December 30th, 2012; Published January 5th, 2013; Available online January 15th, 2013
Abstract
A supplementary model of phloem translocation is postulated to work in tandem with the Münch osmotically-generated pressure flow (OGPF) model in order to reduce the high pressures required by the OGPF model for flows in tall trees. The supplementary model relies on the assumption that the known symport of protons during solute loading into the phloem is maintained during transport along the sieve-tube elements. Evidence is brought forward in support of each of the necessary components of the postulated Canal Transport Model. Contrary indicators are also discussed and experimental tests of the hypothesized model are suggested. It is hoped that the evidence presented may contribute to the ongoing debate about the pressure flow hypothesis.
Article Outline
- Introduction
- Summary
- Overview of the Hypothesised Model
- Conclusions
- Discussion with Reviewers
- References
Introduction
The preferred candidate mechanism for transport in the phloem vessels is osmotically generated pressure flow (OGPF), as originally proposed by Münch (1927). The flow is presumed to be governed by the Hagen-Poiseuille Equation, with the osmotic pressure given by the van t’Hoff relation.
The model can satisfactorily explain flows in smaller plants. However, as for example Turgeon (2010) has pointed out, it remains difficult to reconcile the OGPF theory with phloem transport in tall trees.
The principal problems relate to the pressures and energy requirements required by the Münch model to drive the flow through the narrow pores in the sieve plates which form barriers to the flow along the sieve tubes. As has been noted by various researchers, it is by no means certain that the high pressure required to drive flow in tall trees can be generated by the plant; the pressure gradients required by the theory have not been observed in practice; and the energy demands of Poiseuille flow through the narrow pores are extremely high.
Various alternative physical models have been suggested to date in attempts to overcome these well-known problems. These include turgor-driven mass flow in both the simple (Münch 1927) & modified forms; Cyclosis, or rotational protoplasmic streaming (Curtis 1929); Modified streaming (Mason & Phillis 1936); Surface spreading on fluid phase interfaces (van der Honert 1932); Electro-osmotic mass flow (Fensom 1957; Spanner 1958; Dainty Croghan & Fensom 1963); Accelerated diffusion by moving strands (Canny 1962; Canny & Phillips 1963); Cytoplasmic / peristaltic pumping (Thaine 1969; Aikman & Anderson 1971); Relay Models (Lang 1979; Aikman 1980; Murphy & Aikman 1989); and Osmoregulatory Flow (Thompson & Holbrook 2003a,b). In parallel with the physical models, various quantitative models of OGPF flow have been propounded, as discussed by Pickard in one of the more recent predictive analyses (Pickard 2012).
However, no alternative physical model has yet been preferred to the Münch model despite the known problems. As Froelich et al. stated: “The pressure flow hypothesis remains an issue of debate.” (Froelich et al 2011, p4442), a view echoed by Knoblauch & Oparka (2012): “Contrary to expectation, recent high-resolution non-invasive studies of the phloem have not provided unequivocal support for the Münch pressure-flow hypothesis. This is an uncomfortable situation given its widespread acceptance.”
Turgeon (2010) suggested two possibilities for resolving the problem. Either the data is incorrect due to unrecognized technical difficulties; or perhaps something fundamental is missing from the OGPF theory.
In this paper, we endeavor to put forward a new concept for the “missing” elements in the Münch model, to be considered alongside the other suggestions to date.
Requirements for the “Missing” Elements
As discussed above, the principal requirement of any new hypothesis is to avoid the very high pressures and consequent pressure gradients and energy demands imposed by the OGPF model of flow through the small sieve plate pores. These problems become more significant with transport distance, a point addressed by the relay models which attempt to “unitize” the mechanism and thereby break the dependence on distance. This is clearly an advantage.
Other factors should also be taken into account.The observed rate of specific mass transfer is proportional to the sucrose concentration gradient. (Canny 1973, pp36-39 & Fig. 3.2 ) Therefore any model should operate as an analogue of sucrose-related diffusion but with an enhanced diffusion coefficient.
Sucrose is by no means the only substance transported with the translocation stream (see e.g. Canny 1973, Ch.4). Lalonde et al. (2003) list the main osmotic concentrations of phloem sap as sugars, amino nitrogen compounds [amino acids] and potassium. Any model should preferably allow for the transport of the full range of solutes found in the phloem.
Additionally, there is some evidence, although it is disputed, that bi-directional flow may occur both in a single sieve tube and also, more surprisingly, in a single sieve tube element. (e.g. Eschrich 1967; Trip & Gorham 1968; Peterson & Currier 1969; Stock & Silvester 1994; see also Canny 1973, Ch.6). The modified OGPF model should offer the possibility of bi-directional transport of solutes, both simultaneously in the same sieve tube element, and in different directions within the stem of the plant in order to supply sinks higher than sources.
Before considering what type of model might satisfy these requirements, it is worth looking briefly at the source of the high pressure requirement in the Münch model.
The Role of Sieve Plates
As recognised by Mason, Maskell & Phillis in 1936 (quoted in Canny, 1973, p72), the principal problems with the Münch OGPF model relate to the presence of the sieve plates and the resistance they offer to mass flow.
The pore size in gymnosperms ranges from 0.05 – 0.8 μm (Canny 1973, p142) but calculations of available energy from the sugars consumed in the phloem preclude flow being driven through holes much finer than 0.6 μm diameter. (Canny 1973, p165). In other words, only the largest of the pores in gymnosperms are seemingly of any practical use in passing a pressure-driven flow.
Gymnosperms have sieve plates at approximately 1200 μm centers. (Canny 1973, p164) The subsequent evolution of the angiosperms, with sieve plates at approximately every 400 μm along the sieve tubes and pores with a typical mean diameter of ~2 μm (Esau & Cheadle, 1959, p159, Table 1) seems to suggest that there is an evolutionary advantage of the sieve plates despite the barrier they appear to present to Poiseuille flow.
An active role for the sieve plates has already been postulated by proponents of electro-osmotic models. Unfortunately, these models suffer from the problem that the total amount of energy required is at least as great than that required for pressure-driven mass flow. As Dainty et al. (1963) pointed out, the problem of the energy required to drive the flow is not solved simply by changing the driving mechanism. As they stated: “..the power used by electro-osmosis can never be less than that used by a pressure mechanism.” (Dainty et al. 1963, p963) Of course, that statement assumes that the same mass flow has to be driven through the pores in both cases.
Towards a Supplementary Model
Apart from Curtis’ original recirculatory protoplasmic streaming model, all the alternative models mentioned in the Introduction above share one common factor: all of the phloem sap is assumed to pass through the pores of the sieve plates.
An obvious solution to the problem of driving large volumes of fluid through small pores in sieve plates is that the plant does not do this. Recalling that the primary function of phloem translocation is the delivery of sucrose and other solutes to the demand sites, it is not necessary to achievement of the primary function to also transport the bulk of the solvent across the sieve plates.
Suppose, therefore, that only the solutes and a minimum amount of solvent are transported across the sieve plates.
An analogy could be made with a canal boat. A boat (e.g. a sucrose molecule) travels along the canal system (sieve tubes) but the water (solvent) in the canal stays in each section between locks (sieve plates); only a small amount of water is lost as the boat passes through a lock (the small amount of solvent passing through the pores with the sucrose). The boat arrives at its destination while the transport fluid remains largely stationary in the system.
Continuing the analogy, the boat needs to travel between the locks. In order for the solutes to traverse the length of each sieve tube in accordance with the observed transport rates, it will be necessary to have a mechanism for rapid transport along each tube, but one which does not involve the solvent flowing through the end plates.
A possible solution is to have a recirculatory flow within each sieve-tube element. This concept is similar to the view expressed by de Vries in 1885 and supported by Curtis in the 1920s (according to Canny 1973, p70).
Combining the above suggestions results in the concept of a Canal Transport Model of phloem translocation as a supplementary mechanism to OGPF flow which could help reduce the high pressure requirements.
Suggestions as to how such a model might be achieved in practice will be discussed below based on various strands of evidence, but first the nature of the cargo being transported must be investigated.
The Nature of the Sucralose Molecules
As mentioned above, the observed flow behaves as though the rate of diffusion of sucrose was in some way accelerated. Acceleration implies the presence of an additional force acting on the sucrose molecules causing them to separate more rapidly than would be expected from diffusional collisions alone.
One possibility is that the sucrose molecules are electrically charged and subject to Coulomb repulsion.
There appear to be a number of reasons why the sucrose molecule may carry a net positive charge:
a) Sap is known to be partially ionized. For example, Fensom states: “In plants the tissues may be thought of as membrane packets filled with liquid. These liquids are dilute electrolytes and in such solutions it is the ions which move appreciable distances, not electrons.” (Fensom 1959, p1004)
b) Sugar molecules are known to be strongly hydrated. The OH– groups in the sucrose molecule attract a cloud of polar water molecules which form hydrogen bonds with the hydroxyl groups. When sap is concentrated, it rapidly reduces the concentration of free water molecules, as evidenced by the curve of its osmotic pressure vs. concentration. Above about 1M (the frequent concentration in sieve tubes) the curve continues to rise steeply, in contrast to an Ideal Solution and to other solutes. Figure 1 below shows the significantly different behavior of sucrose in solution.
c) Due to the stronger Coulomb forces, H3O+ and any free H+ ions in the solvent may be expected to bond to the OH– groups on the sucrose in preference to neutral water molecules bonding to the same groups.
d) Experiments seem to indicate that sap does carry a net positive charge. Fensom & Spanner state that electrically-induced flow was always towards the cathode. (Fensom & Spanner 1969, p322)
e) Plants are known to carry a net positive charge above ground level; there is a potential gradient down the stem consistent with the sucrose carrying a positive charge. (Fensom 1963, Gensler 1974)
The evidence suggests that the sucrose molecules may attract a net positive charge of protons or hydronium ions while in solution in sap in the phloem in preference to attracting polar but neutral water molecules.
Possible additional evidence in support of the charged nature of the sucrose molecule can be found in Fensom’s work on electro-osmotic forces. Under an applied electric field, sucrose was transported across an otherwise sucrose-impermeable cell membrane in the same direction as K+ cations. (Fensom et al. 1967, p1272)
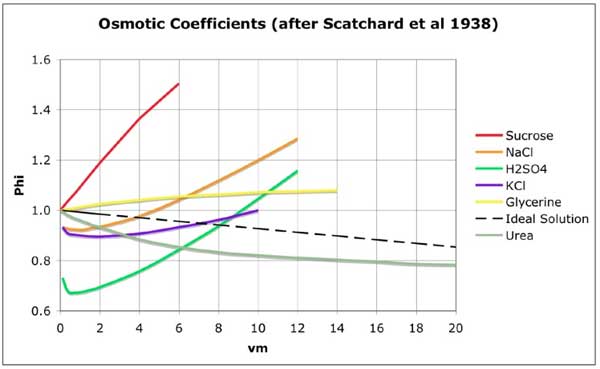
Figure 1: Graphs of Osmotic Coefficient φ as a function of Total Molality vm for various solutes. (after Scatchard, Hamer & Wood 1938, Fig. 2)
Whilst the author considered that this was due to viscous drag between neutral sugar molecules and the positive ions, it seems possible that the effect was due to forces acting directly on charged sucrose molecules themselves.
Evidence for symport of sucrose and protons has accumulated recently. For example, Lalonde et al. (2003) reported that:
“These features are satisfied by proton symporters that load se/cc complexes from the leaf apoplasm with sucrose (Riesmeier et al. 1993; Stadler et al. 1995; Truernit & Sauer 1995; Stadler & Sauer 1996; Kühn et al. 1997; Barker et al. 2000; Weise et al. 2000) or with mannitol (Noiraud et al. 2001).” (ibid p41 and references therein)
More recently, Zhou et al. (as reported in Geiger 2011) have proposed a six-state reaction cycle of the proton-coupled disaccharide carrier ZmSUT1 for sucrose loading across membranes in which the sucrose molecule is always transported with a proton through a sucrose/proton symporter. (Geiger 2011, Fig. 4, after Zhou et al. 1997) Geiger concludes that ZmSUT1 is working on the basis of a 1:1 H+ sucrose stoichiometry. (Geiger 2011, p398)
Might the proton in fact be bound to the OH– hydroxyl groups on the sucrose molecule in preference to hydration with water molecules?
The Nature of the Other Principal Solutes
It is well known that amino acids and potassium form significant proportions of the solute load of phloem sap e.g. Lalonde et al. 2003 state: “Source loading and sink unloading of sugars, amino N compounds and potassium largely account for phloem sap osmotic concentrations and hence pressure differences.” (ibid p37)
Interestingly, these authors found that amino acids are also loaded along with protons. “Amino acid loading into the phloem is also carried out by H+-coupled transport (Fischer et al. 1998; Ortiz-Lopez, Chang & Bush 2000; Delrot et al. 2001; Williams & Miller 2001).” and further report an “observed accumulation ratios of amino acids and sucrose (Lohaus et al. 1995) given a stoichiometry of 1 : 1 between solute and proton transported (Bush 1993).” (Lalonde et al. 2003, p41 and references therein)
This appears to be similar to the sucrose loading stoichiometry discussed above.
Weston et al. (1995) discuss the loading of particular amino acids into Ricinus communis L. roots and found “The transport of glutamine, isoleucine, glutamic acid and aspartic acid was driven by both a pH gradient and a membrane potential (internally alkaline and negative), created artificially across the plasma membrane. This is consistent with transport via a proton symport. In contrast, the transport of the basic amino acids, lysine and arginine, was driven by a negative internal membrane potential but not by a pH gradient, suggesting that these amino acids may be taken up via a voltage-driven uniport.” (ibid p166)
We can possibly explain these findings by noting that lysine and arginine are both known to have positively-charged side chains and hence would automatically be subject to electrical forces due to voltage gradients. In contrast, the remaining amino acids listed have either polar, hydrophobic or negative side chains and appear to require proton symport for loading towards the internally-negative side of the membrane.
As with the sucrose molecule, we hypothesize that the protons are in fact bound to, or at least always associated with, the amino acids during transport, causing the amino acids to behave as positively charged molecules. Similarly, it is well known that potassium forms a positive ion, K+ in solution.
We will proceed on the assumption that the main solutes i.e. sucrose molecules, amino acids and potassium, do all carry a net positive charge while being transported in the undamaged phloem.
The Canal Transport Model Hypothesis
There are four principal mechanisms required for the hypothesized Canal Transport Model to be able to transport the “cargo” of positively-charged solutes and satisfy the bi directional flow requirement in full:
a. An arrangement which allows for bi-directional flow in each sieve-tube element; &
b. A driving mechanism for “accelerated diffusion” of solutes within individual sieve-tube elements; &
c. A means of separation of solutes from the bulk flow at the sieve plates; &
d. A driving mechanism for the solutes through the sieve plates
Possible evidence for each of the above mechanisms are considered in turn.
a. An arrangement which allows for bi-directional flow in each sieve-tube element
One way in which bi-directional flow within a single sieve-tube element could be achieved is by separating the counter-flowing streams into an Annulus and a Core arrangement. If the solutes were concentrated within the core area of the lumen then the recirculation of the majority of the solvent could occur in a counter-flow in the annulus around the core. The Annulus and Core flow mechanism is examined in more detail below, but first a means of concentrating the solutes into the core area is also required.
Recent research by Pollack and his co-workers (Pollack 2003; Zheng & Pollack 2003, 2006) may provide the necessary mechanism. They have demonstrated that water in contact with a hydrophilic surface develops a negatively-charged structured water layer adjacent to the surface. This structured layer actively excludes solutes. Pollack therefore terms the structured water layer an “Exclusion Zone” or “EZ layer.”
Klyuzhin et al. (2008) have demonstrated a similar concentration effect with colloidal particles in suspension in hydrophilic tubes. As the cytoplasmic lining of the sieve-tube elements is also hydrophilic, formation of an annular negatively-charged EZ layer adjacent to the lining could be expected. The positively-charged solutes would then be concentrated into the core region of the lumen of the sieve-tube element.
It might be objected that the positive and negative layers could not exist side by side without recombining but there is evidence that this need not necessarily be the case. It is known that a charge separation between adjacent layers can be maintained in water despite the Coulomb forces between the layers. In addition to Pollack and co-worker’s research mentioned above, Klimov & Pollack’s (2007) experiments demonstrated formation and maintenance of a similar double layer in an experimental chamber. They state:
“… perhaps the most interesting finding is that in solutions of pure water with dye, two distinct zones exist with different charge carriers: one with an excess of H+, H3O+, or larger positively charged clusters of “pure water”; the other with an excess of OH- or larger negatively charged clusters. With pH < 4 and pH ≈ 10 in the respective zones, the ratio of charge carriers is more than one million. Hence, different charge carriers carry current in the respective zones.” (Klimov & Pollack 2007, p11893)
We must point out that some studies using fluorescent dyes in the living phloem appear to show the dyes evenly distributed throughout the entire sieve tube, which would be counter to the proposed separation into annulus and core. See for example Knoblauch & van Bel (1998). Certainly this is a potential problem for the recirculatory part of the model. However, various points should be borne in mind when viewing fluorescent dyes in the sieve tubes.
Firstly, the dyes themselves may affect the behavior of the system; they cannot necessarily be considered to be non-involved indicators, as Fuchs demonstrated in different circumstances. (Fuchs 2010 p399) Indeed, Knoblauch & van Bel (1998) themselves found that introducing RH-160 into living sieve-tube elements appeared to lead to a thick layer of parietal protein being deposited onto the sieve plates after an hour (ibid Fig 4F), suggestive perhaps of a minor damage response.
Secondly, although Pollack and colleagues (references as above) demonstrated that all the solutes tested in their experiments were excluded by the EZ layer, it should be verified in laboratory experiments based on Pollack’s model that the exclusion principle also applies to the fluorescent dyes used in the phloem experiments before reaching firm conclusions based on the use of these dyes.
Thirdly, the optical lensing effects of the system when viewed in longitudinal profile may themselves distort the picture such that the dyes merely appear to occupy the whole lumen whereas they may not actually do so. Transmitted light and fluorescence emanating from inside the sieve-tube will necessarily be scattered by the non-planar geometry of the liquid and surroundings.
And lastly, the effect of illuminating the system during the experiment cannot necessarily be discounted. As Knoblauch & van Bel (1998) found, laser illumination itself caused a damage-like reaction and the authors warned against the use of unlimited laser radiation for the study of living cells (ibid p47). In the current context involving postulated charge-separated layers in the sieve-tube elements, the effect of photo-ionization induced by the experimental illumination could prove deleterious to the hypothesized Canal Transport Model.
Nevertheless, if the dyes are subject to exclusion by hydrophilic surfaces and do indeed demonstrate uniform distribution throughout the undisturbed and unaffected lumen then the recirculatory feature of the proposed model would be in doubt. However, the principle of reduced solvent transmission through the pores would not be affected if it is also found that the solutes do not exert significant drag on the solvent molecules and so are able to move relatively independently of the bulk solvent. (See section b. below).
If, however, these contra-indications to an Annulus and Core arrangement can be resolved then the EZ layer mechanism may offer the possibility of explaining bi directional flow as a type of recirculatory mechanism.
b. A driving mechanism for “accelerated diffusion” of solutes within individual sieve-tube elements
To recap, the postulated arrangement in each sieve-tube element is as follows: all the solutes are assumed to act as positively-charged molecules. The solutes may be concentrated into a core region which is surrounded by an Exclusion Zone annulus formed adjacent to the sides of the lumen.
This would result in the core region having a net positive charge while the EZ layer may retain its usual negative charge. If the total charge in the two zones is numerically equal then the sap will be charge-neutral overall.
Figure 2 below is provided for reference and visualization of the concept. Note that the relative cross-sectional areas of the annulus and core will depend on the thickness of the Exclusion Zone, the percentage of solvent passing through the sieve-plate pores with the solutes, and the velocities of flow in the annulus and core themselves, none of which can be determined theoretically and may in fact be variables depending on the solute concentration. Nevertheless, as a first approximation it is reasonable to suppose that the cross-sectional areas of the EZ annulus and the core are of a similar size.
If we ignore for the moment any components of the OGPF and recall that the observed flow rate is apparently dependent on the sucrose concentration gradient, let us consider what happens when sucrose is delivered via a sieve plate at the upper end, say, of a sieve-tube element.
Due to the increased sucrose concentration at the upper end, a charge gradient will develop along the core of the element which will start to drive the charged sucrose molecules along the core by Coulomb repulsion. The other positively-charged solutes will also contribute to the net force. Each positively-charged molecule will drag a number of neutral water molecules with it in a manner similar to electro-osmotic flow (Fensom & Dainty 1963, p689; Fensom et al. 1965, p453). As an indication of the order of magnitude of the expected effect, when electric fields were applied to an excised vascular strand from the petiole of the water plant Nymphoides peltatum, Fensom & Spanner estimated the efficiency of viscous forces as 100 water molecules per ion (Fensom & Spanner 1969, p328).
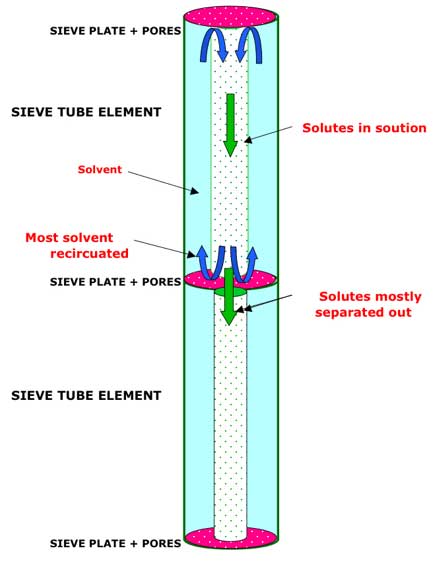
A: Annulus and Core flow in two consecutive sieve-tube elements.
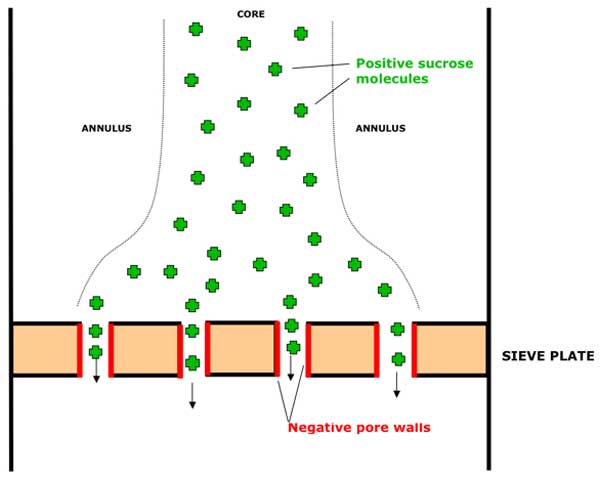
B: Solutes approaching sieve plates.
Under the postulated Canal Transport Model, most of the solvent (water) does not pass through the sieve plate at the lower end of the element and so any downward movement of the core region will start a recirculatory flow whereby most of the solvent returns up the element via the annulus. If, however, the viscous forces between the solutes and the water molecules is insufficient to drive the whole core at the same velocity as the solute molecules then the recirculatory element of the flow will be minimized.
In either situation, the net effect is that each sieve-tube element is provided with an efficient and rapid means of transporting sucrose and other solutes from the end with higher concentration to the end with lower initial concentration. Non-OGPF flow will cease in an element when there is no sucrose concentration gradient within that element.
Under this mechanism, non-OGPF flow may occur in each element independently of flow in other elements. Flow in any one element is only dependent on the solute concentration gradient in that element. This implies that the flow is “unitized” in the same manner as the relay model hypotheses, and therefore the flow becomes largely independent of the transport distance.
A key requirement of any model is to demonstrate transport proportional to the sucrose concentration, analogous to but faster than normal diffusion. In the current model, this will occur automatically due to the charge on the sucrose molecules which form the largest proportion of the solutes. The effect of the Coulomb repulsion forces between each positively charged molecule will ensure that they ‘diffuse’ apart much more rapidly than expected by simply collision-based diffusion. Bearing in mind that the observed diffusion rate is equivalent to that expected in a gas with the same sucrose concentration (Canny 1973 p37), the strong electrical forces would appear to be ideally suited to meet this requirement. The magnitude of the electrical forces involved can be appreciated in the case of semi-permeable membranes where the pressure induced by the concentration gradient can be balanced by a small Nernst potential.
Apparently contra the hypothesised model, Froelich et al. (2011) found occasional agglomerations of P-protein across the lumen; these agglomerations may contain one or more open “channels” of ~0.5 – 1 micron diameter, aligned in the direction of flow and free of filaments. It might be thought that these agglomerations dictate against the proposed model by blocking the core region, and against the Münch hypothesis for a similar reason. However, the agglomerations appear to be irrelevant to both models given the apparently high porosity of the whole agglomeration and the lack of any significant effect on transport velocity. (Froelich et al. 2011, p442)
c. A means of separation of sucrose from the bulk flow at the sieve plates
Sieve plates comprise layers of cell wall, membrane and associated cytoplasm from two consecutive sieve-tube elements which together close the ends of each sieve-tube element. Small pores penetrate each sieve plate and may in total amount to some 50% of the area of the plate. Some pores may be partially blocked by a fibrillar strand of P protein (Froelich et al. 2011).
We may expect that the hydrophilic lining of the pores will generate a negatively-charged EZ layer as discussed above in relation to the sieve-tube elements. This negatively charged layer will create a negative electric potential in the pore. If the pore is unobstructed then the electric potential in the core zone of an EZ-lined pore through a thin sieve plate is given approximately by: (1) V ≈ Q–/K r (after Spanner 1952, p390) where Q– = total negative charge in the EZ layer; K = dielectric constant for water in bulk; & r = pore core radius.
For a given total charge, the potential varies inversely with pore radius; on the other hand, for a given surface charge density in the EZ layer the potential will be independent of the pore radius.
The positively-charge solute molecules will be drawn into the zone of negative potential in the pore preferentially to any uncharged water molecules and so the solute molecules will automatically tend to be separated from the majority of the solvent in the sieve tube. (See Figure 2b above).
From Equation (1) above, it can be seen that small pores will be at least as effective as large pores in generating a negative potential and hence in separating out the solutes. This may help to explain the function of the small pores in the gymnosperms.
The presence of any hydrophilic filaments in the pores, as found by Froelich et al. (2011) in a minority of pores, could likewise increase the negative potential in the pore and therefore could enhance the separation of sucrose into the remaining space between the filament and the sides of the pore.
d. A driving mechanism for the sucrose molecules through the sieve plates
The above section demonstrated how solutes could be separated from the bulk solvent and drawn into the sieve-plates pores. We now consider how the solutes may then be driven through the pores into the next sieve-tube element.
If there is a concentration gradient across any one sieve plate due to the arrival of solute along the upstream element, the charge concentration gradient along the pore will automatically drive the positively-charged sucrose molecules downstream through the pore channel towards the region of lower charge in the downstream element in a manner similar to the postulated flow in a sieve-tube element as discussed above. The pores may act as small versions of the sieve-tube elements, being subject to a similar Annulus and Core arrangement and driving forces.
Any EZ lining in the pores may cause an effect similar to that found by Spanner (1952):
“… the diffusion rates of positive ions are likely to be much higher (perhaps enormously so) through the pores of a negatively charged membrane.” (Spanner 1952, p390).
An Annulus and Core arrangement in the pore suggests that there may be a simultaneous return flow of water through each pore which could balance the volume lost to a sieve-tube element by solute flow across each sieve plate in cases where the flow volume was not being replenished by OGPF along the whole sieve tube. Once again, in the absence of OGPF, supplementary flow according to the postulated model could occur in any pair of elements independently of flow in the other elements in the same sieve tube, thereby maintaining the “unitized” nature of the Canal Transport Model.
In contrast to the electro-osmotic flow models, there is no need to maintain a constant, unidirectional and independently-generated potential drop across all the sieve plates in the flow path. The charged solutes generate the potential difference required for their own transport across the sieve plates and the unitized nature of the flow mechanism does not require the same potential across every sieve plate.
When considered together with the flow along the sieve-tube elements discussed above, it can be seen that the flow of solutes in the plant stem may be in either direction at any one time depending only on the relative sugar concentration between consecutive sieve-tube elements. Abstraction by a demand sink, or addition of sugar from a supply source, will change the concentration in sieve-tube elements and across sieve plates local to the sink or source, which will automatically trigger a balancing flow from the elements upstream or downstream. The “common header” model of each sieve tube shown in Canny Fig. 5.2 (Canny 1973, p65) will be maintained automatically.
Summary
The postulated Canal Transport Model is intended as a supplement to the Münch OGPF model in tall trees. The key features of the model can be summarized as follows:
- The hydroxyl groups on sucrose molecules are hypothesized to be hydrated preferentially with hydronium ions or bound to free protons, resulting in a net positive charge on each sucrose molecule. Evidence for sucrose/proton trans-membrane symport suggests that the association may be maintained in the phloem.
- Amino acids in the phloem likewise either demonstrate proton symport or have naturally positively charged side chains. Potassium forms a positive ion. The main solutes therefore seem to demonstrate a tendency to behave as positively-charged molecules or ions.
- Solutes may be concentrated into the core region of the phloem lumen by the formation of annular Exclusion Zones or EZ layers, as found by Pollack and his co-workers (see references above).
- Flow in any one sieve-tube element may take the form of a core flow of concentrated solutes and a return flow of bulk solvent in an annulus around the core.
- Accelerated diffusion occurs due to Coulomb forces between the positively-charged solutes in the core region, or throughout the whole lumen if the Annulus and Core arrangement and recirculation are not significant.
- The electrical driving force is proportional to the solute concentration gradient; neutral water may be dragged by viscous forces as seen in electro-osmotic flow. The apparent diffusion rate of solutes will be higher than simple diffusion, as observed.
- Only the solutes and a small amount of solvent are transported across sieve plates between adjacent sieve-tube elements; the high pressure and energy requirements of driving mass flow of large amounts of solvent through the pores is avoided.
- The non-OGPF flow of sucrose between consecutive sieve-tube elements is only dependent on the concentration gradient across the sieve plate between them; sugar transport may therefore be simultaneously upwards and down-wards in the stem from an zone of high concentration, in accordance with Canny’s “common header” model.
- Bi-directional flows of solvent could occur within any one sieve-tube element via the annulus and core arrangement, if this exists.
- The flow is largely independent of distance because the driving force along a sieve-tube element and across a sieve plate is the sucrose concentration gradient within each sieve-tube element and between consecutive elements respectively.
- Flow in each sieve-tube element and across each sieve plate may take place independently of the flows in other elements and across other sieve plates; consecutive elements will respond in turn as the sucrose gradient reaches them and triggers flow in that element.
- Each sieve-tube element effectively acts as a stand-alone unit which reacts to the sugar concentration in that element.
- As the plant grows in height, new elements can be added to the system without compounding the flow problem.
- Sieve plates allow this mechanism to function efficiently and locally within the plant by dividing the sieve-tube into short elements. They also limit the mass flow of solvent. More frequent sieve plates allow finer control of abstraction by sinks. This may explain the evolutionary advantage of sieve plates.
Overview of the Hypothesized Model
The Canal Transport Model hypothesis was suggested by the idea that the OGPF driving pressures in tall trees could be reduced if the sieve plate pores only allowed solutes and a minimum of solvent to pass, whilst the bulk of the solvent was retained in the upstream sieve-tube element. This mechanism could also allow bi-directional transport in one sieve tube. Adding the possible requirement for bi-directional flow in one sieve-tube element led to the concept of recirculatory flow. We then explored what mechanisms would be required to allow this model to operate. We found that there is a certain amount of experimental evidence for mechanisms which could support the hypothesis, although it has to be admitted that there may be some counter-evidence as well, which we have highlighted.
Whilst the Authors accept that the arrangement of the various strands of evidence into the hypothesized Canal Transport Model is somewhat speculative, the only new assumption is that the hydroxyl groups on the sucrose molecules attract hydronium ions or protons preferentially to neutral water molecules, and that the amino acids are likewise associated with protons during transport in the phloem, as has been demonstrated by others to occur in relation to loading and unloading of these solutes into the phloem channel.
The remainder of the model follows from this assumption when considered in relation to recent demonstrations of the creation of Exclusion Zones of negatively-charged water adjacent to hydrophilic surfaces, and the well-known electrical Coulomb repulsion forces between like charges.
If the annulus and core arrangement is not supported by experimental evidence, the recirculatory flow element which allows bi-directional flow in one sieve-tube element would be in doubt but the basic model with limited solvent passage through the sieve plates may still be valid.
Conclusions and Forward Look
We have attempted to reconcile the Münch osmotically-generated pressure model with various anomalous observations of phloem translocation in tall trees by the addition of a hypothesized “missing” mechanism which could work in tandem with the OGPF flow.
The postulated Canal Transport Model results in significantly reduced pressures, pressure gradients and energy demands for phloem translocation. It would operate as an analogue of accelerated diffusion and would be largely independent of distance as it allows new units to be added without significant penalty. The new model could also offer a mechanism for bi-directional transport both in a single sieve tube and in a single sieve-tube element which may be relevant if stronger evidence for these disputed aspects of the flow emerges in the future.
Experimental verification of the various propositions, and especially the presence of positive charge on the sucrose molecules and amino acids whilst in transit in undisturbed sap in the phloem, is obviously of vital importance in testing this hypothesis. Also, as a helpful reviewer of an earlier draft of this paper pointed out, the possible separation of sap into a solute-bearing core and an EZ layer annulus could be tested by direct comparison of axial isofluxes in solvent and solute, e.g. 18O and 13C, following isotopic labelling in a leaf.
The postulated Canal Transport Model supplement to the Münch model is offered for critical analysis and evaluation alongside the various alternative models already in the field. We hope that at least some of the ideas and evidence presented may be of interest in the ongoing discussion of the long-standing puzzles of OGPF-driven phloem translocation in tall trees and may lead to a renewed interest in the possible role of electrical forces in the process.
References
Aikman D, 1980. Contractile proteins and hypotheses concerning their role in phloem transport. Canadian Journal of Botany, 58: 826–832
Aikman DP, Anderson WP, 1971. A quantitative investigation of a peristaltic model for phloem translocation. Annals of Botany, NS, 35: 761-772
Canny MJ, 1962. The mechanism of translocation. Annals of Botany, NS, 25: 152-167
Canny MJ, 1973. Phloem translocation. Cambridge University Press, London, ISBN 0 521 20047 4
Canny MJ, Phillips OM. 1963. Quantitive aspects of a theory of translocation. Annals of Botany, NS, 27: 379-402
Curtis OF, 1929. Studies on Solute translocation in plants. Experiments indicating that translocation is dependent on the activity of living cells. American Journal of Botany 39: 573-585
Dainty J, Croghan PC, Fensom DS, 1963. Electro-Osmosis, with Some Applications to Plant Physiology. Canadian Journal of Botany, 1963, 41(6): 953-966
Esau K, Cheadle VI, 1959. Size Of Pores And Their Contents In Sieve Elements Of Dicotyledons. Proceedings of the National Academy of Sciences, 45: 156-162
Eschrich W, 1967. Bidirektionelle Translokation in Siebröhren. Planta, 73(1): 37-49
Fensom DS, 1957. The bio-electric potentials of plants and their functional significance: I. An electrokinetic theory of transport. Canadian Journal of Botany, 35(4): 573-582
Fensom DS, 1959. The Bio-Electric Potentials of Plants and Their Functional Significance: III. The Production of Continuous Potentials Across Membranes in Plant Tissue by the Circulation of the Hydrogen Ion. Canadian Journal of Botany, 37(5): 1003-1026
Fensom DS, 1963. The bio-electric potentials of plants and their functional significance: V. Some daily and seasonal changes in the electrical potential and resistance of living trees. Canadian Journal of Botany, 41(6): 831-851
Fensom DS, Dainy J, 1963. Electro-Osmosis in Nitella. Canadian Journal of Botany, 41(5): 685-691
Fensom DS, Spanner DC, 1969. Electro-osmotic and biopotential measurements on phloem strands of Nymphoides. Planta, 88(4): 321-331
Fensom DS, Meylan S, Pilet P-E, 1965. Induced Electro-Osmosis in Root Tissues. Canadian Journal of Botany, 43(4): 453-467
Fensom DS, Ursino DJ, Nelson CD, 1967. Determination Of Relative Pore Size In Living Membranes Of Nitella By The Techniques Of Electroosmosis And Radioactive Tracers Canadian Journal of Botany, 1967, 45(8): 1267-1275
Froelich DR, Mullendore DL, Jensen KH, Ross-Elliott TJ, Anstead JA, Thompson GA, Pélissier HC, Knoblauch M, 2011. Phloem Ultrastructure and Pressure Flow: Sieve-Element-Occlusion-Related Agglomerations Do Not Affect Translocation. The Plant Cell, 23: 4428-4445.
Fuchs EC, 2010. Can a Century Old Experiment Reveal Hidden Properties of Water? Water Journal, 2: 381-410
Geiger D, 2011. Plant Sucrose Transporters from a Biophysical Point of View. Molecular Plant, 4(3): 395–406
Gensler W, 1974. Bioelectric potentials and their relation to growth in higher plants. Annals of the New York Academy of Sciences, 238: 280-299
Klimov A, Pollack GH, 2007. Visualization of Charge-Carrier Propagation in Water. Langmuir, 2007, 23: 11890-11895
Klyuzhin I, Symonds A, Magula J, Pollack GH, 2008. A new method of water purification based on the particle-exclusion phenomenon. Environmental Science and Technology 42(16): 6160-6166
Knoblauch M, van Bel AJE, 1998. Sieve Tubes in Action. The Plant Cell, 10: 35–50
Knoblauch M, Oparka K, 2012. The structure of the phloem – still more questions than answers. The Plant Journal, 70:147–156
Lalonde S, Tegeder M, Throne-Holst M, Frommer WB, Patrick JW, 2003. Phloem loading and unloading of sugars and amino acids. Plant, Cell & Environment, 26(1): 37–56
Lang A, 1979. A relay mechanism for phloem translocation. Annals of Botany (Lond.), 44: 141–145
Mason TG, Phillis E, 1936. Further Studies on Transport in the Cotton Plant. V. Oxygen Supply and the Activation of Diffusion. Annals of Botany os-50(3): 455-499
Münch E, 1927. Versuche über den Saftkreislauf. Ber. Dtsch. Bot. Ges., 45: 340–356
Murphy R, Aikman DP, 1989. An Investigation of the Relay Hypothesis of Phloem Transport in Ricinus communis L.. Journal of Experimental Botany 40(10): 1079-1088
Peterson CA, Currier HB, 1969. An Investigation of Bidirectional Translocation in the Phloem. Physiologia Plantarum, 22(6): 1238–1250
Pickard WF, 2012. Münch without tears: a steady-state Münch-like model of phloem so simplified that it requires only algebra to predict the speed of translocation. Functional Plant Biology, 39: 531–537
Pollack GH, 2003.The role of aqueous interfaces in the cell. Adv. Colloid and Interface Sci., 103(2): 173-196
Scatchard G, Hamer WJ, Wood SE, 1938. Isotonic Solutions. I. The Chemical Potential of Water in Aqueous Solutions of Sodium Chloride, Potassium Chloride, Sulfuric Acid, Sucrose, Urea and Glycerol at 25°. J. Am. Chem. Soc., 60(12): 3061–3070
Spanner DC, 1952. The Suction Potential of Plant Cells and Some Related Topics. Annals of Botany, ns XVI(63): 380-407
Spanner DC, 1958. The Translocation of Sugar in Sieve tubes. Journal of Experimental Botany, 9:332-342
Stock PA, Silvester WB, 1994. Phloem transport of recently-fixed nitrogen in the Gunnera-Nostoc symbiosis. New Phytologist, 126: 259-266
Thaine R, 1969. Movement of sugars through plants by cytoplasmic pumping. Nature, London 222: 873-875
Thompson MV, Holbrook NM, 2003a. Scaling phloem transport: Water potential equilibrium and osmoregulatory flow. Plant, Cell and Environment 26: 1561–1577
Thompson MV, Holbrook NM, 2003b. Application of a Single-solute Non-steady-state Phloem Model to the Study of Long-distance Assimilate Transport. J. Theor. Biol., 220: 419–455.
Trip P, Gorham PR, 1968. Bidirectional Translocation of Sugars in Sieve Tubes of Squash Plants. Plant Physiology, 43: 877-889
Turgeon R, 2010. The Puzzle of Phloem Pressure. Plant Physiology, 154: 578–581
van der Honert TH, 1932. On the mechanism of transport of organic materials in plants. Proc. Sect. Sci. K. ned. Acad. Wet., 35: 1104-1111
Weston K, Hall JL, Williams LE, 1995. Characterisation of amino-acid transport in Ricinus communis roots using isolated membrane vesicles. Planta 196, 166–174
Zheng J-m, Pollack GH, 2003. Long range forces extending from polymer surfaces. Phys. Rev. E 68: 031408 -1 to 7
Zheng J-m, Pollack GH, 2006. Solute exclusion and potential distribution near hydrophilic surfaces. ‘Water and the Cell’, Ed. Pollack GH, Cameron IL, Wheatley DN, Springer: Dordrecht, The Netherlands, 2006; pp165-174
Discussion with Reviewers
Anonymous Reviewer: This relationship of flow to concentration gradient occurs for OGPF too. So it is misleading to talk of a diffusion of sucrose, since there is a flow of both water and sugar (MRI data: Mullendore et al. 2010; Peuke et al. 2006; Windt et al. 2006; ).
R. Johnson and M. Canny: We accept that there is flow of both water and sugar. The use of the word “diffusion” is taken from the quoted literature. The paragraph in question makes it clear that the actual process is an analogue of diffusion, not diffusion per se. This distinction is maintained throughout the paper.
Reviewer: The enigma of sieve plates: the small pore diameter could have been evolved to protect the system from damage. The existence of stationary material in sieve elements remains a similar enigma, with flow unimpeded (now demonstrated by Froelich et al.).
Johnson and Canny: If the smaller pores of angiosperms had evolved in order to enhance the level of damage protection compared to the gymnosperms, it is still necessary to explain the significant additional energy cost imposed by smaller pores under the OGPF model. Whilst it is not unreasonable to allow that plants may have traded some additional energy for increased damage protection, angiosperms seem to have taken this to the point where the plant is barely able to cope with normal operation. As Turgeon stated: “The analysis above leaves the impression that trees live at the extreme edge of transport capability, with phloem transport motivated by a barely sufficient driving force.” (Turgeon 2010 p579)The suggested model overcomes this difficulty by reducing the energy demand; the plant may then be able to afford the additional damage protection more easily.
We discuss the enigma of Froelich et al.’s findings elsewhere in the paper.
Reviewer: The evidence for bidirectional flow remains is equivocal now as it was in 1971 (MacRobbie). It was seen only for a very low flow, not the situation foreseen for this proposal which is to provide an extra mechanism if OGPF/Münch is inadequate. So it is premature to propose an exclusion zone and re-circulating flow merely to allow bi-directionality; first, better evidence is needed.
Johnson and Canny: We accept that the evidence to date for bi-directional flow remains equivocal, as the paper makes clear. Nevertheless, we hope that mentioning the possibility of an explanation at this stage may stimulate research into whether the arrangement does or does not exist in the phloem and so help to settle the bi-directional flow debate one way or the other.
Reviewer: Some experiments to test the ideas need to be suggested. The isotope experiment is to test bidirectional flow, not the main hypothesis.
Johnson and Canny: One of the most important factors which we refer to in the Conclusions and Forward Look is that the sap must be undisturbed. This obviously imposes considerable constraints on any experimental verification of the postulated model. Nevertheless, application of small electric fields to living trees in order to determine the effect, if any, on the sap flow may be possible.
For example, if two aphids were identified to be feeding on the same sieve tube and both were excised from their stylets, a comparison could be made between the flow from one stylet to which a small potential had been applied and the other which was left to flow without further changes. If the sucrose molecules in the phloem are associated with positive charges, as hypothesized, then some differences should be expected.
Reviewer: A major conundrum is that I cannot understand the key proposal, that solute, carrying positive charge, is somehow propelled through sieve plate pores – (CTM Hypothesis, section D) “If there is a concentration gradient across any one sieve plate due to the arrival of solute along the upstream element, the charge concentration gradient along the pore will automatically drive the positively-charged sucrose molecules downstream through the pore channel..”. And further along in the same section: “The charged solutes generate the potential difference required for their own transport across the sieve plates..”. Yet, at the same time, (CTM Hypothesis, section B) “.. sucrose is delivered via a sieve plate, a charge gradient .. will .. drive the charged sucrose molecules .. by Coulomb repulsion.” Taken together, (and with the 10th bullet point in the Summary), these pore and element processes sound like perpetual motion, there is no source of energy. This suggests a major problem with the text, so that I am not getting the point. Is the OGPF intended to be an initiating force?
Johnson and Canny: The reviewer seems to have got the impression that the action of the sucrose concentration in different parts of the sieve tube amounts to perpetual motion. This would of course be impossible! The essence of the proposed model is that equalization of sucrose concentration occurs all along the sieve tube pathway, as would be expected if the “diffusion” was chemically driven. However, we suggest that the sucrose molecules receive an additional diffusion-like force from Coulomb repulsion between the protons or hydronium molecules associated with the sucrose molecules.
The situation is then analagous to equalization of electric charge along a wire in an electrical circuit. The “battery” is represented by the energy input at the phloem loading stage when new sucrose has to be loaded against both the chemical gradient and an electric gradient. This requires more energy than is required under the OGPF model to “prime” the system, but the resulting selective passage of sucrose through the sieve-plate pores leads to a reduction in the amount of bulk water passing through the pores. This saves more energy in the translocation process than was needed to prime the system. The overall process is therefore more energy-efficient than the OGPF model alone.
