 Why Is Catalase So Fast? Part 2: Schemes for Rapid, Exo-enzymatic Disproportionation of Hydrogen Peroxide
Why Is Catalase So Fast? Part 2: Schemes for Rapid, Exo-enzymatic Disproportionation of Hydrogen Peroxide
Lionel R Milgrom
17, Skardu Road, London NW2 3ES, UK
Correspondence E-mail: milgromlr27412@gmail.com
Keywords: Catalase; exo-enzymatic oxo-reductive hydrogen peroxide disproportionation; hydrogen-bonded networks; QED water coherent domains; Grotthuss mechanism
Received: January 17, 2018; Revised: May 1, 2018; Accepted: May 8, 2018; Published: June 26, 2018; Available Online: June 26, 2018
Abstract
Grotthuss-like proton transfer in and between QED-type water coherent domains, could partially explain how catalase might accomplish ultra-fast exo-enzymatic “unzipping” (disproportionation) of aqueous H2O2-containing cytoplasmic networks, to oxygen and water.
Introduction
The by-products of aerobic metabolism consist of a range of reactive oxygen species (ROS), most notably hydrogen peroxide (H2O2). This is broken down by catalase enzymes, without which aerobic existence would be impossible, if not deadly.
With large specificity constants kcat/Km of around 108 to 109 M-1 s-1 [Web ref. 1], catalases are capable of disproportionating many tens of millions of H2O2 molecules per second. In conventional terms, such catalytic perfection (Knowles and Albery, 1977) requires the enzyme to catalyze a reaction every time an H2O2 molecule collides with it. In order to achieve such extraordinarily high rates of reactivity however, H2O2 molecules would first have to diffuse randomly and extremely rapidly from the intracellular fluid, deep into the catalase active sites.
Haemin-containing catalases have four Fe(III) protoporphyrin IX complexes as active sites buried within the enzymes’ protein structures, and relatively far removed from the bulk intracellular aqueous milieu in which these enzymes function. This might suggest that catalases operate impossibly faster than H2O2 diffusion rates.
Such an idea would seem to contradict much of accepted enzyme kinetic theory developed over the last century [Henri, 1902; Deichmann, et al, 2013]. Advances in mathematical biology however question the validity of applying simplistic rate laws derived from well-stirred in vitro experiments, to how these enzymes actually perform in their much more crowded (and realistic) in vivo intracellular environments (Grima and Schnell; 2006). It is difficult therefore, to fully reconcile the speed, precision, and subtlety of catalases with a classical reductionist narrative of diffusion-controlled random molecular collisions.
An alternative hypothesis for catalase efficiency has recently been proposed [Milgrom, 2016]. In it, each catalase enzyme molecule acts as a “hub” embedded in, connected to, and acting upon, an essentially exo-enzymatic hydrogen-bonded network of intracellular water and H2O2 molecules. Oxo-reductive “pulses” (originating from decomposition of two H2O2 molecules within each of the enzyme active sites) are then rapidly transmitted to and through this extended H-bonded network, causing the rest of the exo-enzymatic H2O2 molecules to in effect, “unzip.”
However, the plausibility of this network reaction scenario rests on generating a scheme in which H2O2 molecules could feasibly break down to water and oxygen outside the enzyme. In this paper, it is suggested Grotthuss-like proton transfer [Web ref 4] between water “coherent domains” [Klein, 2006; Ho, 2012; Del Giudice, 2015], might provide such a scheme.
1 The specificity constant (or kinetic efficiency) is used as a measure of the efficiency of an enzyme because the rate of reaction varies directly with how frequently enzyme and substrate meet, and how efficiently they bind.
2 Having said that, it is known the rates of some enzyme-catalyzed reactions do exceed the diffusion-controlled limit, e.g., those enzymes in organised assemblies inside cell membranes [Web ref 1].
About Catalase
The overall decomposition of H2O2 by catalase is given as:
2H2O2 = 2H2O + O2 [Eq 1]
In conventional biochemistry, the accepted mechanism for this decomposition envisages a two-step oxo-reductive process shown in equations 2 and 3 [Alfonso-Prieto, 2008], where “Enz-[Por-Fe(III)]” represents the resting state of the enzyme and its Fe3+ porphyrin active site, respectively. The latter undergoes two-electron oxidation and oxygen transfer via an H2O2 molecule (itself reduced to water) to an oxyferryl porphyrin π-cation radical, represented by “Enz-[Por+.-Fe(IV)=O]” in equation 2.
The ≠-cation radical is then reduced back to its resting state by a second H2O2 molecule [Diaz, 2012], which is itself oxidized to water and oxygen in equation 3. Combined, these reactions simplify to the oxo-reductive reaction shown in equation 1. [Boon et al, 2007]
Enz-[Por-Fe(III)] + H2O2 = Enz-[Por+.-Fe(IV)=O] + H2O [Eq 2]
Enz-[Por+.-Fe(IV)=O] + H2O2 = Enz-[Por-Fe(III)] + H2O + O2 [Eq 3]
Adding Eq 2 and 3 2H2O2 = 2H2O + O2 [Eq 1]
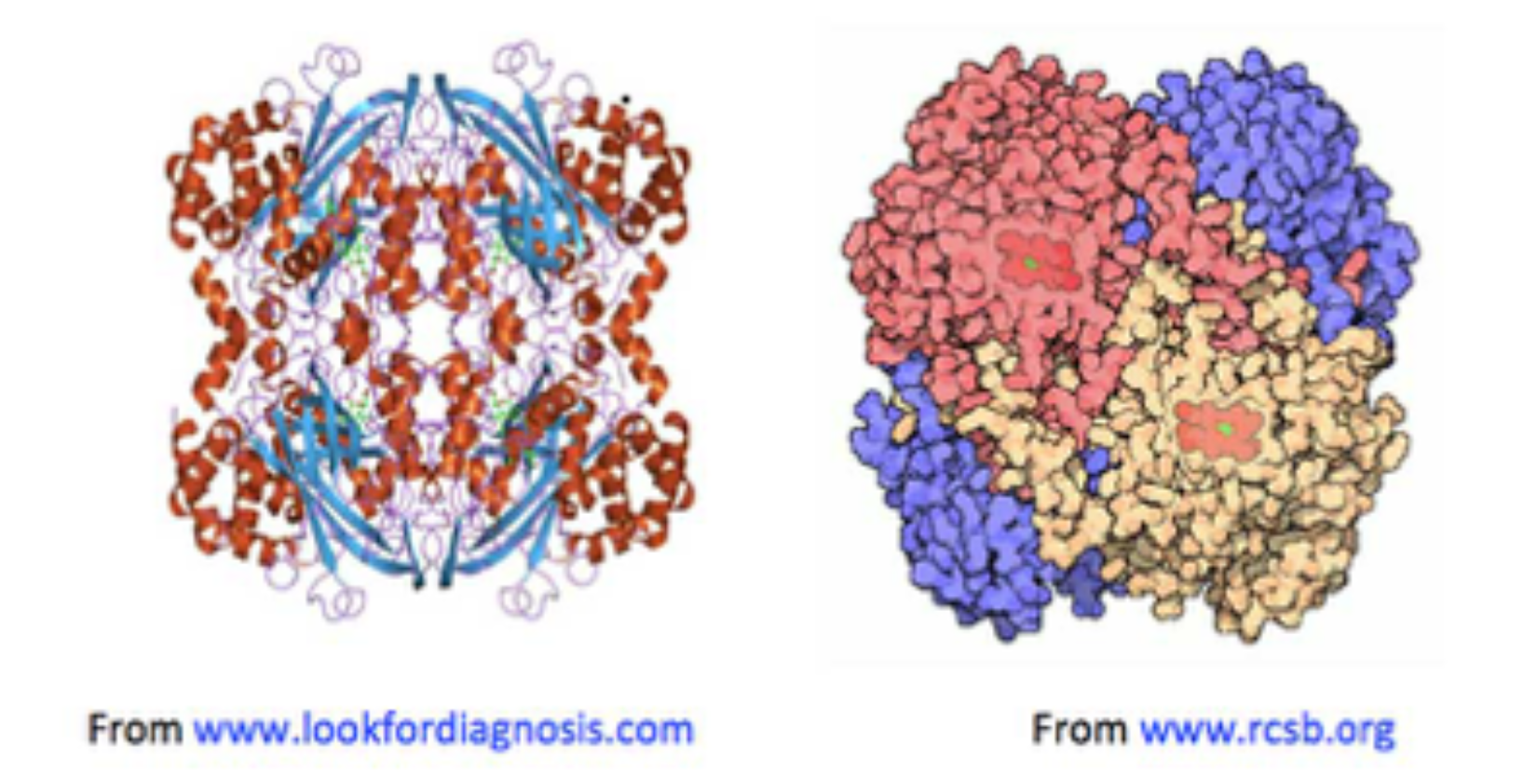
Figure 1. Two images of catalase, both showing haemin units (on the left, in green: on the right in red), buried below the surface of the enzyme, along increasingly narrow channels, lined with hydrophobic amino acids.
The requirement for two molecules of H2O2 is supposed to ensure that the first-formed highly active oxyferryl porphyrin π-cation radical intermediate does not survive long enough to cause inactivation and oxidative degradation of the enzyme.
Previously [Milgrom, 2016], it was noted how detailed analyses of catalase crystal structures [Murthy, 1981; Reid, 1981; Vainshtein, 1981; Foroughi, 2011], combined with molecular dynamics studies had revealed:
• Haemin-containing catalases consist of four tightly integrated sub-units with active sites buried inside each sub-unit around 2 nm beneath the catalase molecular surface;
• Channels lead from the catalase surface down into the enzyme’s active sites: the main ones are about 4-4.5 nm in length [Dominguez, 2010; Kalko, 2001];
• Amino acids with strongly H-bonding side-chains (e.g., histidine, proline and charged residues) line the catalase surface and channels, so that the relative proportion of H2O2 to water molecules is thought to increase gradually, from the bulk phase around the enzyme, to close to its surface (about 0.4-0.5 nm away), into the channels.
Therefore, catalase enzyme amino acid sequences appear to have evolved so that in an intracellular environment containing it, H2O2 gradually concentrates at the active sites, accounting for these enzymes’ catalytic efficiency [Dominguez, 2010]. Such a conclusion would seem to support the widely held assumption that the catalase disproportionation reaction occurs via an ultra-rapid but essentially sequential progression of individual H2O2 molecules through the enzyme’s active sites. Could there be another possibility?
In aqueous solutions, H2O2 forms hydrogen bonds with water. Earlier results from Raman spectroscopy had indicated these might be slightly weaker than those formed between water molecules themselves [Giguère, 1984]). In addition, compared to 100% H2O2, a recent ab initio quantum mechanical charge field molecular dynamics simulation of aqueous H2O2 suggested such H-bonding is indeed strong enough to ensure hydrogen peroxide’s stabilization in water [Moin, et al., 2012]. Consequently, within the aqueous environment of an aerobic organism’s intracellular fluid, H2O2 could conceivably form a network of dynamically hydrogen-bonded molecules [Web ref. 2].
In addition, there is experimental evidence that the decomposition of H2O2 is accelerated above phospholipid membrane surfaces, and this has been successfully modeled [Solis-Calero et al., 2011]. Catalase enzymes therefore would be sitting within (and via their active sites, connected to) this hydrogen-bonded network.
Finally, recent quantum electrodynamics (QED) calculations indicate water forms large coherent domains consisting of many water molecules [Klein, 2006; Ho, 2012; Del Giudice, 2015]. The possibility arises that synergistic interactions between catalase, the cytoplasmic semi-aqueous medium containing H2O2 embedded in and around water coherent domains, and cellular phospholipid membranes might well lead to the ultra-fast disproportionation of H2O2 outside the enzyme.
Enzyme Action: Result of Random Collisions or Coherent Control/ “Action at a Distance”?
The energetics of in vivo bio-molecular processes were discussed in the previous paper [Milgrom, 2016]. It concluded the classical reductionist view [Dawkins, 1988] was inadequate [Watterson, 1991] when considering bio-molecular structure and function within the cellular cytoplasm. This is because the amount of energy liberated by bio-molecular processes, e.g., substrate binding to an enzyme, can be shown to be easily more than enough to disrupt the all-important hydrogen-bonded 3-D structure [Fersht, 1999] of an enzyme each time it functions [Kauzmann, 1959; Tanford, 1968].
That as catalysts, enzymes survive and are reused suggests this energy is effectively dissipated. Certainly the aqueous cytoplasmic medium must be involved, but when considering interactions between biomolecules, and biomolecules and their substrates, do they always have to be in direct contact? “Through-space” interactions should be included.
Indeed, several interactions have been invoked recently to explain ultra-fast enzymic behavior. These include “action-at-a-distance” spacial and force-field factors between enzyme and substrate [Chou and Jiang, 1974], and quantum mechanical tunnelling [Garcia-Viloca et al., 2004; Kurian, 2014; Olsen et al., 2004; Pusuluk et al., 2017]).
Implicit in these interactions is the notion of dynamic self-organization and integration of cellular bio-molecular processes, involving intimate and active participation of the intracellular aqueous environment. Such an outlook would be of far greater relevance to a holistic understanding of biochemistry than current preoccupations with individual biomolecules and their structure/function relationships occurring within an essentially inert aqueous solvent background. This is particularly so when considering bio-molecular processes involving ROS [Voeikov, 2001].
Thus, “ROS are traditionally regarded in the biochemical literature as highly hazardous particles [Fridovich, 1998]…blamed as…the reason for many diseases, and as a major cause of ageing [Ames et al, 1993]…” [Voeikov, 2001]. Certainly radicals (except for peroxide, O22-, ROS consist of radicals, e.g., superoxide, O2-. and hydroxyl radicals, OH.), and chain reactions involving them, damage important biological molecules under in vitro conditions.
However, in vivo the situation is much more subtle. Many organisms use one-electron reduction of oxygen to generate ROS, specifically not only in immune reactions (e.g., via the enzyme NADP-H-oxidase) to kill bacteria and viruses [Jones et al, 1996], but also for intra- and extra-cellular signalling [Khan & Wilson, 1995; Saran et al, 1998; Gamalay & Klybin, 1999]. Indeed, up to 10-15% of oxygen consumed by an organism at rest is converted into ROS. This figure increases when the organism is under stress. Oxygen both generates and quenches free radicals (Figure 2), (bio)photons being emitted in the process [Voeikov, 2001].
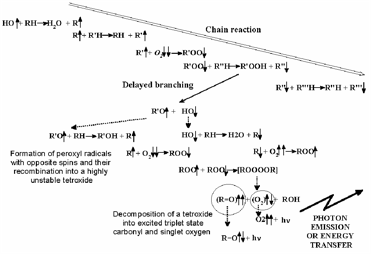
Figure 2. Outline of chain branching reaction (from Voeikov, 2001): peroxy compounds are formed.
It appears that far from being the “bad boys” of biology, ROS are vital for normal functioning of organisms. Consequently, perhaps the role of antioxidant enzymes, e.g., superoxide dismutase (SOD) and catalase, and their relationship with the semi-aqueous cellular environment in which they operate, needs to be reassessed. Before that, however, some considerations about the intracellular aqueous environment require mentioning.
3 At physiological pH, superoxide is more likely to exist as the neutral hydroperoxy radical HO2. [de Grey, 2002]
Coherent Water and Cooperativity
Water’s many highly anomalous properties have been well documented [Chaplin, 2018a; Gallo, et al., 2016; Ho, 2012], and are describable in terms of quantum electrodynamics (QED) [Del Giudice et al., 2015]. Thus, quantum fluctuations and coupling between matter and electromagnetic fields in QED predict quantum coherence for liquid water under ordinary temperatures and pressures. This is thought to lead to the formation of large, stable, “coherent domains”about 100 nm in diameter and consisting of many millions of water molecules.
Quantum chemical computations [Klein, 2006] indicate that such coherent domains involve the formation of hydrogen-bonded supramolecular clusters, leading to cooperativity, i.e., the tendency of individual chemical interactions to influence each other, so that local actions can have global effects and vice versa [Cooperative and Coherent Water, 2010]. The cooperativity of such supramolecular water clusters is indicated by a progressive shortening of hydrogen bond lengths and an increase in their electron density and bond strength (see Figure 3).
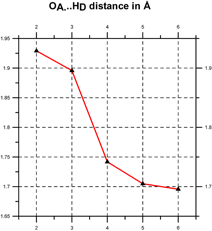
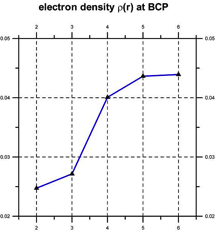
Figure 3. Cooperativity shortens (left) and strengthens the hydrogen bonds (right) [after Klein, 2006].
In this formalism, water may be thought of as existing as a two-phase system in which one of the phases is coherent, i.e., all the water molecules are correlated. The other phase consists of individual molecules in an uncorrelated gas-like state [Del Giudice et al, 2015].
The QED concept of coherent domains can also help explain the phenomenon of “Exclusion Zone water” (called EZ water because it excludes solutes, [Del Giudice et al., 2015]) that occurs when water is in contact with hydrophilic surfaces, e.g., large biomolecules such as proteins [Pollack, 2013: Zheng et al., 2006]. Such EZ water has greater viscosity and is electrically charged similar to the surface in which it is contact, which accounts for its solute-excluding properties.

Figure 4. Schematic of an aqueous system near a negatively-charged surface [from Del Giudice et al., 2015].
The coherence of such EZ domains exists over ranges of many microns, resulting in potential differences large enough to ionize water molecules. Thus, water in contact with a positively-charged hydrophilic surface will have an interfacial EZ enriched with positive charges, and a bulk phase with an excess of negative charges. This order is reversed in the case of water in contact with a negatively charged hydrophilic surface (Figure 3). The phenomenon of EZ water and its effects on cellular reactions is something the classical reductionist view is unable to predict or explain.
4 Watterson’s “wave-cluster-domain model” attempts to integrate the active cooperation and participation of cellular water with the action of a cell’s biomolecular components [Watterson, 1991; Watson, 1995]
A Network Hypothesis for Catalase Action
Previously [Milgrom, 2016], it was mentioned percolation theory had been used to model giant hydrogen-bonded water clusters [Geiger et al. 1979; Partay et al. 2007]. This is relevant to the argument to be developed here because if the aqueous cellular cytoplasm is in a state above the percolation threshold, then (as predicted by QED [Klein, 2006; Ho, 2012; Del Giudice, 2015]) a coherent, cooperative global hydrogen-bonded network might be assumed to exist within it. That hydrogen peroxide is also able to form strong hydrogen bonds with water [Moin, 2012] gives added impetus to the notion that catalases might operate within an intracellular hydrogen-bonded coherent co-operative network. We shall return to this.
The catalase enzyme is now envisaged as a “hub” sitting in a hydrogen-bonded network of water coherent domains and H2O2 molecules that are connected via the channels leading from the enzyme’s surface, to its active sites. This means instead of considering the H2O2 molecules as being presented individually and in rapid succession to the active sites, it is necessary to consider the whole network of nH2O2 molecules hydrogen bonded to water coherent domains and each other, spreading out and away from the enzyme.
As before in equations 1-3, the enzyme’s resting state is represented by Enz-[Por-Fe(III)], and the active state oxo-ferryl cation radical as Enz-[Por+.-Fe(IV)=O]. The H2O2 molecule closest to the active site oxidizes the resting enzyme to its active state, and is itself reduced to water. However, this leaves (n-1)H2O2 molecules still networked.
The active state of the enzyme then oxidizes an H2O2 molecule to water and oxygen but being connected to the rest of the H-bonded network, causes the latter to effectively ‘unzip’ other H2O2 molecules, the whole network undergoing a fast coherent reaction to water and oxygen. The sequence of reactions may be formulated as follows:
Enz-[Por-Fe(III)] + nH2O2 = Enz-[Por+.-Fe(IV)=O] + H2O + (n-1)H2O2 [Eq 6]
Enz-[Por+.-Fe(IV)=O] + (n-1)H2O2 = Enz-[Por-Fe(III)] + H2O + O2 + (n-2)H2O + (n-2/2)O2 [Eq 7]
Adding 6 and 7 gives
nH2O2 = 2H2O + O2 + (n-2)H2O + (n-2/2)O2 [Eq 8]
which simplifies to
nH2O2 = nH2O + n/2O2 [Eq 9]
Doubling both sides of equation 9 and dividing through by n, gives finally equation 1
2H2O2 = 2H2O + O2 [Eq 1]
By effectively reproducing equation 1, this series of equations imply the preliminary network hypothesis does not contradict known catalase H2O2-disproportionation oxo-reductive chemistry. However, what has previously been lacking is a detailed scheme by which such an exo-enzymatic “unzipping” might take place.
5 Percolation theory defines a percolation threshold below which formation of long-range connectivity in random systems cannot exist [Sorge A, 2015; Stauffer, 1985]
Possible Scheme(s) for Exo-enzymic Catalase-Induced H2O2 Disproportionation
In 1804, Theodore von Grotthuss proposed a hopping mechanism for proton (H+) transport via transfer of positive charge between water molecules, involving exchange of a hydrogen bond with a covalent bond between H and O atoms [Miyake et al 2016]. The simplest way to indicate this is:
![]()
This implies movement of electrons in the opposite direction to proton transfer (see Figure 5). More sophisticated versions of such “hopping” may be envisaged (e.g., involving proton migration via H-bonded water clusters [Web ref. 4], see Figure 5), but it is in this regard that the Grotthuss mechanism (and versions of it) might be considered one of the possible agents for coherent cooperative behavior in water.
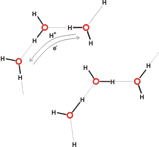
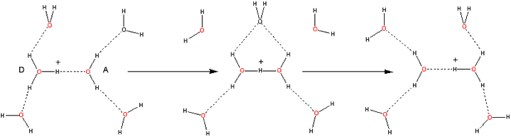
Figure 5 A (top left). Grotthuss mechanism of proton transfer in aqueous solutions; B (above). Proton transfer via hydroxonium ions (see the website, http://www1.lsbu.ac.uk/water/grotthuss.html)
Taking into account what has been mentioned previously concerning coherent water, cooperativity, and the pH altering effects of EZ layers next to hydrophilic surfaces, it appears reasonable that a variation on the Grotthuss scheme could be part of a useful basis for describing how exo-enzymatic H2O2 decomposition might occur.
Thus, in Figure 6, we see how, starting with the oxo-reductive pulse from the catalase active site (involving hydride {H–} transfer from a H2O2 molecule to the ferryl oxygen atom), the resulting proton transfer between hydrogen bonded H2O2 molecules could lead to exo-enzymic decomposition to oxygen and water.
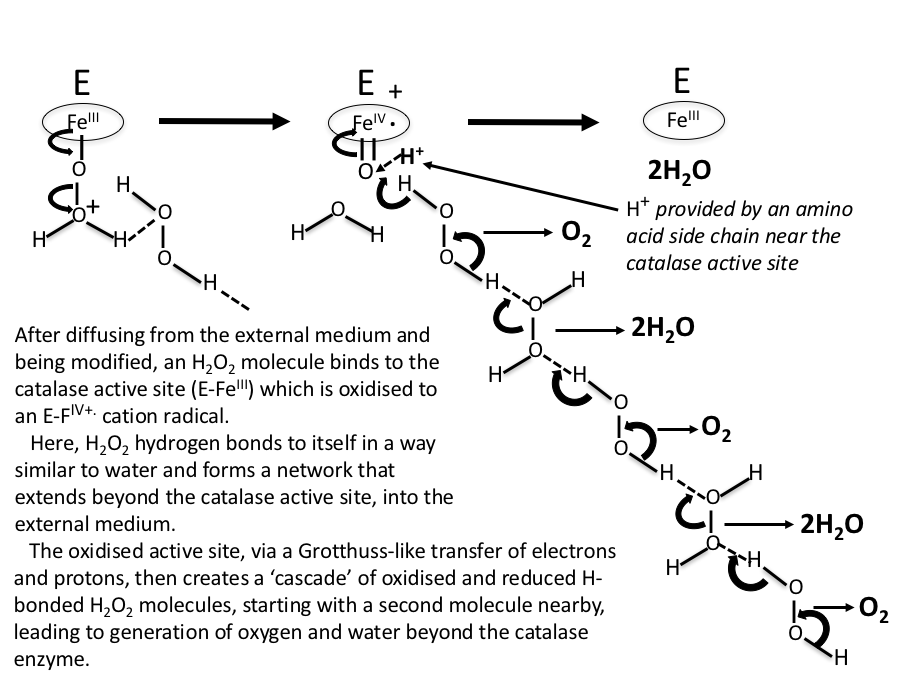
Figure 6. How an oxo-reductive pulse from catalase reaction centers could “unzip” H-bonded H2O2 molecules.
In this scheme, no account is taken of any water molecules that might eventually be H-bonded between H2O2 moieties. In Figure 7, water molecules are included in the H2O2 decomposition pathway. Again, this is initiated by an oxo-reductive pulse from the catalase active site (involving H– transfer from a H2O2 molecule to the ferryl oxygen atom).
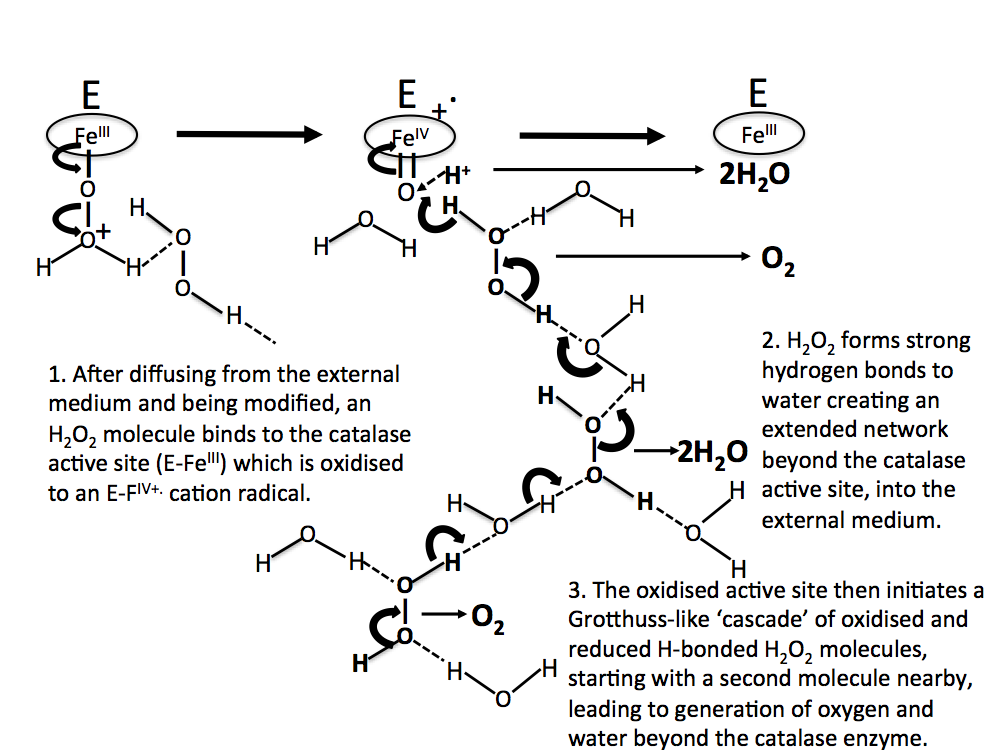
Figure 7. As in Figure 6, but with water molecules H-bonded between H2O2 moieties.
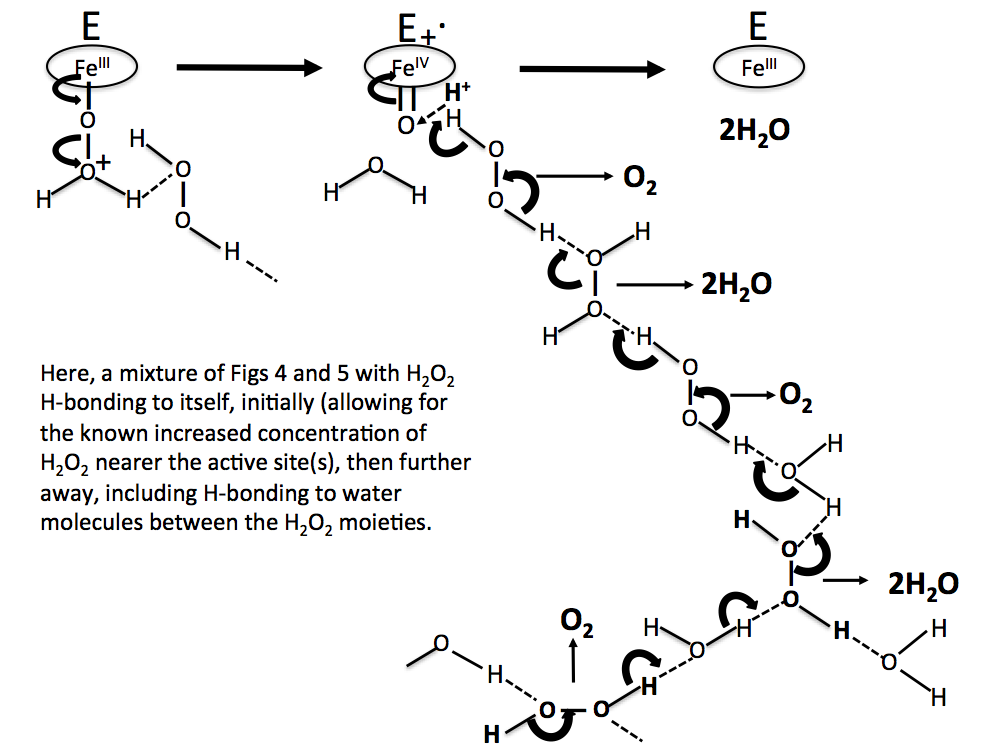
Figure 8. A more realistic sequence than Figs 6 and 7, with H2O2 molecules concentrated near the reaction site, and water molecules H-bonded between H2O2 molecules further away.
Such Grotthuss-like proton-hopping schemes admittedly by themselves have more in common with the precepts of in vitro reductionist solution chemistry: they take no account of what other possible effects might also originate from the enzyme interacting with the intracellular semi-aqueous environment.
As has been mentioned, the quantum electrodynamic (QED) treatment of water predicts a two-phase system, consisting of some water molecules in an essentially gaseous random state, while the remainder form into large coherent domains [Klein, 2006; Ho, 2012; Del Giudice, 2015]. These consist of giant stable clusters of many water molecules all resonating together (i.e., entangled), essentially receiving and transmitting molecular “information.” Could the gradual production of intra-cellular H2O2 and its possible H-bonded insertion into these coherent domains lead to them becoming increasingly destabilized (e.g., raising their energy by interfering with the H-bonded water structure holding the coherent domains together)? If so, then above a certain H2O2 concentration, might the collapse of these domains release that energy, sparking a Grotthuss-like exo-enzymatic decomposition of H2O2 that reforms the coherent domains? In other words, is this H2O2 decomposition QED led, Grotthuss-like proton hopping led, or are they different representations of the same phenomenon?
Discussion
The idea of exo-enzymatic activity [Milgrom, 2016] is not in itself new. Before the now familiar lock-and-key [Stryer et al,. 2002] and induced fit models [Koshland, 1958], early ideas of enzyme action imagined they induced changes in the surrounding aqueous medium, which then accelerated reactions in molecules nearby [Kohler, 1973].
Interestingly, the late Alexander Rothen proposed a similar idea to explain the results of his experiments with Formvar membrane-protected immobilized trypsin: enzymic action on the substrate was observed even though the trypsin did not cross the membrane [Rothen, 1979; 1982]. More recently, a similar notion (involving coherent “action-at-a-distance”) has been suggested to explain the enzymic action of endonucleases when reading DNA sequences [Kurian, 2014].
Consequently, we should expect such exo-enzymatic activity not to be confined merely to those enzymes that happen to have large specificity constants: it should be a more general phenomenon observable in other enzymes. This is because many enzyme systems have surface amino acids that are hydrophilic polar/charged. In the case of catalase, this helps concentrate H2O2 molecules near and into the channels leading to the enzyme’s active sites [Dominguez, 2010]. But as Pollack has pointed out, these are also the conditions that could generate exclusion zone (EZ) layers near the enzyme’s surface [Pollack, 2013; Zheng et al., 2006]. In addition, EZ layer formation leads to the generation of protons (as hydroxonium ions), and less frequently, solvated hydroxide ions.
Again, in the case of catalase, protons in the presence of transition metal ions such as Fe(II)/Fe(III), are known to provide catalytic environments for H2O2 redox chemistry [Goldstein et al., 1993; Web ref. 5]. Consequently, and in the words of Pollack, “…biological catalysis may resemble generic catalysis, involving little more than high concentrations of EZ-generated protons.”
Therefore, given that according to equations 6-9 and 1 the network hypothesis presented here and previously does not appear to violate known chemistry and biochemistry, the notion that catalase activity during H2O2 disproportionation might also be occurring in the cytoplasmic aqueous medium seems reasonable, if plausible schemes can be envisaged. The purpose of this paper has been to provide one such type of scheme, shown in Figures 6-8.
However, what Figures 6-8 do not show is the possible role of water coherent domains in such exo-enzymatic oxo-reductive schemes. If, as mentioned above, fluctuating metabolic H2O2 production leads to destabilization of water coherent domains, then their collapse would probably release energy, resulting in fluctuating electromagnetic fields and involving the emission of biophotons, as mentioned by Voeikov [Del Giudice et al., 2015]. In addition, such energy release could lead conceivably to the exo-enzymatic Grotthuss-like oxo-reductive schemes shown in Figures 6-8. The combination of QED and Grotthuss-like effects seems like a plausible scheme for the following reasons:
• It is reasonable to expect catalase breakdown of H2O2 to occur via a non-radical mechanism, in order to avoid massive over-production of hydroxy radicals e.g., via Fenton-type chemistry [Barbusinski, 2009].
• Exo-enzymatic breakdown of H2O2 by catalase would provide a reservoir of ground-state triplet oxygen in the intracellular aqueous medium, capable of interacting with the branching chain reaction, as advanced by Voeikov [Voeikov, 2001].
• The oxo-reductive decomposition of H2O2 (equation 1) generates around 98 kJ/mole of energy [Cotton et al., 1995], which if released rapidly inside the enzyme, even sequentially, could denature and therefore inactivate it [Kauzmann, 1959; Tanford, 1968; Fersht, 1999; Finney, 1982].
• Recent work involving single-molecule fluorescence correlation spectroscopy [Riedel et al., 2015] suggests the heat released during enzyme catalysis generates an asymmetric pressure wave that results in differential stress at the protein-solvent interface which transiently displaces the center of mass of the enzyme.
• Coherent domains within water are stabilized via H-bonding. If however H2O2 becomes “doped” into these coherent domains, it is possible the domains’ stability is compromised via introduction of H-bonding “defects” into their overall dynamic quasi/liquid crystalline structure.
• Combined with the effect of the asymmetric pressure wave at the protein-solvent interface mentioned earlier, an approximately 2 eV [Voeikov, 2001] oxo-reductive pulse originating from a catalase active site via decomposition of two H2O2 molecules (or a coordinated 7-8 eV pulse from all four active sites via decomposition of eight H2O2 molecules), might provide enough activation energy to trigger reformation of coherent domains, via exo-enzymatic decomposition of H2O2 into oxygen and water, the latter being incorporated back into the domain structure.
• Finally, as previously mentioned, the decomposition of H2O2 is also accelerated near phospholipid membrane surfaces [Solis-Calero et al., 2011].
Putting all these elements together, it is possible to envisage a process by which catalase might catalyze the exo-enzymatic decomposition of H2O2:
1. There is build-up of intracellular H2O2, generated by cellular metabolism.
2. This “dopes” aqueous intracellular coherent domains, causing “defects” in their H-bonded quasi/liquid crystalline dynamic structure, effectively destabilizing them.
3. H2O2 molecules in the catalase active sites are oxo-reductively decomposed.
4. This creates an energetic “pulse” that is rapidly transmitted exo-enzymically via Grotthuss-like proton hopping through the H-bonded water-H2O2 network, where it “rebounds” off phospholipid membranes.
5. The net result is in essence a molecular “whiplash” with rapid decomposition of H2O2, from both catalase and phospholipid ends of the “whiplash,” that releases water, oxygen, and energy exo-enzymically.
6. This effectively allows the coherent domains’ dynamic structure to re-stabilize.
7. The released water becomes part of the regenerated coherent domains, while the oxygen produced might conceivably serve as a reservoir controlling branching chain reactions (see Figure 2) that produce radicals.
8. The above steps repeat themselves as again, intracellular H2O2 begins to build up.
Conclusion
It could be argued that there is an intellectual “disconnect” between two parts of this scheme, i.e. the Grotthuss-like hydrogen-bonded exo-enzymatic mechanism of oxo-reductive intracellular H2O2 disproportionation, and the QED coherent domain view of two-phase water. Could this disconnect be viewed as a “clash of cultures”?
The chemical sciences (biochemistry included) are rooted in a classical view of molecules as geometrically structured atomic aggregates, occupying 3-D space and separately interacting with each other via direct contact. Quantum physics on the other hand, adopts a more sophisticated holistic approach: entities interact through fields “at a distance,” via superposition of their overlapping multi-dimensional wave functions, leading to their coherence and entanglement (recently shown to be two sides of the same coin [Levi et al., 2014; Streltsov et al., 2015]).
Because the generally accepted scientific paradigm tends to be local, reductionist, and causal, it consists of a set of assumptions about reality that not only have difficulty accommodating holistic structures and relationships, they are not geared towards incorporating non-local (acausal) correlations, e.g., coherence and entanglement.
The apparent “culture clash” arises because although the chemical sciences have for some time been imbued with quantum theory, classical ideas of molecular structure still remain. It has been described as a “felt need,” aided and abetted by the Born-Oppenheimer approximation that adiabatically separates electronic and nuclear motion [Wooley, 1978]. Without this separation it is usually argued [e.g., Atkins, 1999], calculations on the quantum states of molecules or understanding their properties, would not be possible (that this is not actually the case is a separate issue [Sukumar, 2009; Dalton et al., 1980]).
But classical ideas of molecular structure long predate quantum theory. In reality, what the Born-Oppenheimer approximation does is to give those ideas a kind of quantum legitimacy: without it, quantum theory has little to say about what most in the chemical sciences would regard as molecular structure. It has to be said however, that for most of the time and for the practical purposes of most chemical scientists, this is not a problem.
Nevertheless, a molecular structureless QED approach would probably require the construction of a wavefunction or wavefunctions encapsulating all the coherent cellular chemical and biochemical “actors,” e.g., proteins, DNA, lipids, water, salts, etc, etc. Assuming this could be done, though it might indeed have great predictive power, the question remains whether such a task would result in anything tangible or meaningful to chemical scientists.
A better solution might be to move away from the classical “ball and stick” viewpoint of molecules (which in any case, is inconsistent with quantum theory) and realize that in itself, a quantum state is not a physical property but instead reflects our state of knowledge about observable aspects of “reality” [Cyranski, 1985; Zeilinger, 2004]. Consequently, one could envisage a wavefunction encapsulating all coherent cellular chemical and biochemical “actors,” collapsing upon observation. Applied to molecules and biomolecules, such a view permits structure to arise and exist only when this is compatible with the observable evidence.
Although the study of water structure is far from easy [Chaplin, 2018b], recent work using ultrafast 2D infra-red anisotropy of water provides evidence that H-bond connectivity switches through concerted motions of water molecules, involving large angle molecular reorientation [Ramasesha et al., 2011]. This might suggest a Grotthus-like H-bonded switching mechanism could indeed be part of a scheme for exo-enzymatic oxo-reductive intracellular H2O2 disproportionation. However, this would have to be viewed (indeed, might only be possible) within an overall context provided by QED water coherent domains. Perhaps for the time being at least, this resolves the disconnect/”culture clash” mentioned above.
In conclusion, bearing in mind the importance of ROS to the normal functioning of any organism, the role of SOD and catalase would seem to be more about policing and controlling ROS, rather than ensuring their total obliteration from any aerobic organism.
Also, a re-evaluation of the role of the cytoplasmic aqueous medium (on enzyme activity in particular, and cellular biochemistry in general) is required, not just in stabilizing the structures of proteins and other biomolecules but playing an active and important role in their function and in the overall processes that maintain life [Voeikov, 2001]. If so, such a re-evaluation might ultimately be considered as important to biochemistry as quantum theory and relativity have been to physics.
For example, the physicist John Wheeler once described General Relativity with the deceptively simple dialectic, “Space-time tells matter how to move; matter tells space-time how to curve.” [Wheeler, 2000]. Is it possible that at the microscopic level, water might be as important to biomolecules as space-time is to matter in relativity theory?
This is no fanciful comparison as analogies between space-time and water have been noted previously, e.g., gravitational bending and trapping of light around and within a black hole [Haller et al., 2013; Karrasch et al., 2015] and the illumination of and trapping of light within a water vortex (the illuminated vortex produces a shadow on the bottom of a vessel that has all the hallmarks of a black hole [Barr et al, 2016]. This analogy becomes even more compelling when it is realised strong mathematical similarities exist between Einstein’s field equations and the Navier-Stokes equations of fluid dynamics [Bredberg et al., 2011; Bredberg, 2012; Rodriguez et al., 2012].
As analogies go, however, these might be considered to be operating at the macroscopic level. What the discussion in this paper could be suggesting is that a similar space-time/water analogy might exist at the nanoscopic level, i.e., that of water and biomolecules.
In emphasising the importance of water in biology, the Hungarian Nobel Laureate and biochemist Albert Szent-Györgyi used the powerful metaphor, “Water is the mater and matrix; mother and medium. There is no life without water.” [Collins, 2000].
An expression as concise as Wheeler’s for space-time and matter might help delineate a similar (but this time, molecular) dialectic [Imyanitov, 2016] between water and biomolecules. Given the previous discussion concerning active cooperation between the aqueous cytoplasmic medium and cellular biomolecules, Szent-Györgyi’s metaphor might be reformulated as:
“Water tells biomolecules how to fold; biomolecules tell water how to bind.”
Much more experimental and theoretical “water under the bridge” (i.e., work) will need to be performed however, before such a laconic formulation can be said to truly reflect the relationship between a cell’s internal aqueous environment and the biomolecules it contains.
6 I thank a referee for pointing this out.
References
Alfonso-Prieto M, Vidossich P, Rodriguez-Fortea A, Carpena X, Fita I, Loewen P, Rovira C (2008). Electronic state of the molecular oxygen released by catalase. J Phys Chem 112: 12842-12848.
Ames BN, Shigenaga MK, Hagen TM (1993). Oxidants, Antioxidants, and Degenerative Diseases of Aging. Proc Nat Acad Sci USA 90: 7915-7922.
Atkins PW (1999). Physical Chemistry 6th Edition, Oxford University Press, Oxford, UK, 1999.
Barbusinski K. (2009). Fenton Reaction – Controversy concerning the chemistry. Ecological Chemistry and Engineering vol 16 no 3 pp 347–358.
Barr I A, Bull A, O’Brien E, Drillsma-Milgrom K A and Milgrom L R (2016) Illuminating black holes Phys Educ 51 043001.
Boon EM, Downs A, Marcey D. Proposed Mechanism of Catalase. Catalase: H2O2: H2O Oxidoreductase: Catalase Structural Tutorial. Retrieved 11/02/2007.
Bredberg I, Kepler C, Lysol W, Strominger A (2011). From Navier-Stokes to Einstein. ArXiv:1101.2451v2 [hep-th].
Bredberg I (2012). The Einstein and the Navier-Stokes Equations: Connecting the Two. Doctoral Dissertation. Harvard University.
Chaplin M (2018a). Anomalous properties of water in Water Structure and Science.
Chaplin M (2018b). Water structure: methods in Water Structure and Science.
Chou K-C, Jiang S-P (1974). Studies on the rate of diffusion-controlled reactions of enzymes. Spatial factor and force-field factor. Scientia Sinica 27(5): 664-680.
Collins JC (2000). Water: The Vital Force of Life. A Primer on Water in the Living Cell. Molecular Presentations, Kinderhook, New York 12106, p13.
Cooperative and Coherent Water (2010) in Water’s Quantum Jazz. Science in Society Archive, 27/09/2010.
Cotton FA, Wilkinson G, Gaus PL (1995). Basic Inorganic Chemistry, 3rd edition. Wiley (New York).
Cyranski JF (1985). Information theory and the problem of molecular structure. Found Phys 15(8): 833-849.
Dalton J, Milgrom LR (1980). Non-rigid molecules. Part 4. Hydrogen atom scrambling in the mass spectra of hydrocarbons. J Chem Soc Faraday Trans 2 76: 88-95.
Dawkins R (1988). The Blind Watchmaker. Penguin Books, London United Kingdom.
Deichmann U, Schuster S, Mazat J.-P, Cornish-Bowden A (2013). Commemorating the 1913 Michaelis-Menten paper, ‘Die Kinetic der Invertinwirkung’: three perspectives. In: FEBS Journal 2013.
Del Giudice E, Voeikov V, Tedeschi T, and Vitelli G (2015). Ch 5. The origin and the special role of coherent water in living systems in Fields of the Cell, (Eds. Fels D, Cifra M, and Scholkmann F), pp 95-111. Research Signpost 37/661 (2), Fort P.O. Trivandrum-695 023 Kerala, India, ISBN: 978-81-308-0544-3.
Diaz A, Loewen PC, Fita I, Carpena X (2012). Thirty years of heme catalases structural biology. Arch Biochem Biophys 525: 102-110.
Dominguez L, Sosa-Peinado A, Hansberg W (2010). Catalase evolved to concentrate H2O2 at its active site. Arch Biochem Biophys 500: 82-91.
Fersht A (1999). Structure and Mechanism in Protein Science. Freeman and Co, New York, p179.
Finney JL (1982). Solvent effects in biomolecular processes. In : Biophysics of water. Franks F, Mathias S (eds). J Wiley and Sons, New York, pp55-58.
Foroughi LM, Kang YN, Matzger AJ (2011). 60 years from discovery to solution: crystal structure of catalase form III. Acta Crystallogr D: Biol Crystallogr 67: 756-762.
Fridovich I (1998). Oxygen Toxicity: a Radical Explanation. J Exp Biol 201: 1203-1209.
Gallo P, Aman-Winkel K, Angel CA et al (2016). Water: a tale of two liquids. Chem Rev 116: 7463-7500.
Gamalay IA, Klybin IV (1999). Roles of ROS: Signalling and Regulation of Cellular Functions. Int Rev Cytology 188: 203-255.
Garcia-Viloca M, Gao J, Karplus M, Truhar DG (2004). Quantum mechanical methods for biomolecular simulations. Science 303(5655): 186-195.
Geiger A, Stillinger FH, Rahman A (1979). Aspects of the percolation process for hydrogen-bond networks in water. J Chem Phys 70(9): 4185-4193.
Giguère PA, Chen H (1984). Hydrogen bonding in hydrogen peroxide and water: a Raman study of the liquid state. J Raman Spectroscopy 15(3): 199-204.
Goldstein S, Meyerstein D, and Czapski G (1993). The Fenton reagents. Free Rad Biol and Med 15(4): 435–445.
de Grey ADNJ (2002). HO2: the forgotten radical. DNA Cell Biol 21(4):251-257.
Grima R, Schnell S (2006). A systematic investigation of the rate laws valid in intracellular environments. Biophys Chem 124:1-10.
Haller G and Beron-Vera F J 2013 Coherent Lagrangian vortices: the black holes of turbulence J. Fluid Mech. 731 R4-1–10.
Henri V (1902). Théorie générale de l’action de quelques diatases. C. R. Hebd. Séances Acad Sci 135:916-919.
Ho M-W (2012). Cooperative Coherent Water in Living Rainbow Water, pp 15-27. World Scientific. ISBN: 978-981-4390-89-7.
Imyanitov NS (2016). Dialectics and synergetics in chemistry. Periodic Table and oscillating reactions. Found Chem 18(1): 21.
Jones LL, Atkins P (2000). Chemistry: Molecules, Matter, and Change. WH Freeman and Co, New York, Ch 5, p382.
W. L. Jorgensen and J. D. Madura (1985). “Temperature and size dependence for Monte Carlo simulations of TIP4P water.” Mol Phys 56 (6): 1381.
Kalko SG, Gelpi JL, Fita I, Orozco M (2001). Theoretical study of the mechanism of substrate recognition by catalase. J Am Chem Soc 123: 9665-9672.
Karrasch D, Huhn F and Haller G (2015) Automated detection of coherent Lagrangian vortices in two-dimensional unsteady flows Proc. R. Soc. A 471 2173.
Kauzmann W (1959). Some factors in the interpretation of protein denaturation. Adv Protein Chem 14: 1-63.
Kent M (2000). Advanced Biology. Oxford University Press, Oxford, UK, p43.
Khan AU, Wilson T (1995). Reactive Oxygen Species as Second Messengers. Chem Biol 2: 437-445.
Klein RA (2006). Cooperativity in large water clusters liquid water, ice, and clathrates. NIC Symposium 2006 (G Minster, D Wolf and M Kremer eds), pp65-74, John von Neumann Institute of Computing, Julich.
Knowles JR, Albery JW (1977). Perfection in enzyme catalysis: the energetics of triosephosphate isomerase. Acc Chem Res 10(4): 105-111.
Koshland DE (1958). Application of a theory of enzyme specificity to protein synthesis. Proc Natl Acad Sci USA 44(2): 98-104.
Kohler RE (1973). The Enzyme Theory and the Origin of Biochemistry. Isis 64(2): 181-196.
Kurian P, Dunston G, Lindesay J (2014). Does quantum entanglement in DNA synchronise the catalytic centres of type II restriction endonucleases? arXiv:1403.5342v1 [physics.bio-ph] 21 Mar 2014.
Levi F, Mintert F (2014). A quantitative theory of coherent delocalisation. New J Phys 16: 033007.
Milgrom L (2016). Why is catalase so fast? A preliminary network hypothesis for the rapid enzyme-catalysed decomposition of hydrogen peroxide. WATER 7:129-146.
Miyake T, Roalndi M (2016). Grotthuss mechanisms: from proton transport in proton wires to biophotonic devices. J Phys Condens Matter 28: 023001.
Moin ST, Hofer TS, Randolf BR, Rode BM (2012). An ab initio quantum mechanical field molecular dynamics simulation of hydrogen peroxide in water. Comput Theoret Chem 980: 15-22.
Murthy MR, Reid TJ, Sicignano A, Tanaka N, Rossmann MG (1981). Structure of beef liver catalase. J Mol Biol 152: 465-499.
Olsen MMH, Siegbahn PEM, Warshel AJ (2004). Simulations of the Large Kinetic Isotope Effect and the Temperature Dependence of the Hydrogen Atom Transfer in Lipoxygenase. J Am Chem Soc 126(9): 2820-2828.
Partay LB, Jedlovszky P, Brovchenko I, Oleinikova A (2007). Formation of mesoscopic water networks in aqueous systems Phys Chem Chem Phys 9: 1341-1346.
Pollack GH (2013). The Fourth State of Water: Beyond Solid, Liquid, and Vapour. Ebner & Sons Publishers, Seattle, Washington US.
Pusuluk O, Farrow T, Deliduman C, Burnett K, Vedral V (2017). Proton tunneling in hydrogen bonds and its possible implications in an induced-fit model of enzyme catalysis arXiv: 1703.00789v1 [Physics.chem-ph] 2 March 2017.
Ramasesha K, Roberts ST, Nicodemus RA, Mandal A, Tokmakoff A (2011). Ultrafast 2D IR anisotropy of water reveals reorientation during hydrogen-bond switching J Chem Phys 135: 054509.
Reid TJ, Murthy MR, Sicignano A, Tanaka N, Musick WD, Rossmann MG (1981). Structure and haem environment of beef liver catalase at 2.5 Å resolution. Proc Natl Acad Sci USA 78: 4767-4771.
Riedel C, Gabizon R, Wilson CAM et al (2015). The heat released during catalytic turnover enhances the diffusion of an enzyme. Nature 517(533):227-230.
Rothen A (1979). Tryptic action across a membrane. Physiol Chem Phys 11(6): 481-9.
Rothen A (1982). Biological interactions taking place at a liquid-solid interface. Intern Rev Cytol 80: 267-303.
Rousseau DL, Porto SPS (1970). Polywater: polymer or artefact? Science 167: 1715-1719.
Saran M, Michel C, Bors W. (1998). Radical Functions in vivo: A Critical Review of Current Concepts and Hypotheses. Z Naturforsch [C] 53: 210-227.
Sorge A (2015). Pypercolate.readthedocs.io/en/stable/percolation-theory.html.
Solis-Calero C, Ortego-Castro J, Munoz F. (2011). DFT study of an amino-phospholipid surface-mediated decomposition of H2O2. J Phys Chem 115(46):22945-22953.
Stauffer D (1985). Introduction to Percolation Theory. Taylor and Francis, London and Philadelphia.
Streltsov A, Singh U, Dhar HS, Bera MN, Adesso G (2015). Measuring quantum coherence and entanglement. Phys Rev Letts 115: 0204043.
Stryer L, Berg JM, Tymoczko JL (2002). Biochemistry (5th ed.), WH Freeman, San Francisco, ISBN 0-7167-4955-6.
Sukumar N (2009). The chemist’s concept of molecular structure Found Chem 7: 11-20.
Tanford C (1968). Protein denaturation. Adv Protein Chem 23: 121-282.
Vainshtein BK, Melik-Adamyan WR, Barynin VV, Vagin AA, Grebenko AI (1981). Three-dimensional structure of the enzyme catalase. Nature 293: 411-412.
Voeikov V (2001). Reactive Oxygen Species, Water, Photons, and Life. Rivista di Biologia/Biology Forum 94: 193-214.
Watson J (1995). “The quantum of water and protein and the structure of the cell” chapter 5 in Quantum Worlds, WH Freeman and Co, New York, see www.dpedtech.com/QWrlds.pdf
Watterson JG (1991). The interactions of water and proteins in cellular function. Prog Mol Subcell Biol 12: 113-134.
Watterson JG (1997). The pressure pixel: unit of life? Biosystems 41: 141-152.
Wheeler JA, Ford K (2000). Geons, Black Holes,and Quantum Foam: a Life in Physics. WW Norton and Co Ltd, New York, p235.
Wooley RG (1978). Must a molecule have a shape? J Am Chem Soc 100(4): 1073-8.
Zheng J-M, Chin W-C, Khijniak E, Khijniak E Jr, Pollack GH (2006). Surfaces and interfacial water: Evidence that hydrophilic surfaces have long range impact Adv Colloid Interface Sci 127: 19-27.
Zeilinger A. Quantum Teleportation and the Nature of Reality. 2004. Online document at: www.btgjapan.org/ catalysts/anton.html Accessed March 21, 2008.
Web References
1. Enzyme Kinetics. www.uscibooks/changten.pdf. [04.18.2015].
2. Chaplin MF. Water structure and science. www1.lsbu.ac.ac.uk/water/memory_of_water.html
[03.13.2015]
3. Chaplin MF. Water structure and science. www.lsbu.ac.uk//water/watterson.pdf. [20th March 2015].
4. Chaplin MF. Water structure and science. “Grotthuss mechanism.” http://www1.lsbu.ac.uk/water/grotthuss.html#alt [02.01.2018]
5. See Baker C. Decomposing hydrogen peroxide
www.rsc.org/Education/EiC/issues/2007May/ExhibitionChemistry.asp
