 High Electric Susceptibility is the Signature of Structured Water in Water-Containing Objects
High Electric Susceptibility is the Signature of Structured Water in Water-Containing Objects
Tychinsky, V1*
1 Coherent Phase Microscopy Lab, Moscow Institute for Radioengineering, Electronics and Automation (TU), 78 Ver- nadsky Av, 119454 Moscow, Russia
* Correspondence: Ph: +7 (495) 4346792; E-mail: vtych@yandex.ru
Key Words: live cells refractivity, gels, interference microscopy, exclusion zones in water, water in cells
Received June 27th, 2011; Revised August 21st, 2011; Accepted November 15th, 2011; Published December 5th 2011; available online December 15th 2011
Summary
There are many indications that water is structured in thin layers adjacent to the surface. However, its physical parameters are difficult to access by direct measurements. The high sensitivity of optical interference methods enabled to detect the signs of the structured component in the water-containing objects of very different nature: near the nafion surface, the polyacrylamide gel, and the single mitochondrion and in the amoeba. The analysis of the published data on refractive indices led to the conclusion that a high value of the electric susceptibility (χ) is the common physical parameter of the structured water layers in the vicinity of hydrophilic surfaces. Its values χ ≅ 1.0-1.12 correspond to the equivalent refractive indices n = 1.41-1.45, significantly exceeding no = 1.333 for bulk water. Apparently, we are first to report that high refractive indices of water-containing objects are connected with the structured water component.
Article Outline
Introduction
There are many known facts from which one can deduce the altered properties and structure of water near the surface of solids, in the vicinity of hydrophilic surfaces, in gels, and in biological membranes [1-3]. The thickness of exclusion zones (EZ) with significant changes in physical parameters – the potential gradient, pH, concentration of impurities, the diffusion coefficient reached tens or hundreds of microns [4, 5].
Changes in the optical properties of water in the exclusion areas, to our knowledge, have not received a satisfactory explanation. One of the paradoxes that to our knowledge has not been discussed in the literature is as follows. Some gels and biological objects with large (up to 95-99%) proportion of water have a refractive index (RI) (n = 1,42-1,50), significantly higher than RI (no = 1,333) of ordinary water. A natural question arises: is the high value of RI an attribute of structured water? We here show that analysis of published data allow us to give a positive answer to this question.
First we note the results of only two experimental works that at first sight have nothing to do with the problem of water in biological objects. The refractive index of water in the immediate vicinity of nafion was high (n ≅ 1,455) and decreased monotonically down to the standard values of no at the distance of 40-50 μm [6]. This result can be seen as a consequence of reducing the proportion of structured water away from the hydrophilic nafion surface. Other non trivial phenomenon consisted in change in the polyacrylamide gel RI in the vicinity of the temperature phase transition [7]. The RI of the gel decreased sharply up to the standard value of no ≈ 1,333 with the increase of the gel temperature from 33º to 36º C.
Finally, high RI values, depending on the medium composition, have been observed in various biological objects in [8-12]. In isolated mitochondria the RI varied within the range n ≅ 1,335-1,42 [9,10]. High RI values (n = 1,46-1,50) were measured in the testate amoeba with a holographic digital microscope [8]. We do not dwell on the details of experiments in [6-12] since in this case those details are not very important.
Methods
We use the electric susceptibility as a basic parameter of a medium in the following analysis of optical properties of water-containing objects. This does not contradict the commonly used refractive indices, as they are linked with the known formulae
(1) ε = 1+χΣ = nΣ2
Here ε is the dielectric constant, nΣ – the refractive index of the multi component medium, χΣ – its electric susceptibility (ES). Contrary to RI, ES satisfies the condition of additivity, and is used here to represent the susceptibility of the multi component object as the sum of components
(2) χΣ = Σχi = Σήi<χi>
In equation (2), χi = ni2 – 1 is ES of the i-th component, ήi is its weight fraction that meets the condition of normalization Σήi = 1. Note, that <χo> = no2 – 1 = 0,777 is a well known constant for pure “bulk” water without additives (ήo = 1). We consider the condition of coexistence (or additivity) (2) as the essential prerequisite in this work for separation of the structured water component’s contribution. This allows in the frame of a unified model to evaluate the susceptibility of the structured water components in various water-containing objects.
To designate components, we use here the following indices: 0 – for the abstract «bulk» water; 1 – for the bulk water in the real medium; 2 – for admixtures (for example, “dry” substance or polymer); 3 – for the component of structured water.
Results
The above mentioned values of RI of water in the vicinity of the nafion surface [6] can serve as a signature of the structured water features. In [6] it was shown that the refractive index nΣ(х) near the nafion surface reaches a maximum (nΣ ≅ 1.455) and decreases to the standard value. The fall of the RI with increased distance could be well explained in the framework of the two-component model system by the changes of the fraction of structured (ή3) and bulk water (ή1 = 1 – ή3).
Under assumption that all water molecules are structured (ή2 = ή1 = 0; ή3 = 1) in the vicinity of the nafion surface the maximum value nΣ ≅ 1.455 can be used to evaluate with the formula (1) the ES of the structured water component (χΣ)max = χ3 = <χ3> ≅ 1.117. The data of [6] allow us to calculate by the formula ή3(х) = [χΣ(x) – <χ1>]/(<χ3> – <χ1>) the change in fraction of the structured water component with increasing distance from the nafion surface. The graph in Figure 1 shows that at the distance of x ≈ 12 µm the water fractions are equal.
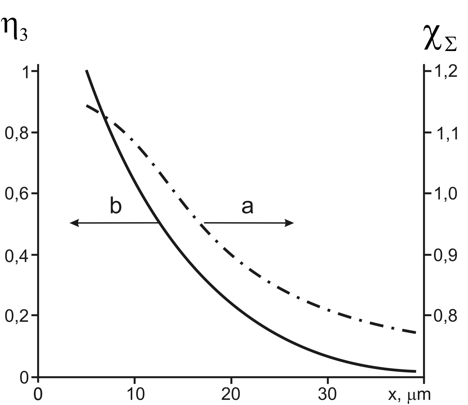
Figure 1: Changes of water optical properties near the nafion surface [6].
a) The dependence of the calculated water susceptibility on the distance from the nafion surface.
b) Decrease of the structured water share. The portions of bulk and structured waters were equal at the distance x ≈ 12 µm from the nafion surface.
The second convincing example of an enhanced refractive index that can be attributed to a component of structured water is given in the paper [7], which is concerned with measurements of polyacrylamide gel (PNIPAM). When heated from T = 33ºС to Т = 36ºС its RI at λ = 500 nm in the course of the temperature phase transition decreased from nmax = 1.45 tо nmin = 1.345. Estimating the fraction of structured water should take into account the following considerations. It is known that the proportion of water in gels is very high (90-95%). This is the basis for the assumption that the contribution of polyacrylamide to refractivity is not large (χ2 << χ1) and that its changes (if any) in the course of temperature transition (Т = 33 – 36º С) do not significantly affect nΣ. The gel component’s numerical contribution can be evaluated using formula χ2 = ή2<χ2> = (nmin)2 – 1 – χ1 ≅ 0,032. To estimate susceptibility (<χ3>) of the gel’s structured water component we presented the gel RI (nΣ) in two indicated states through formulas:
(3) (nmin)2 = 1+χ1 + χ2 ; for Т > Тcr (ή1 + ή2 = 1) and (nmax)2 = 1+χ3 + χ2; for Т < Тcr (ή3 + ή2 = 1)
From (3) follows for the structured water susceptibility <χ3> = [χ1 + (nmax)2 – (nmin)2]/ή3.
Calculations showed (see Figure 2) that the susceptibility varied within <χ3> = 0.98-1.07 and because of optical dispersion depended significantly on the wavelength. These values correspond to the structured water RI n3 = 1,41-1,44.
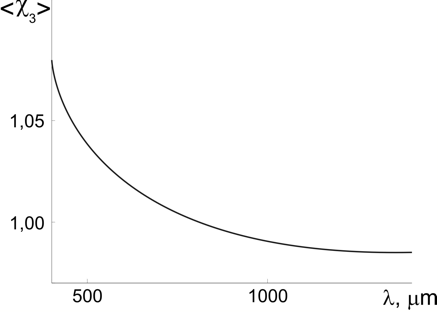
Figure 2: The calculated dependence of the susceptibility of the gel’s structured water component on wavelength [7].
We will use the above representation of medium as the sum of components when analyzing the susceptibility of the structured water in a single mitochondrion [14, 15] and testate amoeba [8]. The mitochondrion we consider here as the two-component medium consisting of “dry” substance and water. We assume that, similarly to the above example, water can only be in two states: bulk and structured.
The measurements of the volume-averaged RI (<nΣ>) of a mitochondrion showed [9,10] that the addition of rotenone decreased it to the minimum value <n>min ≅ 1.34, while the ATP stimulation raised it to <n>max ≅ 1.44. We assume that in the case of mitochondria, optical properties of “dry” substance are determined predominantly by the membrane phospholipids and built-in proteins, and these contributions do not considerably change in the course of mitochondrion activation. The small difference between <n>min ≅ 1.34 and no = 1,333 is considered as indication of a minor contribution the “dry” substance. This corresponds the estimated ES (χ2 ≅ 0,02-0,025) and weight (ή2 ≅ 0,02-0,025) values and to the quite realistic phospholipids’ RI (<n2> ≅ 1.4-1.5) and ES (<χ2> ≅ 1,0-1.1).
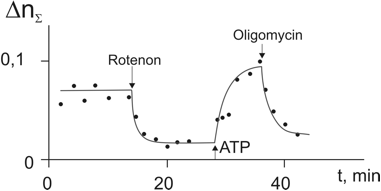
Figure 3: Change of refractive index of a single mitochondrion under the action of inhibitors (rotenone and oligomycine) and ATP stimulation [9-12]. Extreme values were used to estimate the structured water susceptibility.
To estimate <χ3> value in the activated mitochondrion we suggested [9,10] that all water molecules are structured (ή1 = 0; ή3 = 0,98) while in the deactivated mitochondrion water remains bulk (ή1 = 0,98; ή3 = 0). We also assume that “bulk” water parameters are close to those of “pure” water (<no> = 1.333; <χ1> ≅ <χo> = 0.777). Under these assumptions from the formulas (4) follow the values χ2 ≅ 0,02-0,025 and <χ3> ≅ 1.07. As noted above, that the high refractive indices were observed in many water-containing objects, and this phenomenon is quite universal in nature. To explain these effects the so called “hydrate” hypothesis [10-12] was suggested according to which the structured water molecules in the layers adjacent to the charged membrane acquired higher electric susceptibility.
Our conclusion about the high susceptibility of structured water in biological objects is in accord with analysis of the testate amoeba measurements [8]. In the “map” of refractive indices of the testate amoebathe minimum values were n ≅ 1.46. It is natural to assume that this value of the RI is associated with the component of the structured water. An estimate yields the value of susceptibility<χ3> ≅ 1.10-1.12 larger than <χ2> ≅ 1,0-1.1 in mitochondria.
Conclusion
The above estimates of susceptibility of the structured water component leads to several important conclusions. The closeness of the electric susceptibility values among different specimens (<χ3> ≅ 1.05-1.12) is somewhat unexpected, since the nature of the objects is very different. These values correspond to the equivalent refractive index values of the structured water within <n3> ≅ 1.42-1.45 significantly exceeding no = 1.333 of the pure bulk water.
We believe that the proposed by G. Pollack concept EZ [4, 5, 13] is consistent with the analysis presented here, and confirms the possibility of its application to biological objects. It should be noted that signs of structured water in the form of «metabolic» component of refractivity were observed in various biological objects, including cyan bacteria Anabaena and Synechocystis, spores, and chloroplasts [10, 11].
We note also that ordering water molecules between phospholipid bilayers has been visualized by coherent anti-Stokes microscopy [3]. The main result of this analysis is the assertion that the high susceptibility is a sign of the structured component of water in objects of different nature. We assume that the approach proposed here can be used for the analysis of structured water in the broader class of objects – on solid-state surfaces with different physical and chemical properties, in the hydration shells of macromolecules, and in polymers, gels and alcohol solutions.
Acknowledgements
The author is grateful Dr. V. Nadtochenko and Dr. A. Shtil for discussion and to assistant professor A. Kretushev, PhD, for his help and discussion of the results.
References
[1] Chaplin M. F. (2011). Water structure and science. Ion hydration and aqueous solutions of salts, http://www.lsbu.ac.uk/water/ions.
[2] Chaplin M. F. (2000). Biophys. Chemist., 83: 211-221
[3] Cheng Ji-Xin, Pautot S., Weitz D., Xie X.S., (2003). Ordering of water molecules between phospholipid bilayers visualized by coherent anti-Stokes Raman scattering microscopy, PNAS, 100(17): 9826-9830
[4] Pollack G., (2001). Cells, Gels and the Engines of Life, Ebner & Sons.
[5] Cameron I., Fullerton G., (2006). Ch. 16. Non-bulk-like water in cellular interfaces. In: Water and the Cell, Ed. Pollack G., Cameron I., Weatley D., Springer
[6] Bunkin N.F. (2010). Study of refractive index of nafion spheres in water and other solvents; effect of exclusion zone, Abstracts WaterConference
[7] Garner B., Cai T., Ghosh S., Hu Z., Neogi A., (2009). Refractive index change due to volume-phase transition in polyacrylamide gel. Appl. Phys. Express 2;057001
[8] Charriere F., Pavillon N., Depeursinge C., Heger T., Mitchell E., Marquet P., Rappaz B., (2006). Living specimen tomography by digital holographic microscopy: morphometry of testate amoeba, Optics Express 14(16): 7005-713
[9] Tychinsky V., Kretushev A., Vyshenskaja T., (2004). Mitochondria optical parameters are dependent on their energy state: a new electrooptical effect? Eur. Biophys. J. 33(8): 700-705
[10] Tychinsky V., (2009). The metabolic component of cellular refractivity and its importance for optical cytometry, J. of Biophotonics, 2(8-9), 494-504
[11] Tychinsky V.P., Tikhonov A.N., (2010). Visualization of individual cells and energy-transducing organelles, Cell Biochem and Biophys., 58(3): 117-128
[12] Tychinsky V.P., (2007). Dynamic phase microscopy: is a “dialog” with the cell possible? Phyics-Uspekhi 50(5): 513-528
[13] Zheng J.M., Pollack G.H., (2003). Long-range forces extending from polymer-gel surfaces, Phys. Rev E, 68(3 Pt 1): 0311408
Discussion with Reviewers
Anonymous Reviewer: If there is a gradient of susceptibility near the protein or polymer surface, do you have any estimate of the value immediately adjacent to the surface?
Vladimir Tychinsky: Dipole moment of the water molecule is limited and so enhanced gradient of susceptibility near the protein or polymer surface in the hydrate shell is low-probable. I suppose that maximum value of susceptibility is near the unit.
Reviewer: Can you say a few words about the prospect of using susceptibility measurements as a diagnostic tool for detection of pathologies?
Tychinsky: Good question. Really, susceptibility displays the functional state change of the live cell and its organelles. The problem consists in finding the algorithms, which allow defining these parameters in the images of a live cell. Solution of the problem will be a base of new methods of in vitro diagnostics of a cell and its donor.
