Allometric Scaling Behaviour – A Quantum Dissipative State Implies a Reduction in Thermal Infrared Emission and Fractal Ordering in Distilled Coherent Water

Johansson B^1*, Sukhotskaya S¹

¹ Akloma Bioscience AB, Medeon Science Park, 212 05 Malmö, Sweden
* Correspondence: E-mail: benny@akloma.com

Key Words: Water ordering; Reduction in IR emission; Fractal scaling; Long-range correlation; Self-regulation

Received July 24, 2011; Accepted October 17, 2011; Published January 22, 2012; Available online February 22,2012

doi: 10.14294/WATER.2011.9

Summary

According to classical theory, the impact of various hydrophilic surfaces on the contiguous aqueous phase extends from a few water-molecular layers to several hundreds of microns. Our studies support evidence that irradiation by low entropy sunlight expands the ordered water state comprising the entire bulk volume of liquid water, irrespective of a polar or non-polar surface state. Thermal IR imaging as well as measurement of allometric scaling behavior and redox-potential identified physically distinct concentric and condensed temperature gradient zones with long-term consistency, aligned as a structural coherence that implies a considerably decreased mobile water state. A strong power law relationship in the fractal scaling boundary revealed that fractal scaling geometry is part of water ordering and that thermal IR flickering relates on a long-range correlation between water molecules.

Introduction

Coherent Water

The existence of density fluctuations between a coherent tetrahedral-like, hydrogen-bond distorted structure in water was recently demonstrated at ambient conditions (Wernet et al., (2004; Huang et al., 2009). A temperature-dependent fluctuating equilibrium model of the two types of local structure was proposed; a low-density liquid (LDL) with a low entropy highly ordered coherent state at ambient temperature and a high-density liquid (HDL) with a high entropy state and a less ordered structure at temperatures close to the boiling point. The highly ordered domains of an approximate length of 1-2 nm consist of 50-100 water molecules (Huang et al., 2009). The length-scale of the tetrahedral coordinated structure is fairly constant, but its number decreases at higher temperatures. In liquid water, the distribution of the spatial geometry of the hydrogen bond, i.e. hydrogen-bond length and angle, revealed a substantial temperature-dependent distortion of the hydrogen-bond network, which is responsible for the neighboring long-range spatial correlations at higher temperatures (Modig et al., 2003).

The polymorphism of liquid water as recently suggested by Mallamace (Mallamace, 2009) represents a new understanding of water, the most complex liquid with 67 known anomalies and most abundant substance on earth (Web ref. 1). Most important is that some water-anomalies can now be explained by the two coexisting water-liquid states with different structural configurations; i) the coherent LDL-like local structure persists not only at super-cooled (Banerjee et al., 2009), but also at ambient conditions, ii) the presence of two local maxima in the structure-related specific heat (Mallamace, 2009; Mallamace et al., 2008), i.e. a difference in storage capacity of structural configurative energy, reflecting the change in distribution between the two liquid water phases.

Long range surface-induced ordering of water has been known for decades as recently cited (Zheng and Pollack, 2003), where the thickness of the ordered layer can reach hundreds of microns, thus altering hydrophilic interfacial and air-liquid water surfaces (Zheng and Pollack, 2003; Ling, 2003; Zheng et al., 2006; Pollack, 2008). The significant importance of this water is the long range layer by layer growing and ordering of water molecules, despite the disruptive effects of thermal motion. The exceptional long-range stability that holds the molecules together exceeds the capacity of the ordinary hydrogen bond, which is limited to only a few water molecular-layers (Del Giudice, 1985; Zheng and Pollack, 2003).

Long distance attraction of molecules and feedback dynamics reflecting the self-organization ability of the water system involve an extended coherence of the inherent oscillations produced by the system (Froehlich, 1969; Del Giudice, 1985). The coherent LDL domains of water appear to be a source of extended electromagnetic fields able to couple with local and distant water molecules and alter oscillations related to the level of excitation supplied by the photons generated and self-trapped within coherent domains (Del Giudice et al., 1986; Del Giudice et al., 1988; Del Giudice and Vitiello, 2006; Del Giudice and Tedeschi, 2009). The energy of the water system contracts and condenses – increasing its density. The coherent oscillations couple with thermal fluctuations, cooling the water and generating a flicker-regulated distribution towards a more coherent LDL state (Del Giudice and Tedeschi, 2009).

The physical and chemical conditions in long-range interfacial water are very different from those in ordinary or bulk water, thus it can be considered the forth-aggregate state of water (Zheng et al., 2006). Special properties include higher viscosity and density, lower freezing temperature and relative permittivity, UV absorption peaks of around 270 nm and fluorescence emission in salt solutions in the range of 480-490 nm (Zheng and Pollack, 2003; Ling, 2003; Zheng et al., 2006; Pollack, 2008; Derjaguin, 1987). Interfacial water has a negative electrical potential different from bulk water down to -150 mV (Ling, 2003). The thickness of the layer increases when illuminated by visible and, in particular, IR radiation, giving a peak at 3100 nm.

The negative electric potential and the response to the energy of incident light strongly suggest that electrons in this water are at a much higher state of excitation than those in bulk water and that fairly low excitation energy is needed to free them (Voeikov and Del Giudice, 2009). Exposure to thermal IR radiation not only expands the thickness of the interfacial layer, but also the electron-donating or reductive capacity. In the coherent LDL domains, as opposed to the HDL state where all electrons are tightly bound locally, the quasi-free electrons can be excited and form frictionless vortices with an extremely long lifespan (Del Giudice and Tedeschi, 2009). The extended life span, lasting for days or weeks, depends on a self-regulated magnetic moment that aligns coherent intrinsic and external vortices that cannot degrade thermally (Del Giudice and Tedeschi, 2009; Elia and Napoli, 2004). The coherent domains act as reservoirs, storing a large amount of energy and transforming it from HDL high entropy to LDL low entropy energy. The highly ordered energy of coherent clusters makes the water molecules oscillate at the same frequency as the coherent domains, accumulating in a more symmetrical and stable structural long-range molecular network (Del Giudice and Tedeschi, 2009).

Highly ordered long-range correlation changes interfacial water into a crystalline-like state with local and distant configurative physical properties (Chai et al., 2008), e.g. the capacity to exclude colloidal solutes from the coherent zone (Chai et al., 2008; Wiggins, 2002) and promote growth of a crystalline tree-like branching structure expanding from the polar surface into the bulk volume of water (Ling, 2003). The change towards a locally arranged negative electric potential with a simultaneous increase in pH around the growing branches indicates self-regulative dynamics connected with long range oscillation and lowering of the intrinsic entropy, giving rise to structural ordering and allometric scaling behavior (Vitiello, 2009a; Vitiello, 2009b) all of which are characteristic of a dissipative structure (Turning, 1952; Prigogine and Nicolis, 1977; Del Giudice, 2009).

Allometric Scaling of Water

Allometric scaling relationships in nature and biology are considered to be the branching model that fulfills the principles of a fractal network, possessing repeating self-similar unpredictable patterns when viewed at increasingly fine magnifications (Mandelbrot, 1983). The model predicts structural and functional properties and analyses scaling relations of distribution networks in animate systems, e.g. structural diversity of all organisms, the main part of the power law for metabolic rate and how energy is distributed with minimal dissipation on different levels of structurally ordered pathways in nature (West et al., 1997). The fractal dimension is a quantitative estimate and non-integer value (between 1 and 2) that measures the degree of fractal boundary fragmentation or irregularity over multiple scales (Mandelbrot, 1983).

The allometric scaling model has been applied to both closed and open fractal water networks (Biondini, 2008), i.e. open water systems that exchange energy and entropy with the environment (Del Giudice, 2009). When LDL domains receive external energy and use it to change the allometric dimension of a given structure into a fractal or more desirable fractal architecture, a new structure with new output energy is produced, e.g. for water uptake by plant roots (Biondini, 2008), for variation in pH time series from the inlet and outlet of lake water (Huang, 2010), for ensuring that the growth of water trees in a dielectric medium follows an estimate of fractal dimension (Luo, 2003) or for localization of snowflake structural domains (Daudert and Lapidus, 2007).

Functional Water

Functional water denotes water to be used in biological contexts in accordance with the definition of functional food (Diplock et al., 1999). The functional quality of water restores self-regulative physiological conditions to maintain homeostasis (Asp, 2001; Johansson, 2009; Johansson 2008b). The physical and chemical conditions of functional water are distributed in the entire bulk volume, not only adjusting polar surfaces towards the long-range coherent state of liquid water (Johansson, 2008a; Johansson 2008b). The physical and chemical qualities of coherent water have been identified in bulk water when transformed by means of water splitting into a lasting excited high-energy state of ordered water (Ikeda, 1999) and exposed to very mild ground state energy conditions, such as the influence of a topological geometrical field grid/raster (present study)(Johansson, 2008a), vortex agitation, freezing-thawing, evaporation-condensation, audio-sonication, capillary filtration, oscillating electromagnetic fields (Domrachev et al., 1992) and water agitation with metal oxides (Ikeda, 1999).

Functional water may be a significant factor in the self-regulation of homeostasis. On the basis of the theory of dissipative systems’ ability to self-regulate (Prigogine and Nicolis, 1977), it was hypothesized that the transformation of ordinary water into functional water may imply that organized incident light (Johansson, 2008a) is imperative for entangling and increasing the number of water molecules and for storing stabilizing energy in the coherent domains. The present study was designed to investigate the thermal fluctuation and cooling effect of expanding coherent domains in functional water by means of thermal IR emission. Additionally, the hypothesis implies that the thermal flickering in IR emission is correlated with a change in the fractal dimension of thermal images and that the reservoir of quasi-free electrons generates a reduction in the redox-potential with a concomitant change in pH.

Materials and Methods

Water Conditioning

Distilled water (50 ml)(Apoteket AB, Sweden) stored in a transparent plastic bottle (Nalgene dilution bottles, Fisher Scientific, Gothenburg, Sweden), with a topographic geometrical matrix (TGM)(Johansson, 2008a) connected via the wall of the bottle was exposed to incident daylight and conditioned for 24 h at ambient (23 °C) temperature. For the control experiment, distilled water was similarly exposed to daylight without TGM. The bottles were stored at ordinary ambient indoor conditions during the study.

The long-range coherent qualities of functional water were obtained by incident daylight passing a transparent topographic geometrical field grid/raster. The geometrical grid imprinted on a plastic substrate causes ordinary photons to self-organize spatially with fractal symmetry, lower entropy and higher intensity. The highly ordered incident photons are tentatively accumulated and self-trapped with extended coherent domains that prescribe a co-oscillation with water molecules in the liquid state, thus reorganizing into a field-like ordered unification of bulk water molecules.

Infrared Emission Imaging

The IR image frames are produced by a RAZ-IR Thermal camera system (8-14 µm LWIR, thermal sensitivity ≤100 mK at 30 °C, thermal resolution 160×120 pixels/frame, 25 µm; Sierra Pacific Innovations Corporation, US). The equipment was set up in a very clean and closed room used for analytical measurements. A sheet of aluminum foil was placed on a table beneath the camera for standardization of background emissivity. The camera was mounted and fixed on a plastic stand and assembled vertically with the lens focused 7 cm (fixed position) from the top of two standing optical quartz cells (45x10x10 mm; Tamro Med-Lab, Gothenburg, Sweden), containing 5.0 ml of control or conditioned distilled water. Alternatively, two optical polystyrene cells (45x10x10 mm; Sarstedt, Aktien Gesellschaft & Co. D-51588, Nümbrecht, Germany) were used to investigate formation long-range correlations in water independent of polar cell surfaces. The cells were positioned and fixed in an upright position 1.0 mm apart and conditioned at room temperature for 60 minutes before measurement. Following “power on.” the camera automatically performed three Non Uniformity Calibrations (NUC) 5, 25 and 45 seconds after switch on. While turned on, the camera automatically performs NUCs at regular intervals. NUC allows automatic clean up of the image noise, ensuring the normalization and sharpness of the live image. Three repeated image frames were made in sequence on the water samples and saved for imagery analysis (temperature profiles of the pixel area and graphical representation of temperature data) with IR Analyzer software. The temperature data were obtained from a defined pixel area, covering the water surface area in each of the two cells, transferred to numerical data by the IR Analyzer software and exported to an excel sheet for statistical evaluation.

Redoxpotential and pH

The oxidation-reduction potential (ORP) and pH in distilled water were measured using an Inolab 740 multifunctional meter (WTW International, Stockholm, Sweden). The ORP was measured with a SenTix®ORP electrode (WTW International, Stockholm, Sweden). Measurement of pH in non-buffered solutions was performed with a high stability pH electrode (Schott A77803K). Both electrodes were located 2 cm below (bulk volume of water) the surface of the water sample. The ORP and pH electrodes were calibrated on a daily basis. The platinum surface of the ORP electrode was restored and reduced at ordinary measurement conditions before each measurement of water in 1.0 M Nitric acid for 15 min (Gileadi, 1975). The variation in electrochemical stability of the ORP electrode was within ± 5 mV. The ORP in control or TGM conditioned distilled water (25 ml) stored in a 30 ml plastic or glass beaker (Fisher Scientific, Gothenburg, Sweden) was measured every 60 sec for 120 min. The pH was followed in 25 ml of water for 90 minutes to reach stability. Data were collected with a PC and Multilab® pilot software. The ORP and pH were measured as the mean ± SD of triplicate experiments on each of six water samples.

Fractal Dimension and Detrended Fluctuation Analysis

The fractal dimension, FD, was calculated on thermal graphic black & white images by transformation and masking IR colorized images using the Box-Counting method with Benoit 1.3 software (Web ref. 2). The method covers the image with a computerized mesh of identical size d squares in the 2D-plane. The number of squares N(d) with a self-similar pattern was counted. For comparison, decreasing square size repeatedly fills the image with the pattern at different magnifications, whereby scale invariance, a characteristic of a fractal pattern, can be identified. The fractal dimension FD is an estimate of the linear portion in log scale of the behavior of the power law function;

N(d) = 1/d^FD

A set of three measurements on the thermal IR graphics gave the mean FD value.

Detrended fluctuation analysis (DFA)(Peng, 1994; Web ref. 3) determines the fractal scaling behavior of a numeric, e.g. time or temperature series data in the presence of possible trends without knowledge of their origin. The DFA algorithm permits the detection of intrinsic self-similarity embedded in a non-stationary time series. The root mean square fluctuation of the integrated and detrended time series F(n) behaves as a power law function of n;

(F(n) α n^d)

The integrated time series is divided into boxes of equal length n. For each box of length n, a least square line is fitted to the data. The calculation is repeated over all time scales (box sizes). The DFA exponent (d) is defined as the slope of the regression line log n vs. log F(n). A DFA exponent ranging from 0.5 ≤ d ≤ 1 indicates long-range power-law correlations, growing stronger towards 1. The change in the DFA exponent was calculated on mean temperature data from thermal IR emission pixels obtained on water.

Statistics

Descriptive statistics were evaluated by means of the SPSS statistical system. Data are presented as mean ± standard deviation and a probability level of p < 0.05 was considered significant.

Results

Reduction in Thermal IR Emission and Temperature

The water layer of the control sample next to the interfacial highly polar surface of the quartz cell is characterized by the ordering of water molecules (100-1000 µm thick layer) and a lower temperature that differs from bulk water (Figure 1a). From the thermal IR control image, the structural ordering and thickness of control water demonstrate that the red colour zone (temperature decreases according to the scaling; blue-blue/red-red and dark red) along and close to the quartz surface is in the range of up to 1000 µm. The IR emission of the more distant regions in the centre radiates normally. The IR emission from conditioned water (Figure 1b) immediately adjacent to the interfacial zone expands and entirely covers the water surface. The structural ordering and thickness of the high symmetry layer is in the range of up to 5000 µm.

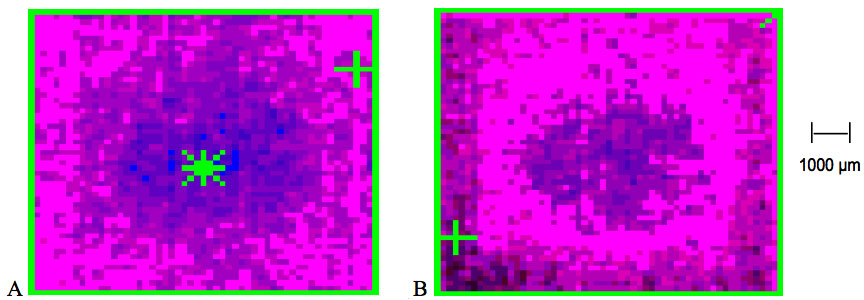
Figure 1: Thermal IR emission at room temperature in control (A) and conditioned distilled water (B) stored in quartz cells. The image frame of conditioned water depicts a higher state of structural organization and thickness of the symmetry layer up to 5000 µm from each of the cell walls. The mean temperature difference was 0.30 °C lower in experimental water. The temperature is decreasing according to the scaling; blue-blue/red-red and dark red color.

Several days’ repetitive analysis of image frames obtained on conditioned water tuned the reduction in thermal IR emission into a significantly decreased water surface temperature (Table 1). In addition, the hydrophilic surface of the quartz cell and the hydrophobic moiety of the polystyrene cell represent a region with an unexpectedly extensive long-range ordering capacity (Figure 2). The ordered molecular structure in conditioned distilled water obtained in the hydrophilic environment of the quartz cell generated a decrease in mean surface temperature of 0.30 ± 0.05 °C (P<0.001). The mean temperature difference in the hydrophobic polystyrene cell was 0.31 ± 0.04 °C (P<0.001) lower in the ordered water.

Table 1: Thermal infrared (IR) emission imaging, fractal scaling, redox potential and pH in control and conditioned distilled water.

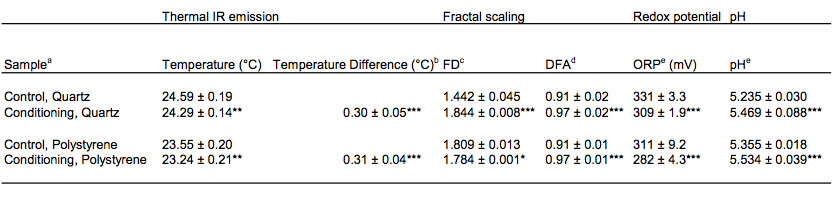
*P<0.05; **P<0.01; ***P<0.001
^a Water stored in quartz or polystyrene cells. All values are an average of six water samples, each calculated on three repetitive image frames taken in sequence. Samples were analyzed occasionaly during three days.
^b Temperature difference was calculated on numerical pixel data.
^c FD = Fractal dimension calculated on black and white images of thermal emission obtained from pixel areas.
^d DFA = Detrended fluctuation analysis calculated on serial sets of numerical temperature values according to pixel data.
^e ORP and pH were analyzed separately and independent of thermal IR measurements.

Figure 2: Thermal IR emission at room temperature in control (A) and conditioned distilled water (B) stored in polystyrene cells. The image frame of conditioned water illustrates a long-range correlation independent of a polar cell surface. The higher state of structural organization extends from the cell wall and forms a concentric IR emission gradient towards the cell centre (highest IR emission). The mean temperature difference was 0.31 °C lower in experimental water.

Importantly, the test in the polystyrene cell revealed a significantly lowered IR emission (Figure 2b) independent of hydrophilic surface. Likewise with the hydrophilic environment the high state of structural organization in the hydrophobic cell forms a concentric IR emission gradient, which declines in magnitude towards the cell centre. The thickness of the high symmetry layer follows the emission gradations and covers the entire cell surface. The IR radiation is less intensive in darker zones at hydrophobic compared to hydrophilic conditions. Since the difference in the IR emission between the two samples equals a tuned decrease in surface temperature, the lower emission substantiates an intrinsic ordering of water molecules that occur irrespective of the nature of the interfacial contact.

Considering the accumulated thermal IR emission, a significant difference (p<0.001) between control and conditioned data lines was observed (Figure 3a). Thus, the organized incident light induces an ordered water state with lowered emissivity and surface temperature. The fractal behavior and a low entropy state of incident photons lead to a lower energy position, which aligns with the magnetic moment of the freely movable electrons of coherent water domains that supports the ordered and sustainable coordination of water molecules. The coordinated species do not become thermally excited because they are too strongly tetrahedral to support vibrations other than the exact quality of resonating energy. The accumulated distribution of thermal IR emission registered at each increment change of 0.1°C illustrates this discrepancy, with lowered mean thermal IR emission and distinctive concentric temperature gradients (Figure 3b). The main temperature peak shifted in intensity from 25.5 % (control) to 18.2 % (conditioning) and equally in temperature from 24.8 °C to 24.4 °C. The total area under the curve was flattened out with lowered temperature and increased variance in the gradients ranging from 23.6 – 25.2 °C (conditioning) compared to 24.2 – 25.3 °C (control). The lowered emission makes the condensed gradients increase their density towards the centre (Figure 4a compared to 4b). The coherent concentric fractions of the temperature gradient tighten up and become smaller towards the cell centre. Many small vortex-like motions cause the alignment of the concentric temperature gradients (Figure 4b). The horizon profiles (Figure 5) obtained from the thermal IR emission outlines presented in Figure 1 reveal the change and variation in surface temperature and the reduced leaking of thermal IR emission from coherent oscillations of surface water. The sharp difference in surface temperature along the abscissa between the two samples and the more irregular fractured shape of the temperature horizon in organized water demonstrates a scale fractal-like invariance common in many natural shapes. A lowered temperature zone of increased magnitude was registered in the proximal temperature zone within ~1000-1500 µm (columns 2-8) of the cell wall (Figure 5b). Thus, an extended and sustained mixed gradient connecting the interfacial and distant coherent water is present.

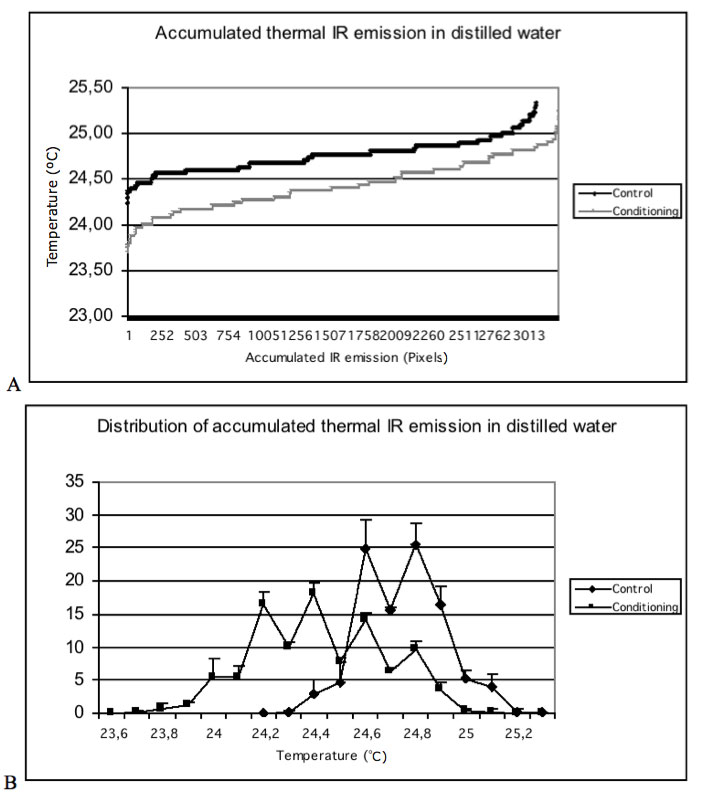
Figure 3: Accumulated thermal IR emission (A) and the mean ± SD percentage distribution of accumulated thermal IR emission (B) in control and conditioned distilled water stored in quartz cells (A). Three repetitive IR image frames were taken in sequence on the water samples for calculation of the thermal profiles. The temperature at each increment change of 0.1 °C was quantified transferring defined pixel areas into numerical temperature data.

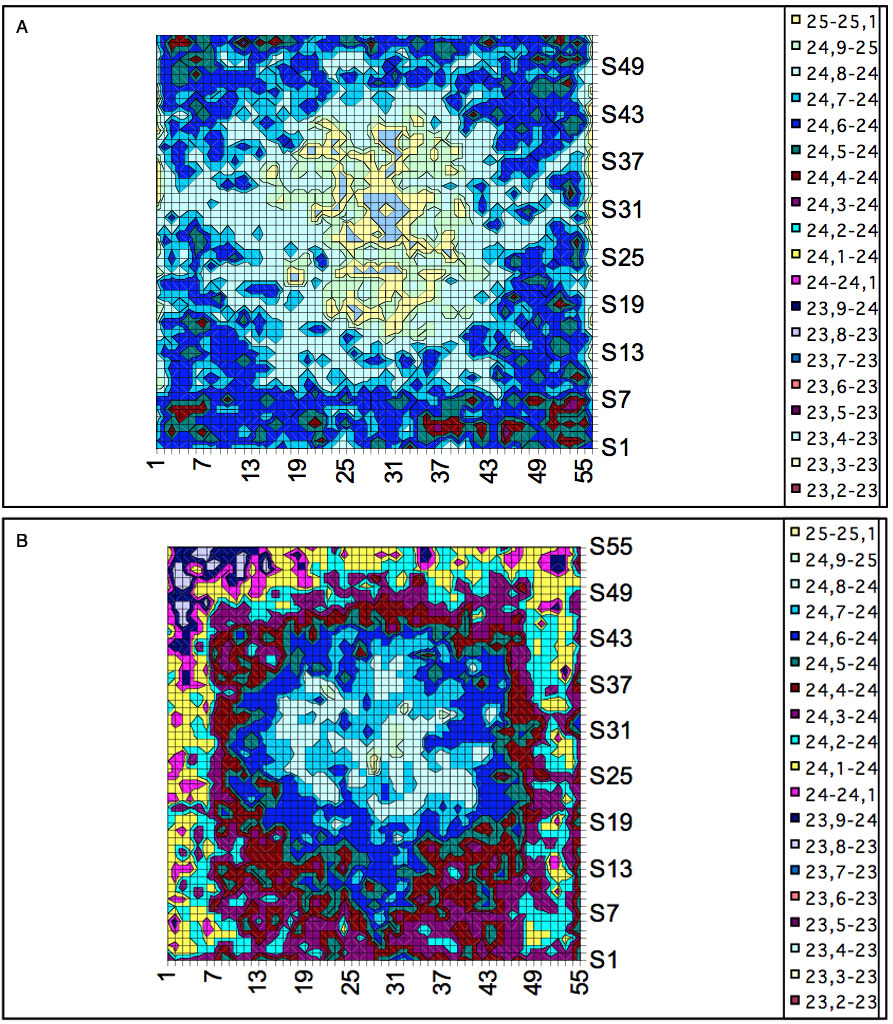
Figure 4: Thermal IR temperature profiles at room temperature in control (A) and conditioned distilled water (B) according to Figure 1. The temperature scaling was transferred from thermal IR numerical data. The temperature scaling was identical in both figures. Each grid equals a 25 x 25 µm pixel square area.

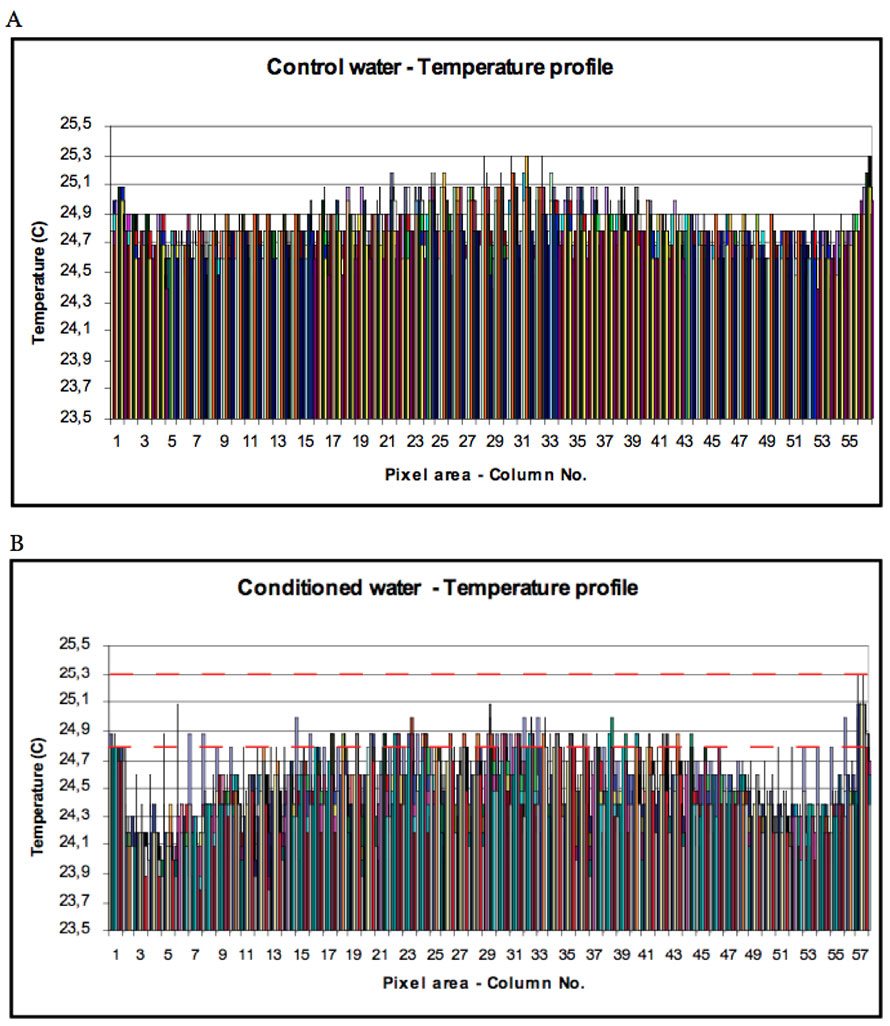
Figure 5: Thermal IR emission profiles at room temperature in control (A) and conditioned distilled water (B) according to Figure 1. The temperature horizon outlines show the change in distribution of the surface temperature and non-thermal motion from the left cell wall towards its centre and to the opposite cell wall. Each column segment on the abscissa represents the sum of 55 pixel squares on the ordinate. Columns are added segment by segment along the abscissa from left to right according to Figures 1 and 4. The red dotted lines illustrate the lower and upper limit of temperature variation (24.8 – 25.3 °C) in control water.

The silhouette outlines (Figure 6a) obtained from the mean temperature calculated based on data from each of the 55 columns on the abscissa (Figure 4) confirm conditioned water to be a very distinct physical state that extends to unprecedented distances. The difference in mean temperature ranged from 0.4-0.5 °C proximal to the cell surface and from 0.2-0.3 °C at mid distance. Following the structural consistency for three days, the original curve shapes, i.e. the difference in temperature between the two lines, remained unchanged at altered ambient temperatures (Figure 6b). On the second day of the experiment, the ambient temperature was lower (approximately 1.2 °C) than on the first and third days. The restricted IR emission observed in ordered water on the first day was confirmed by repeated measurements, as was its intrinsic effect on temperature. The physical state of ordered water was non-reversible and also consistent in darkness (not shown). Consequently, the consistency of the distance-related temperature curve shapes suggests that the restricted IR emission depends on a change in emissivity caused by stabilized coherent water with less thermal leakage independent of ambient temperature variation.

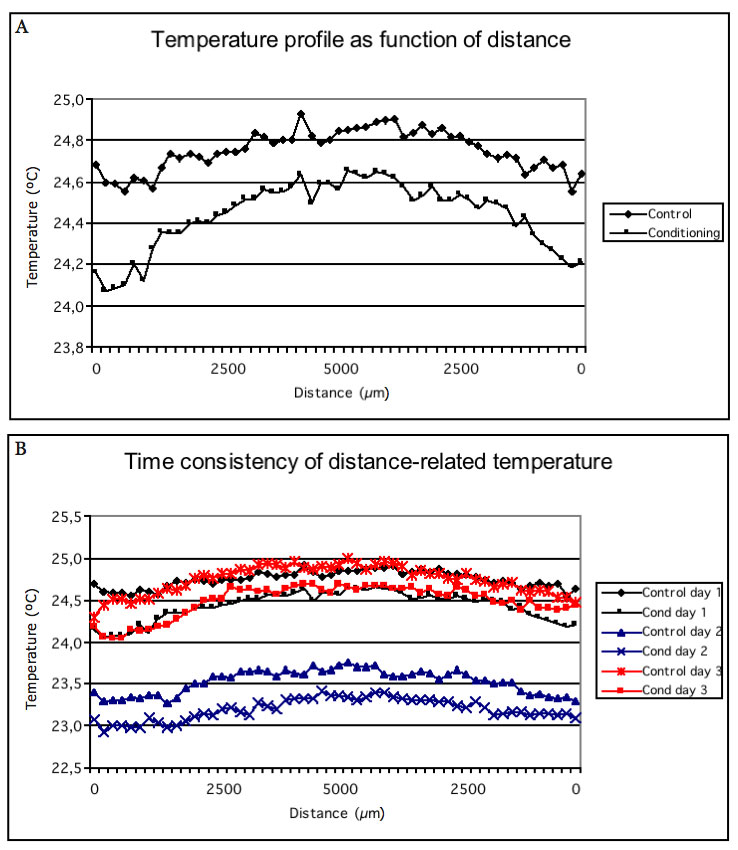
Figure 6: Temperature silhouette outlines as a function of distance from the cell wall surface (A) and the consistency (3 days) of long-range effects on the distance-related temperature (B). The cell surface is located at zero and the mid distance at 5000 µm on the abscissa. Mean temperature was calculated on 55 thermal IR numerical pixel data obtained column by column according to Figures 1 and 4.

Fractal Scaling in Thermal IR Emission and Temperature

The results of Fractal dimension and DFA analysis (Table 1) revealed a clear power law relationship of the thermal IR emission in conditioned water stored in quartz and polystyrene cells. The DFA value increased significantly (P<0.001) from 0.91 ± 0.02 (control) to 0.97 ± 0.02 (conditioning). A similar irregular trend series was obtained in polystyrene cells, 0.91 ± 0.01 (control) and 0.97 ± 0.01 (conditioning) (P<0.001). The DFA change indicates that the flickering of thermal IR emission is characterized by highly persistent long distance-attraction due to non-thermal interaction between the molecules of water. In coherent water domains the thermal fluctuation aligns with and unifies the magnetic field oscillations of freely movable electrons, which leads to long-range oscillation and structural stabilization among coherent clusters.

The fractal dimension obtained on thermal IR images at polar and non-polar interfacial surfaces indicates a difference in the long-range scaling behavior in ordered water. The mean value of FD in a hydrophilic environment was 1.442 ± 0.045 in control and 1.844 ± 0.008 in ordered distilled water, showing a significant difference (p<0.001) and a fairly ample interval. In hydrophobic conditions, the corresponding FD was 1.809 ± 0.013 and 1.784 ± 0.001, respectively (p<0.05). The fractal dimension provides an indication of the roughness in the thermal irregularity of the surface water. A higher fractal dimension equals a more detailed or smoother thermal irregularity. Hydrophobic storage conditions stimulated the fractal complexity of thermal IR flickering, which was notably unpeeled in ordered water.

Redoxpotential and pH

The redoxpotential and pH in control and conditioned distilled water are shown in Table 1. In the polar environment the ORP was 331 ± 3.3 mV (control) and 309 ± 1.9 mV (conditioning) (P<0.001) and pH 5.235 ± 0.030 (control) and 5.469 ± 0.088 (conditioning)(p<0.001). At non-polar conditions ORP was 311 ± 9.2 mV and 282 ± 4.3 mV (P<0.001) and pH 5.355 ± 0.018 and 5.534 ± 0.039 (p<0.001), respectively. The significant difference and reduction in ORP and the concomitant rise in pH show an elevated stock of free electrons from an existing coherent state of liquid water.

Discussion

The interaction among water molecules obeying mutual long-distance recognition and recalling dynamics reflects the self-organizing ability of a system that acts in a nonlinear regime (Del Giudice, 2006; Del Giudice and Tedeschi 2009). Distant attraction is present and produces an extended coherence of the fluctuations in the system (Froehlich, 1969; Del Giudice, 1985; Del Giudice, 1986). The long range ordering of water molecules, which ideally extends infinitely (Ling, 2003), suggests water as the source of a precedent electromagnetic field able to interact among distant molecules and adapt their oscillations to the level of excitation caused by the outcome of inherent chemical reactivity (Del Giudice, 1988; Del Giudice, 2006; Del Giudice and Tedeschi 2009). Several studies have demonstrated that interfacial water differs physically, thus governing long-term memory in a power-law fashion, in accordance with the formation of e.g. steep electrical gradients, shorter NMR-relaxation times, reduced IR emission and distinctive absorption of spectral ultraviolet, visible and infrared light (Zheng et al., 2006; Pollack, 2008; Chai et al. 2008). It is intriguing that less organized incident high entropy spectral light (Zheng et al., 2006; Pollack, 2008; Voeikov and Del Giudice, 2009) and sunlight (Yokono, 2009) are responsible for modulation and restructuring of the electrically charged low entropy ordered state of interfacial, surface (Zheng et al., 2006; Pollack, 2008; Voeikov and Del Giudice, 2009) and bulk volume water (Yokono, 2009). Irradiation by IR light or sunlight in the bulk volume of water at hydrophobic storage conditions induces a reversible change in the network of water molecules, gradually restoring the original structure (Yokono, 2009; Shimokawa, 2004). The temporary IR spectral changes represent a clathrate-like structural configuration at ambient conditions, which becomes considerably important as the water is super-cooled (Kanno, 2001) and this polyhedral structure is closely related to long-range ordering of water molecules (Shimokawa, 2004). Importantly, the formation of the clathrate-like structure was accessible in the hydrophobic environment of the vessel and thus demonstrates independency of hydrophilic surfaces.

In the present work, irradiation by the incident low entropy-ordered sunlight (Johansson, 2008a), irrespective of the presence of a hydrophilic or non-polar surface environment, the induction of structural ordering and elevated thickness of the ordered layer, leads to; i) a decrease in thermal IR emission from the sample surface, which is comparable to the entire size of the ordered surface zone of 10 x 10 mm2, ii) the significant decline in surface temperature of the ordered surface water comprising a structural configurative conformity that identifies a non-coherent to coherent state conversion (Huang et al., 2009; Voeikov and Del Giudice, 2009), where the intrinsic low entropy energy sustains a long-term nonlinear equilibrium distinctive state, iii) the allometric scaling behavior of the monofractal DFA exponent revealing a thermal fluctuation characterized by high persistence and long-range attraction between water molecules, iv) fractal dimension equally confirming the thermal IR activity of water as a genuine fractal characteristic (Taylor et al., 2005, Nittman and Stanley, 1987) following a significant fractal emergence in terms of the complexity in thermal fluctuation over several temperature scales in ordered water and v) the existence of stabilized coherent domains that enable a reservoir of quasi-free electrons measured as the sustained reduction in the redox-potential in the bulk volume of water, where the number of leaking electrons implies the tuned increase in pH.

According to classical theory, interfacial effects are anticipated to extend no more than nanometers from surfaces (Israelachvili, 1992), but previous observations imply repulsive interactions between surfaces and solutes up to several orders of magnitude further (Zheng and Pollack, 2003). Additionally, the present observations imply that not only interfacial surfaces are involved in long-range ordering, but the entire bulk volume of ordered water constitutes a power law sustained attraction when excited by low entropy sunlight.

According to the conjunction of a dissipative system (Froehlich, 1969; Celeghini et al., 1992), the exchange of energy and entropy with the environment relies on the fact that the absorption of spatially self-organized low entropy photons of incident sunlight is used to charge and displace the equilibrium towards a dominance of coherent domains. The structural alignment of the precedent high symmetry layer of structurally ordered water leads to an increased reservoir of quasi-free electrons. These electrons expand the LDL water state and can be released outwards either by modest excitations or by the quantum tunnel effect (Del Giudice and Tedeschi, 2009). Coherent water is a reducing element, and the reduction varies with the level to which the excited electrons reduce a sustained redox-potential that extends into the entire bulk volume of ordered water. Aligning the extraction of electrons from the coherent water domain leaves behind alkaline ionized molecules (hydroxyl ions), which reach the HDL fraction of water, supporting the rise in pH (Voeikov and Del Giudice, 2009). The self-trapped excited electrons of coherent domains are suggested shuttled as active hydrogen atoms or hydride ions when a proton gains an extra electron (Shirahata, 1997). As reported by Del Giudice and Tedeschi (2009), the ensemble of quasi-free electrons can produce cold vortices that have a quantified magnetic moment aligning them to ambient magnetic fields. Thus, the existence of coherent domains implies the presence of ordering magnetic fields in ordered water. Since the ordered water is colder, dependent on coherence, it cannot decay thermally; instead, its lifespan can extend for up to days or weeks (Del Giudice and Tedeschi, 2009; Elia, 2004).

The thermal IR emission intensity from water is a function of temperature and structure (Zheng et al., 2006). Because of the structural stability of coherent domains, the difference in emissivity therefore correlates with the considerably lower thermal IR emission compared to control water. The sustained and condensed temperature gradients with a consistently lowered magnitude in temperature for several days are proof of a remarkable stability of the excited states in ordered water that agrees with the consistency in increased pH of succussed water (Elia, 2004) and the distance-related decline in redox-potential of interfacial water (Zheng et al., 2006). Accumulated thermal IR emission implies the distribution into several concentric and condensed temperature zones to be aligned with the broadening temperature interval towards lowered temperatures in ordered water. The distinctiveness and sharpness in the spatial resolution of the condensed zones follow an acquisition of complex motion of coherent domains, indicating that the water state has a lowered mobility and stationary delimitation within the increment clustering of extended regions of coherent water. The sustained mixed gradient connecting interfacial and distant coherent water implies a pronounced attenuated thermal IR emission. Apparently, water molecules in the contiguous position of the mixed layer are substantially restricted and immobilized. The amplification of structural stability implies a local coordination of interfacial and distant molecular oscillations of coherent water.

The strong power law relationship in the fractal scaling boundary of the thermal IR emission flickering in ordered water obtained from the temperature data series and black and white images of pixel square areas is indicative of a high degree of self-similarity over multiple scales (Mandelbrot, 1983; West at al., 1997). The state of the underlying trend has a degree of autocorrelation, which is characterized by high persistence or long-term memory. The strong persistence in the DFA exponent indicates that the water temperature fluctuations from small temperature intervals to larger ones are positively correlated in a power-law fashion. Thus, a tendency towards decrease in water thermal IR emission is followed by another decrease in water IR emission at a different location related to fractal scaling behaviour. This implies that the long-range correlation should be considered an important factor in the trend prediction of water thermal IR emission. Additionally, the DFA exponent of water is strongly related to the capability of structural adaptation of the water body. Water with high DFA can maintain the fluctuation tendency of thermal radiation even when the external temperature changes, producing a decrease of entropy of the system and giving rise to potential self-organization (Del Giudice E, Tedeschi, 2009).

The significant relationship between an ample detailed irregularity and the fractal dimension indicates that the particular fractal structure may be part of the basis of the ordering state (Vitiello, 2009a; Vitiello, 2009b; Blasone et al., 2011). Studies that attempt to identify the physical principles underlying the formation of real snowflakes and pose questions in relation to snowflake growth, such as the identical six arm morphology and the overall dendritic pattern of each arm resembling the other five, have demonstrated fractal properties of real snowflakes (Nittman and Stanley, 1987). Typical growth patterns showed that real snowflakes are fractal objects, as is the thermal IR flickering of the coherent state in water. The fractal dimension (FD 1.4-2.0) was independent of the cluster mass but dependent on a non-linearity parameter (η) that tunes the balance between tip and fjord growth (decreasing (η) from 1.0 to 0.05), resembling a huge range of experimentally observed branching patterns. Thus, the increase in fractal dimension in ordered water is comparable to the diversity of dendritic growth in snowflakes, which implies that scaling geometry is a part of structural ordering in both the liquid and the ice state of water. Notably, the connection to distant hydrophobic surfaces, an ordinary feature of bio-systems, stimulates the fractal scaling diversity of water.

Furthermore, fractals frequently found in natural environments (e.g. water or hill scenery, clouds, waves, blood vessels, electrical charge, etc.) have FD values in the range of 1.3-1.8 (Kaplan and Kaplan, 1982; Purcell and Lamb, 1984; Taylor et al., 2005) and it has been suggested that people’s highest aesthetic preference for natural scenery is in the range of 1.3-1.5 (Hagerhal et al., 2004), with its maximum set at 1.3 (Arks, 1996), which in humans implies induction of a restorative response in physiological and cognitive functions leading to a wakeful relaxed state associated with external focus, attention and alertness (Hagerhal et al., 2008; Ward, 2003). These observations correlate with the long-term memory of the DFA exponent in adaptive physiological homeostasis demonstrated by ingestion of functional water in healthy humans (Johansson, 2008b). The improvement in fractal heart rhythm dynamics was associated with a rapid parasympathetic restorative response from the heart with a tentative stabilizing effect on normal blood pressure, less blood pressure variability and stimulating mucosal humoral immunity (Johansson, 2009). It should be noted that in the present study, i) the fractal dimension of the thermal IR emission flickering of ordinary water correlates strongly with the FD value in humans viewing their aesthetic naturalness preference, ii) that the emergence complexity of fractal dimension of the coherent state of water agrees with the FD value of real snowflakes and biological structural architecture (Hagerhal et al., 2008) and iii) that the fractal scaling geometry is a part of structural ordering in coherent water (Vitiello, 2009a; Vitiello, 2009b; Blasone et al., 2011).

Conclusions

An organized highly stable coherent structure of bulk liquid water forms on irradiation in the presence of low entropy sunlight at room temperature, characterized by persistent fractal long distance-attraction based on self-organization ability. Reduction in thermal IR emission tunes a significant decline in surface temperature and aligns structural conformity. A distinctive configurative coherent aqueous state reveals a fractal scaling relationship in temperature fluctuations that maintains a self-organized structural adaptation irrespective of ambient temperature. In coherent water, the fractal constitution reveals a tentative high aesthetic preference in the human perception of naturalness, resembling the fractal nature of real snowflakes, structural architecture of biological structures and restoration of human physiological and cognitive functions, as well as the fact that mimic geometry of natural objects is part of coherent water ordering.

References

Arks DJ, Spott JC. Quantifying aesthetic preference for chaotic patterns. J Empir Stud Arts (1996). 4, 1-16.

Asp N-G. Health effects of probiotic and preprobiotic foods (2001). Scand J Nutr 45, 57.

Blasone M, Vitiello G, Jizba P. Quantum field theory and its macroscopic manifestations (2011). Imperial College Press, London. Chapter 1.9: 26-30.

Banerjee D, Bhat SN, Bhat SV, Leporini D. ESR evidence for 2 coexisting liquid phases in deeply super-cooled water (2009). PNAS 106, 11448-11453.

Biondini M. Allometric scaling laws for water uptake by plant roots (2008). J Theor Biol 251, 35-59.

Chai BH, Zheng J-M Zhao Q, Pollack GH. Spectroscopic studies of solutes in aqueous solution (2008). J Phys Chem 112, 2242-2247.

Daudert B, Lapidus ML. Localization on snowflake domains (2007). Fractals 15, 255-272.

Celeghini E, Rasetti M, Vitiello G. Quantum dissipation (1992). Ann Phys 215, 156-170.

Del Giudice E, Doglia S, Milani M, Vitiello G. A quantum field theoretical approach to the collective behaviour of biological systems (1985). Nucl Phys B251 (FS13) 375-400.

Del Giudice E, Doglia S, Milani M, Vitiello G. Electromagnetic field and spontaneous symmetry breaking in biological matter (1986). Nucl Phys B275 (FS17) 185-199.

Del Giudice E, Preparata G, Vitiello G. Water as a free electric dipole laser (1988). Phys Rev Letters 61, 1085-1088.

Del Giudice E and Vitiello G. Role of the electromagnetic field in the formation of domains in the process of symmetry-breaking phase transitions (2006). Phys Rev A 74, 022105-1-9.

Del Giudice E. Formation of dissipative structures in liquid water (2009). Water 2, Suppl. 1, 14-15.

Del Giudice E, Tedeschi A. Water and autocatalysis in living matter (2009). Electromag Biol Med 28, 46-52.

Derjaguin BV, Churaev NV, Muller VM (1987). Surface forces. Consultants Bureau, New York, Chapter 7: 231-426.

Diplock AT, Aggett PJ, Ashwell M, Bornet F, Fern EB, Roberfroid MB. Scientific concepts of functional foods in Europe: Consensus document (1999). Br J Nutr 1, 81, S1- S27.

Domrachev A, Roldigin GA, Selivanovsky DA. Rule of sound and liquid water a dnamically unstable polymeric system in mechano-chemically activated processes of oxygen production on earth (1992). J Phys Chem 66, 851-855.

Elia V, Napoli E. New physico-chemical properties of extremely diluted aqueous solutions (2004). J Therm Anal Calorim 75, 815-836.

Froehlich H (1969). Theoretical physics and biology. In: Proceedings of the first international conference on theoretical physics and biology. Marios M ed. Versailes Amsterdam, Holland: 12-22.

Gileadi, Kirowa-Eisner E, Penciner J (1975). Interfacial electrochemistry. An experimental approach. Reading, Mass. Addison-Wesley: 368-375.

Hagerhal CM, Laike T, Taylor RP, Küller M, Küller R, Martin TP. Investigations of human EEG response to viewing fractal patterns (2008). Perception 37, 1488-1494.

Hagerhal CM, Purcell T, Taylor R. Fractal dimension of landscape silhouette as a predictor of landscape preference (2004). J Environm Psychol 24;247-255.

Huang C, Wikfeldt, KT, Tokushima T, Nordlund D, Harada Y, Bergmann U, Niebuhr M, Weiss TM. Horikawa Y, Leetmaa M, Ljungberg MP, Takahashi O, Lenz A, Ojamäe L, Lyubartsev AP, Shin S, Pettersson LGM, Nilsson A (2009). The inhomogeneous structure of water. PNAS 106, 15214-15218.

Huang Z-W, Liu C-Q, Shi K. Monofractal and multifractal scaling analysis of pH time series from Dongting lake inlet and outlet (2010). Fractals 18, 309-317.

Ikeda S, Takata T, Komoda M, Hara M, Kondo JN, Domen K, Tanaka A, Hosono H, Kawazoe H. Mechano-catalysis a novel method for over-all water splitting (1999). Phys Chem Chem Phys 1, 4485-4491.

Israelachvili J (1992). Intermolecular and surface forces. San Diego, Academic press, 282-287.

Johansson B (2008a). Synchronized water and production thereof. (patent application, PCT/SE000119. February 13.

Johansson B (2008b). Synkront vatten. Egenskaper och effekter i anfuktad luft, vatten och biologiska miljöer. Akloma Bioscence AB, Medeon Science Park, 205 12 Malmö, Sweden. ISBN 978-9-6-050. email: info@akloma.com: 13-73.

Johansson B. Effects of functional water on heart rate, heart rate variability, and salivary immunoglobulin A in healthy humans: a pilot study (2009). J Alter Compl Med 15, 871-877.

Kanno H, Yokoyama H, Yoshimura Y. A new interpretation of anomalous properties of water based on Stillinger´s postulate (2001). J Phys Chem B 105, 2019-2026.

Kaplan R, Kaplan S (1982). Cognition and environment: Functioning in an uncertain world. New York, Praeger: 73-116.

Ling GN. A new theoretical foundation for the polarized-orientated multilayer theory of cell water and for inanimate systems demonstrating long-range dynamic structuring of water (2003). Physol Chem Phys Med NMR 35, 90-130.

Luo J, Tang J, Heng B. The fractal dimension estimate of water tree in XLPE dielectric (2003). IEEE Xplore 23-25 September; 177-179.

Mallamace F, Corsaro C, Broccio M, Branca C, Gonzalez-Segredo N, Spooren J, Chen S-H, Stanley HE. NMR evidence of a sharp change in measure of local order in deeply super-cooled confined water (2008). PNAS 105, 12725-12729.

Mallamace F. The liquid water polymorphism (2009). PNAS 106, 15097-15098.

Mandelbrot B (1983). The fractal geometry of nature. NewYork. W.H. Freeman and Company: 1-20.

Modig K, Pfrommer BG, Halle B. Temperature-dependent hydrogen-bond geometry in liquid water (2003). Phys Rev Lett 90, 075502-1-075502-4.

Nittman J, Stanley H.E. Non-deterministic approach to anisotropic growth pattern with continuously tunable morphology. The fractal properties of some real snowflakes (1987). J phys A Math Gen 20, L1185-L1191.

Peng CK, Buldyrev SV, Havlin S, Simons M, Stanley HE, Goldberger AL. Mosaic organization of DNA nucleotides (1994). Phys Rev E 49, 1685-1689.

Pollack GH. Long-range water structuring at hydrophilic surfaces. Third annual conference on the physics, chemistry and biology of water 2008. Vermont, US.

Pollack GH. The secret life of water E – H2O. Fifth international workshop on natural energies (2011). Höör, Sweden.
Prigogine I, Nicolis G (1977). Selforganisation in non-equilibrium systems, from dissipative structures to order through fluctuations. Wiley, New York: 90-160.

Purcell T, Lamb RJ. Landscape perception: An examination and empirical investigation of the two central issues in the area (1984). J Environm Manage 19, 31-63.

Shimokawa S, Yokono T, Mizuno T, Tamura H. Erata T, Araio T. Effect of far-infrared light irradiation on water observed by X-ray diffraction measurements (2004) Appl Phys 43, L545-L547.

Shirahata S, kabayama S, Nakano M, Miuta T, Kusumoto K, Gotoh M, Hayashi H, Otsubo K, Morisawa S, Katakura Y. Electrolyzed-reduced water scavenges active oxygen species and protects DNA from oxidative damage (1997). Biochem Biophys Res Com 234, 268-274.

Taylor RP, Spehar B, Wise JA, Clifford CWG, Newell BR, Hagerhall CM, Purcell T, Martin TP. Perceptual and physiological responses to the visual complexity of fractal patterns (2005). Nonlin Dynam Psychol Life Sci 9, 89-112.

Turning M (1952). The chemical basis of morphogenesis. 237: 37-72.

Vitiello G. Current states, fractals and brain waves (2009a). New Math Natural Comp. 5, 245-264.

Vitiello G (2009b). Fractals and the Fock-Bargmann representation of coherent states. Third international representation of coherent states (QI-2009). Lecture notes in artificial intelligence edited by Goebel et al. In: Quantum Interaction. Bruza P et al. Eds. Springer-Verlag, Berlin, Heidelberg: 6-16.

Voeikov VL, DelGiudice E. Water respiration–the basis of the living state (2009). Water 1, 52-75.

Ward LM. Synchronous neural oscillations and cognitive processes (2003). Trends in Cogn Sci 7, 553-59.

Wernet Ph, Nordlund D, Bergman U, Cavalleri M, Odelius M, Ogasawara H, Näslund LÅ, Hirsch TK, Ojamäe L, Glatzel LG, Pettersson LGM, Nilsson A. The structure of the first coordination shell in liquid water (2004). Science 304, 995-998.

West GB, Brown JH, Enquist BJ. A general model for the origin of allometric scaling laws in biology (1997). Science 276, 122-126.

Wiggins PM. Enzymes and two types of water (2002). J Biol Phys Chem 2, 25-37.

Yokono T, Shimokawa S, Yokono m, Hattori H. Infrared spectroscopic study of structural change of liquid water induced by sunlight irradiation (2009). Water 1, 29-34.

Zheng J-M, Chin W-C, Khijniak E, Khijniak Jr E, Pollack GH. Surfaces and interfacial water. Evidence that hydrophilic surfaces have long-range impact (2006). Adv Coll Interf Sci 127, 19-27.

Zheng J-M, Pollack GH. Long range forces from polymer surfaces (2003). Phys Rev 68, 031408.

Web References

1. Chaplin M. Water structure and science. http://www.btinternet.com/~martin.chaplin/index.html [2010]

2. Calculation of Fractal Dimension FD was enabled by a commercial software Benoit 1.3. The software was downloaded on www.trusoft-international.com/benoit.html [2010]

3. Goldberger AL. Fractal dynamics in physiology. Alterations with disease and aging (2002). PNAS 99, 2466-2472. Software for calculation of DFA was downloaded from www.physionet.org/physiotools/dfa [2009]

Discussion with Reviewers

Anonymous Reviewer: What is exactly the topographic geometrical matrix (TGM) and how does it work? What is the state of “highly ordered photons”? How is it described in QED? In quantum optics and in QED the laser is a state of coherent light. What is the relation of “highly ordered photons” with laser light?

B. Johansson & S. Sukhotskaya: The TGM is a transparent matrix raster that consists of a topographic fractal geometrical field structure graphically imprinted by silver ink on a polyethyleneterephtalate substrate. The structural design is based on the geometry of the concentric circle, wherein there must be a specific relationship in accordance with the proportion of Phi (1.68) or Fibonacci’s sequence of numbers between the outer diameter of the circle and the next circle, counting inwards towards the common centre of the circles. The line widths constituting the geometrical matrix equally follow the proportion of Phi.

The TGM works as a fractal spatial-wave “Fourier raster” capable of transforming the spatial dissonance of electromagnetic field oscillations into harmonic wave components. Incident light that transmits the raster activates the fractal field due to the interference of the fluxes transmitted through and reflected by the diffraction lattice of the fractal geometry. The distorted peak field abnormalities are thus corrected efficiently and spatial structural characteristics of the light fields improved.

Studies on spectral light at the 634 nm wavelength evaluated from images of transmitted and captured TGM conditioned light showed a substantial reduction in entropy, a change in fractal dimension towards the Mandelbrot algorithm and increased intensity. In terms of optics, while uniformly passing through space, the radiation undergoes rearrangement by the diffraction lattice and transforms into a nonlinear series of wave structures, with alternating maximums of increased intensity.

According to QED, the photons of coherent light (lasers) act together as a unit, produced by stimulated emission from a single atom and are monochromatic in appearance. The highly ordered TGM conditioning photons are ordinary light at different frequencies emitted from individual atoms that are reorganized virtually according to fractal wave dynamics in space passing the TGM matrix.

Reviewer: What is the role of H-bonds in the experiment? Are they the cause of water ordering? Are they the effect of the ordering induced by the “highly ordered photons”? How these ordered photons produce ordering in the water?

Johansson & Sukhotskaya: The condition of coherent water is described as a low-entropy highly ordered state, where the molecules have their lowest energy position close to that of tetrahedrally connected crystalline ice, coordinating four hydrogen bonds. Because tetrahedral species do not support thermal vibrations at ambient temperature, the structure is more or less unaffected by increasing temperature. In our studies, a similar sustained stability of the water structure was identified irrespective of small variations in external temperature, which supports a tetrahedral structuring of water molecules.

Besides a shift in the thermal emission in water from lower to higher wavelengths comprising a reduced outflow of thermal energy in line with the cooling effect, the fractal behaviour in thermal IR flickering reveals president long distance coordination among water molecules. Thus, the fractal constitution of highly ordered photons of incident light may have the exact quality of structural energy to interact and tune with an electromagnetic field that makes water molecules oscillate in unison in the spatial region of expanding coherent clusters. The reduced energy of a ground state where all species oscillate at a unifying phase implies that the photons are trapped and cannot be irradiated externally, thus increasing the sustainability of coherent domains. The coupled oscillations of the thermal IR fluctuations and those of the self-trapped magnetic field are associated with negative charged hydrogen that corresponds with strong hydrogen bonds, which extend the volume and/or the number of coherent clusters comprising the entire volume of water.

Reviewer: In the paper there is mention of Coherent Domains and of Pollack’s ordered water state. According to the authors, are these water states similar states? Which one are the differences between them, if any?

Johansson & Sukhotskaya: From our perspective and observations there are similarities but also differences between the two states. According to the exclusion zone of water defined by Pollack, which mimics interfacial water, this water depends on external polar surfaces or surface water, not necessarily implied by the Coherent Domains. Our studies indicate that the sustainable fractal ordered state exists equally in a hydrophilic and a hydrophobic environment and is stimulated at hydrophobic conditions. Similarly, a structural but reversible change of the liquid water state was induced by ordinary sunlight in a hydrophobic environment (Shimokawa et al., 2009). Additionally, in our experiment at hydrophilic conditions, the temperature in the interfacial zone was significantly decreased compared to that of the bulk water, which indicates the presence of two different forces that amplify each other within the limitation of the interfacial zone.

Reviewer: Why was the pH value of control water in quartz so low? Such acidity is not characteristic for distilled water. Indeed pH of control water in polystyrene was much higher. Besides pH value of conditioned water in quartz increased by more then 2 units — that’s a lot! On the other hand though the redox potential value in conditioned water in quartz was lower then in control water, it decreased much less then it should in relation to pH elevation. According to Nernst equation, when pH in water increases by 1 unit, redox potential should decrease by 59 mV. So if your data is not related to some artifacts (for example, impurities) electron donating capacity of conditioned water is lower (relatively to pH) then that of control water.

Johansson & Sukhotskaya: This is an interesting observation. We have discussed the deviation in the mean control pH value from different viewpoints. Importantly, the deviation in pH was observed in control distilled water stored in hydrophilic beakers, the only sample of the four different conditions without stimulated fractal ordering of distilled water. Thus, the other three water conditions align with a fractal structural conformity. Our pH measurements showed the distilled control water in quartz beakers to be much lower than expected. This can be seen from the corresponding higher standard deviation of the control water (Table 1; the mean pH value was corrected in the final version of the manuscript).

Continued pH measurements of control water in quartz beakers showed that approximately 20 % of the water samples were lower compared to expected pH values. The lowered control waters were also checked by pH-indicator strips (Merck Acilit pH 0-6) not found to deviate from expected values (pH 5.0-5.5).

According to the pH measurements from Pollack’s studies on exclusion zone water, the pH follows a hyperbolic curve shape with the lowest pH values close to and the highest pH values distant from the hydrophilic surface. The formation of pH gradients showed pH separation, where the pH sensitive dyes indicate a pH between 3 and 4 in the interfacial zone. Due to accumulation of electrons and protons in the coherent domains they have a high reductive and acidic capacity that governs a lowered pH. The electrons could be captured by oxygen atoms, giving rise to hydroxyl ions forced out of the coherent compartments because of a non-coherent oscillation, thus increasing the pH among ordinary water molecules (Voeikov and DelGiudice, 2009). It is also known that the volume of the beaker in which the measurement was performed affects the width of the exclusion zone. Higher volumes generate expanding and distant exclusion zones (Pollack, 2011).

In our experimental set up, the pH electrode was centred in a beaker with the tip 2 cm below the water surface and 2 cm above the bottom of the beaker. The pH electrode was made from high quality quartz glass, 11-6 mm in diameter with a tapered cone-like tip, which made the surface a strong hydrophilic attractor. The narrow glass membrane of the electrode was a high-purity grade sintered porous material with a high hydrophilic square surface that has an extremely high capacity to accumulate and cross-link coherent water clusters. Since the pH measurements were conducted in 30 ml beakers, a broadening of the interfacial water zone could be expected compared with the 1 square cm cell of the thermal IR experiment.

Thermal IR imaging of the surface water revealed a complex array of concentric temperature gradients around the pH electrode. The IR image visualised a higher structural organisation close to the surface of the electrode, extending into the bulk water and indicating a low temperature zone with lowered pH. The pH separation close to the sintered membrane of the electrode provided a tentative intermittent nucleation site for local attraction and growth of coherent water clusters with temporary accumulation of protons, thus decreasing the pH in the distilled water close to the membrane.

Due to the non-uniform distribution of protons and the local shift in the pH of distilled control water stored in quartz beakers, a correction of the mean pH value has been made in Table 1.